深孔台阶爆破近远区振动特征的试验研究
2017-04-20辛崇伟梁书锋刘殿书
韩 亮, 辛崇伟, 梁书锋, 刘殿书
(1. 华北科技学院 安全工程学院,北京 101601; 2. 北京科技大学 土木与资源工程学院, 北京 100083;3. 中国矿业大学(北京) 力学与建筑工程学院, 北京 100083)
深孔台阶爆破近远区振动特征的试验研究
韩 亮1, 辛崇伟2, 梁书锋3, 刘殿书3
(1. 华北科技学院 安全工程学院,北京 101601; 2. 北京科技大学 土木与资源工程学院, 北京 100083;3. 中国矿业大学(北京) 力学与建筑工程学院, 北京 100083)
为了探索深孔台阶爆破在近区和远区的振动特征,以现场试验为基础,利用回归分析、随机分析及小波包分解技术,从爆破振动信号的衰减规律、三分量特征、随机特征及能量分布等方面对二者进行了对比研究,结果显示:振速三分量在近区的K、α值均大于远区,远区各分量的α值更为接近。振速三分量在远区的相关系数大于近区,且更接近1,三分量中垂向分量的相关系数最大。近区当比例距离小于5时,径向振速最大,比例距离大于等于5时,垂向振速最大。远区的垂向振速最大。无论在近区还是远区,切向振速一般最小。振速三分量在近区的变异系数大于远区,径向振速的变异系数在近区和远区较为接近。最大段药量或爆心距增加时,近区及远区的能量均向低频带流动,近区的移动速度更快,同时近区及远区能量分布的频带宽度也将趋于集中,近区的频带宽度更宽。
深孔爆破; 近区; 回归分析; 衰减规律; 随机变量; 能量分布; 小波包
深孔台阶爆破是矿山、岩土工程生产作业的主要方式,然而爆破带来的震动效应也极大影响了周边建筑设施的安全及边坡稳定。工程中通常采用萨道夫斯基公式估算测点的振动强度,受群孔效应的影响,在爆破地震波作用区域,近区和远区的预测误差相差较大。
近区和远区可通过比例药量ρ或者比例距离SD来界定,文献[1]给出的深孔台阶爆破近区范围ρ在0.24~0.87之间,中远区ρ在0.08~0.312之间;文献[2]以振速衰减曲线的斜率为指标,当斜率小于-5时为近区,大于-5为中远区;文献[3]建议将比例距离SD等于10作为近区和远区的分界。上述定义仅考虑了振速衰减规律的异同,并未对爆破振动的其他特征进行分析和比较。此外,爆破近区和远区属于特定条件和场地下的相对区域,即便通过统计得到的分布范围,也很难推广至其他工程。因此,对于指导工程实践而言,了解二者在各自范围内的振动特征比范围定义更有意义。
目前,国内外关于这方面的研究尚不多见,本文依托深孔台阶爆破现场工程,以大量实测数据为基础,拟从衰减规律、三分量特征、随机特征、能量分布等方面,揭示近区和远区的主要振动特征,研究成果对深孔台阶爆破具有积极的指导意义。
1 爆破振动测试
1.1 测试方案及爆破参数
(1) 测试方案
试验场地位于北京水泥厂有限责任公司凤山矿,由于监测目的不同,近区与远区的爆破振动测试分别位于两个采场,采场平整,地质条件相差不大。试验中,以单段最大药量、最大段群孔爆心距作为参数,计算出各测点的比例距离,以此作为近、远区的度量。测线沿爆心布置,约4~10个测点,间距10~30 m,所有测点均布置在爆区上平台后方。近区测试位于测区Ⅰ,单段药量为1 000~2 000 kg,爆区后方首个测点控制在距爆区40~50 m;远区测试位于测区Ⅱ,单段药量为130~500 kg,首个测点位于爆区后方200~500 m,见图1。
(2) 爆破参数
测区Ⅰ与测区Ⅱ爆破参数基本相同,如表1所示。

(a)

(b)

表1 现场爆破参数表
1.2 振动衰减规律
测区Ⅰ与测区Ⅱ分别测得有效数据77组和122组[4],进行非线性回归处理,可得爆破近区与远区水平径向、水平切向及垂直向振速衰减规律与回归曲线,见图2和3。
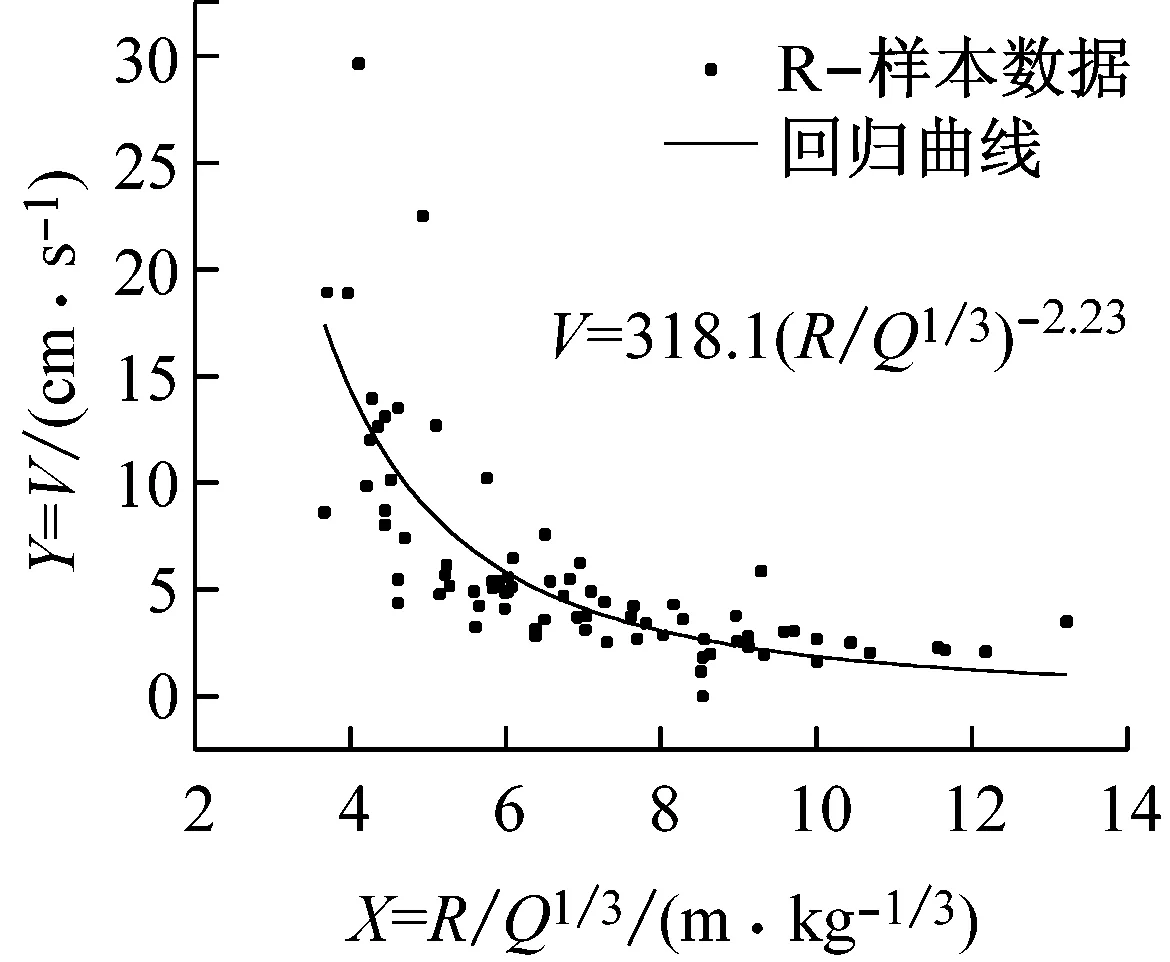
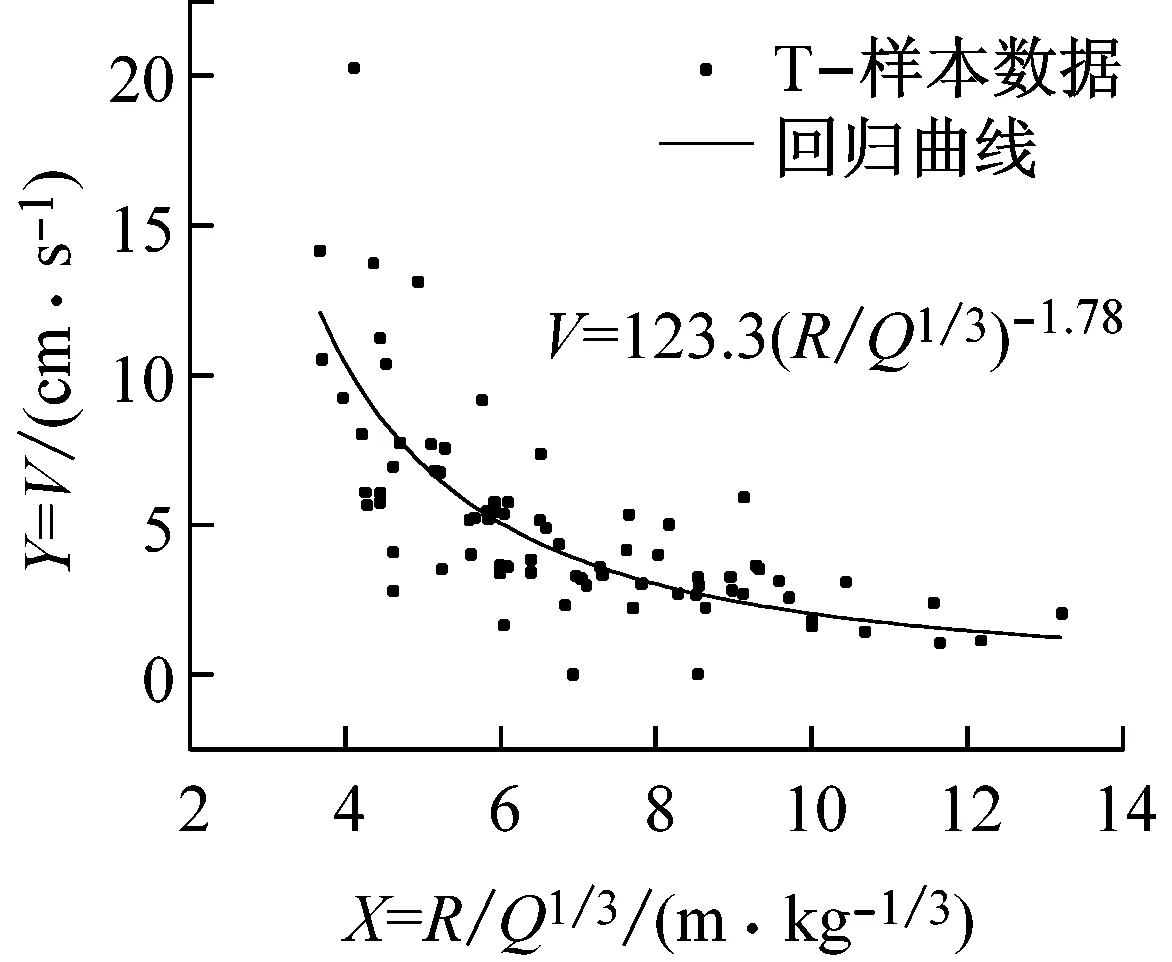
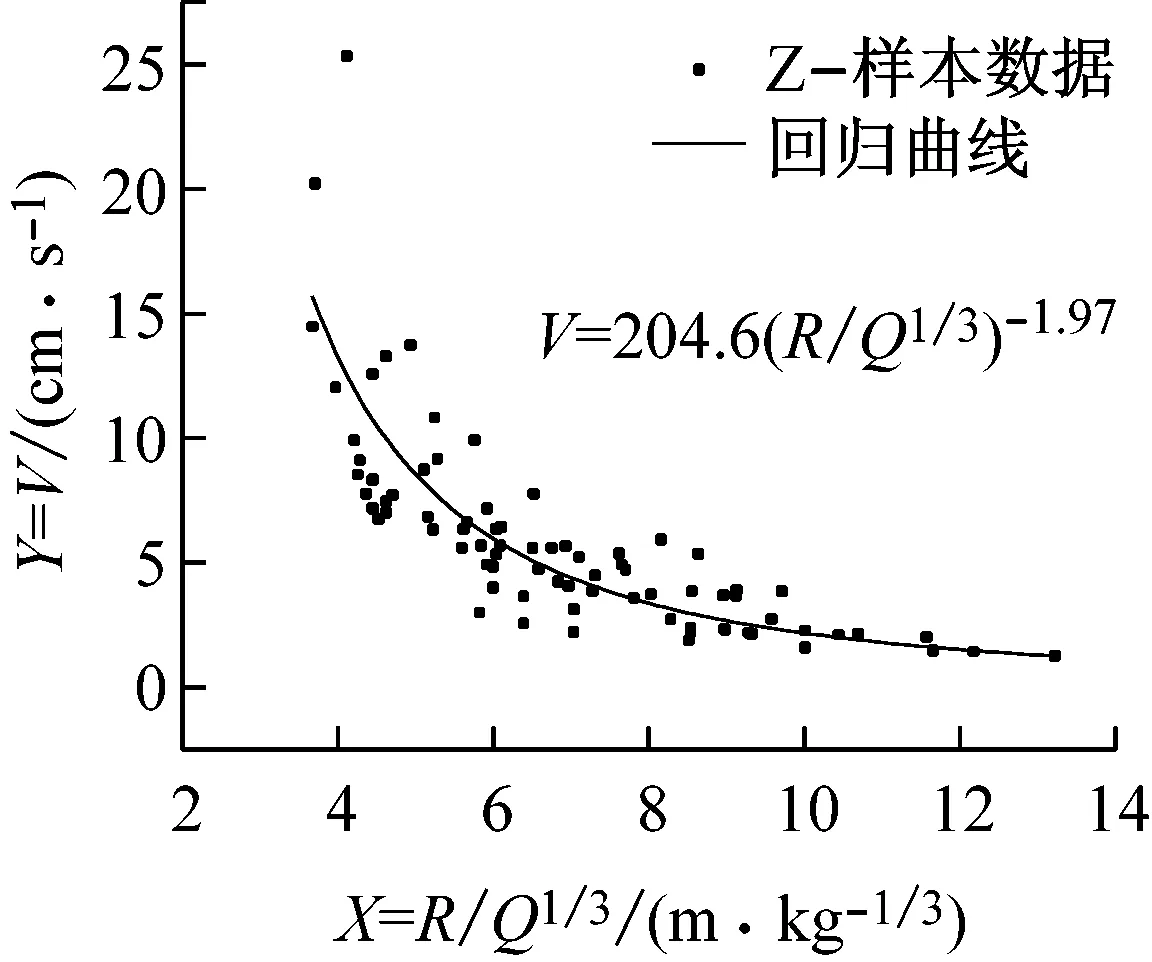
图2 近区水平径向、切向、垂向振速回归曲线
将回归计算得到的爆破振动衰减参数K和α值列于表2中。由表2可见,爆破近区中水平径向、切向和垂向的K、α值均大于远区。表明爆源爆炸后,震动波经传播路径衰减后在近区的剩余爆破能量要大于远区,同时衰减速度也大于远区。相对于近区而言,振速三分量的α值在远区更为接近,表明远区的振速衰减已趋于稳定,而近区因受多种爆破条件及群孔效应的影响,振速三分量的衰减速度相差较大。



图3 远区水平径向、切向、垂向振速回归曲线

表2 三方向K、α值比较
将非线性回归的评价指标相关系数列于表3中。

表3 三方向相关系数比较
由表3可见,远区振速三分量的相关系数大于近区,且更接近1,而无论在近区还是远区,垂向分量的相关系数均为最大。表明远区观测数据在回归拟合时的规律性要强于近区,同时垂向振速具有更加明晰的方向性,因此,在后续研究中,主要针对垂向分量展开。
2 振速三分量的对比研究
将图2和3中近区和远区的观测值及三分量回归曲线分别绘于图4中。由图4可知,在爆破近区,当比例距离SD<5时,大部分测点的水平径向振速大于垂向振速;当比例距离SD≥5时,大部分测点的垂向振速大于水平径向振速。水平切向振速一般最小。在爆破远区,大部分测点的垂向振速大于水平径向和切向振速。
根据前人研究[5],在爆源距离为15倍孔深范围内,水平径向振速大于垂向振速。由于试验现场为深孔台阶爆破,炮孔均为柱状药包而非球形药包。在爆破近区,群孔同时爆破产生的爆破震动波仍有柱状波阵面的特点,而柱面波在水平径向的振动速度最大。随着传播距离的增大,柱状波阵面的特点逐渐减弱,群孔爆源才可看做点爆源,因此,爆破远区垂向振速最大。在水平方向上,切向分量通常小于径向分量。

(a)

(b)
3 振速幅值的随机特征
振动观测中,爆破条件、药量、爆心距及衰减系数共同决定了爆破振动幅值的大小。在同一块场地,相同爆破条件下,每一次观测点距爆心的比例距离一致,得到的爆破地震波幅值均不相同,因此,可以认为在上述条件下观测的爆破振动幅值具备随机变量的特征。
假设在爆破近区,同一比例距离处进行了N次爆破振动观测试验,得到了N个爆破振动幅值Vi,其中(i=1,2,3,…,N);同样在爆破远区也进行了N次这样的观测试验,得到的N个振动幅值为Ui,(i=1,2,3,…,N)。
根据随机变量的分布特点,则有
(1)
(2)
上述正态分布的概率密度参数中,μ和σ2均为未知量,因此只能用样本值Vi和Ui对σ2进行估计。样本分析时分别选取了近似同一的比例距离(近区为SD=6,远区为SD=40)下的13组振动观测数据,见表4。
由概率论知识可知,修正样本方差S*2是总体方差σ2的无偏估计量。因此可以利用S*2对总体方差σ2进行估计。

表4 相同比例距离下爆破近区和远区振动观测数据
根据修正样本标准差定义,有:
(3)
式中:n为样本数;xi为样本数据;x为样本均值。
由于近区和远区的振速不在同一数量级,上式得到的修正样本标准差仅为绝对指标,需对其进一步处理,并用变异系数来表征随机变量的偏差程度。
变异系数的计算,如下式,
(4)
式中:CV为变异系数;x为样本均值。
计算结果见表5。由表5可知,近区振速三分量的变异系数均大于远区,表明近区条件下对振速的影响更为复杂,存在若干未知因素影响着爆破振动的随机性。同时,三分量中,径向振速的变异系数在近区和远区较为接近,表明本试验中,径向振速受未知因素的影响最小。

表5 爆破近区与远区振速变异系数
4 不同爆破条件下能量的分布特征
4.1 振动信号的小波包分析
爆破地震波的产生、传播以及对建筑物影响的过程,其本质是能量在不同介质中传递和转移的过程。根据先前学者研究,同一爆破场地下,最大段药量和爆心距[6-7]对能量的分布和衰减影响最大。因此,基于近区和远区的实测波形,以小波包分析技术为研究手段,分析并比较最大段药量和爆心距这两个条件对能量在近区及远区分布和衰减的影响。
通过试算,选取sym8为最优小波基,采样频率为8 000 Hz,小波包分解尺度为9。频带宽度依次为:0~7.812 5 Hz、7.812 5~15.625 Hz、15.625~23.437 5 Hz、…、3 992.187 5~4 000 Hz。由于爆破信号在高频分布较少,这里只对第1~19频带的能量分布进行研究,即0~148.437 5 Hz的频带范围。
4.2 最大段药量对近远区能量分布的影响
在近区及远区波形文件中,分别选择爆心距一定,最大段药量依次增大的样本进行小波包分解。样本情况见表6。得到不同最大段药量下,近区和远区各频带能量的分布情况,此处仅列举第1~19频带,下同。见图5。

表6 样本概况

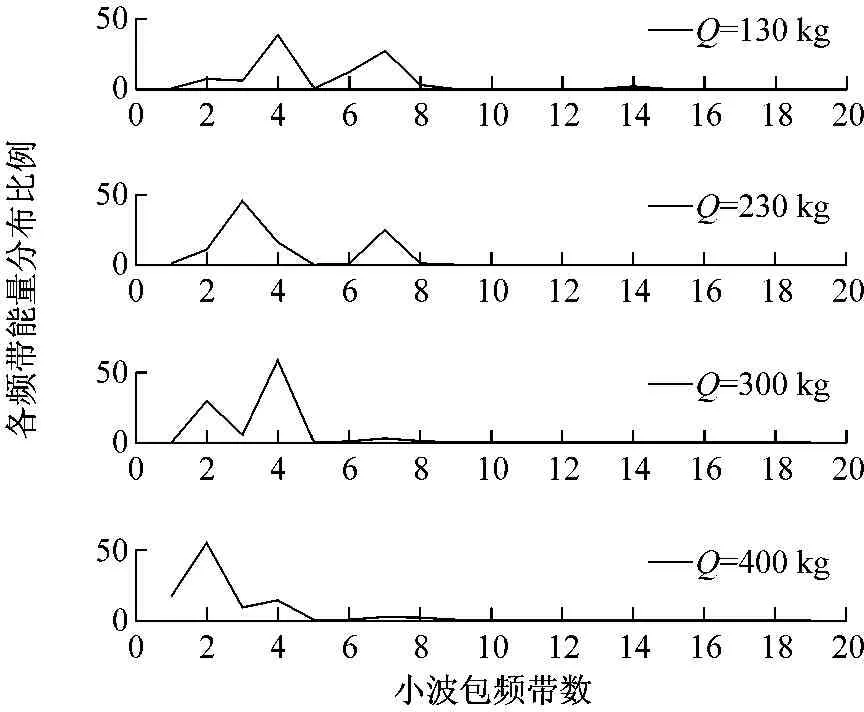
(a) 近区
通过图5,可得到如下结论:
(1) 最大段药量增加时,近区及远区各测点的低频带能量所占比例随之上升,高频带能量所占比例逐渐下降,能量随最大段药量的增加向低频流动,且近区的流动速度更快。
(2) 最大段药量较小时,近区及远区能量在1~9频带均有分布,且近区的分布宽度较大;随着最大段药量的增加,能量分布趋于低频,近区分布宽度仍大于远区。由于低频接近建筑物的自振频率,因此,最大段药量的增加将给周边建筑物安全带来极大的影响。
4.3 爆心距对近远区能量分布的影响
在近区及远区波形文件中,分别选择最大段药量一定,爆心距依次增大的样本进行小波包分解。样本情况见表7。得到不同爆心距下,近区和远区各频带能量的分布情况,见图6。
通过图6,可得到如下结论:

表7 样本概况
(1) 爆心距增大时,近区及远区各测点的低频带能量所占比例随之上升,高频带能量所占比例逐渐下降,能量随爆心距的增加向低频流动,且近区的流动速度更快。
(2) 爆心距较小时,近区及远区能量在各个频带均有分布,分布范围较宽,且近区的分布宽度较大;随着爆心距的增加,能量分布趋于低频,相对而言,远区能量在低频带的集中程度更高。虽然能量随着爆心距的增加在不断衰减,但由于低频能量的集中,将越来越接近建筑物的自然频率,同样对周边建筑物有较大影响。

(a) 近区

(b) 远区
5 结 论
本文以现场试验为基础,利用回归分析、随机分析及小波包分解技术,从爆破振动信号的衰减规律、三分量特征、随机特征及能量分布等方面,对本例中深孔台阶爆破近区和远区的振动特征进行了对比研究,主要结论如下:
(1) 振速三分量在近区的K、α值均大于远区,远区各分量的α值更为接近。振速三分量在远区的相关系数大于近区,且更接近1,无论在近区还是远区,垂向分量的相关系数均为最大。
(2) 近区当比例距离小于5时,径向振速最大,比例距离大于等于5时,垂向振速最大。远区垂向振速最大。无论在近区还是远区,切向振速一般最小。
(3) 振速三分量在近区的变异系数均大于远区,径向振速的变异系数在近区和远区较为接近。
(4) 最大段药量或爆心距增加时,从能量比例上看,近区及远区的能量都会向低频带流动,近区的移动速度要快于远区;同时近区及远区能量分布的频带宽度也将趋于集中,近区的频带宽度也要大于远区。
[1] 李保珍. 露天深孔爆破地震效应的研究[J]. 长沙矿山研究院季刊, 1989,9(4):84-94.
LI Baozhen. Vibration effect of longhole blasting in open pit mining[J]. Quarterly of CIMR, 1989,9(4):84-94.
[2] 张在晨,林从谋,黄志波,等. 隧道爆破近区振动的预测方法[J]. 爆炸与冲击, 2014, 34(3): 367-372.
ZHANG Zaichen, LIN Congmou, HUANG Zhibo, et al. Prediction of blasting vibration of area near tunnel blasting source[J]. Explosion and Shock Waves, 2014, 34(3): 367-372.
[3] 杨年华. 爆破振动理论与测控技术[M]. 北京: 中国铁道出版社, 2014:48.
[4] 韩亮. 深孔台阶爆破近区振动效应的试验研究[D]. 北京: 中国矿业大学(北京), 2016: 19-25.
[5] 杨年华,张志毅,王平亮,等. 大规模深孔抛掷爆破振动衰减实测与研究[M]. 北京: 冶金工业出版社, 2008: 721-726.
[6] 中国生,敖丽萍,赵奎,等. 基于小波包能量谱爆炸参量对爆破振动信号能量分布的影响[J]. 爆炸与冲击, 2009, 29(3): 300-305.
ZHONG Guosheng, AO Liping, ZHAO Kui, et al. Influence of explosion parameters on energy distribution of blasting vibration signal based on wavelet packet energy spectrum[J]. Explosion and Shock Waves, 2009, 29(3): 300-305.
[7] 凌同华,李夕兵. 最大段药量对爆破振动信号频带能量分布的影响[J].采矿技术, 2003, 3(4):21-24.
LING Tonghua, LI Xibing. Influence of maximum explosive blasted per delay on frequency bands energy distribution of blasting vibration signals[J]. Mining Technology, 2003, 3(4):21-24.
[8] 卢文波,王进攻. 爆源中远区的爆破振动场模拟[J].爆破,1996,13(3):8-11.
LU Wenbo, WANG Jingong. A simulation of blasting vibration in middle and far field of explosion source[J]. Blasting, 1996, 13(3): 8-11.
[9] 杨年华,张乐. 爆破振动波叠加数值预测方法[J]. 爆炸与冲击, 2012, 32(1): 84-90.
YANG Nianhua, ZHANG Le. Blasting vibration waveform prediction method based on superposition principle[J]. Explosion and Shock Waves, 2012, 32(1): 84-90.
[10] 徐全军,毛志远,张庆明,等. 深孔微差爆破震动预报浅析[J].爆炸与冲击, 1998, 18(2): 182-186.
XU Quanjun, MAO Zhiyuan, ZHANG Qingming, et al. The analysis of ground vibration prediction of delay-fired bench blasting[J]. Explosion and Shock Waves, 1998, 18(2): 182-186.
Experimental study on vibration characteristics of deep hole bench blasting in both near and far field
HAN Liang1,XIN Chongwei2,LIANG Shufeng3,LIU Dianshu3
(1. Safety Engineering College, North China Institute of Science and Technology, Beijing 101601, China;2. School of Civil and Resources Engineering, University of Science and Technology Beijing 100083, China;3. School of Mechanics & Civil Engineering, China University of Mining and Technology (Beijing), Beijing 100083, China)
In order to explore the vibration characteristics of deep hole blasting in near and far field, based on field test, this paper used the regression analysis, random analysis and wavelet packet decomposition to carry on a comparative study from the attenuation, three-component characteristic, random characteristic and energy distribution of blasting vibration signals. The results show that the values ofKandαof the three-component of vibration velocity in the near field are both greater than those in the far field. The value ofαof each component in the far field is closer to each other. The correlation coefficient of the three-component vibration velocity in the far field is greater than that in the near field, and closer to 1. The vertical component in the three components is the largest. In the near field, when the scaled distance is less than 5, the radial velocity is the largest, otherwise, the vertical velocity is the largest. In the far field, the vertical velocity is always the largest. Both in the near and far field, the tangential velocity is generally minimal. The coefficient of variation of the three components of vibration velocity in the near field is larger than that in the far field, and the coefficient of variation of the radial velocity are close in the near and far field. When the maximum charge weight per delayed interval or distance is increased, energy in the near and far field gradually move toward the low frequency band, in which it moved faster in near field. At the same time, the frequency band width of energy distribution in the near and far field also tend to focus, and the frequency band width in near field is larger.
deep hole blasting; near field; regression analysis; attenuation law; random variables; energy distribution; wavelet packet
2016-11-10 修改稿收到日期:2016-12-19
韩亮 男,博士,1985年生
刘殿书 男,教授,博士生导师,1960年生
E-mail: lds@cumtb.edu.cn
TD235
A
10.13465/j.cnki.jvs.2017.08.011
