利用多媒体教育平台激活学生数学思维探究
2017-04-17蔡春民
蔡春民
[摘 要] 多媒体教育平台已经相对普及,发掘其功能是学科教学的关键.高中数学教学中,基于思维激活的思路去使用多媒体教育平台,从数学直观、思维拓展、知识体系构建等角度实现数学教育与多媒体教育平台的结合,是科学有效的教学思路. 实际教学中,教师要将两者的结合进一步与具体的知识构建或教学环节联系起来,同时注重问题解决教学中多媒体教育平台的使用.
[关键词] 高中数学;多媒体教育平台;数学思维
作为现代教学手段的使用,多媒体教育平台已经成为不少地区教室的标配,笔者所在的地区,集计算机、液晶投影仪、实物投影仪、多点触控显示器、音响等于一体的多媒体教育平台,在高中学校已经基本普及,而对其作用的充分发掘,也成为教师关注的一个重点. 从已有研究来看,基于多媒体教育平台自身的功能去发掘其教育功能,是常规的思路,但这种思路难免导致课堂上的一些华而不实的现象的发生,因此在笔者看来,更多的还是要从学科特点出发,让多媒体教育平台更多的服务于学科教学,而不是牵着学科教学的鼻子走.
一旦将研究的重点放到学科教学上,那教师要关注的就是学科自身的特点以及对多媒体教育平台的作用判断了.高中数学教学中,最重要的就是學生思维的拓展,只要学生的数学思维得到了充分的激活,那学生的数学学习就会处于一个快车道之上,而在传统的教学手段作用下,由于高中数学知识的抽象性,学生的思维往往缺少一个形象基础,或者缺少一个科学的逻辑过程,有了多媒体教育平台的辅助,这些困难有可能被克服,学生的数学思维就有可能被激活,从而真正实现让多媒体教育平台服务于高中数学学科的教学,从而也就体现了多媒体教育平台的“辅助”作用.
[?] 数学直观,多媒体教育平台的基本功能
高中数学难学的一个重要原因,在于数学知识的抽象性,而所谓的抽象,就是学生在用自身的思维加工数学知识的时候,缺少一个基本的形象支撑,以至于学生的形象思维难以发挥作用,因此只能通过抽象思维来加工数学知识.但稍有教育心理学知识的教师都知道,没有必要的形象思维,抽象思维是难以充分发挥作用的. 高中数学知识中,从最基本的集合知识,到多种函数组成的函数体系,从抽象的符号语言到图形语言,其实都是需要形象思维的,只有形象思维的作用得到了充分发挥,学生的抽象思维及建立在其基础上的直观思维,才有可能成为引导学生学习新的数学知识、解决新的数学问题的动力. 从另一方面来看,数学直观也是学生数学素养的重要组成部分,因为在数学素养的六个组成部分中,直观想象就是一个重要的维度,而直观想象素养的形成过程中,多媒体教育平台是可以发挥重要的作用的.
多媒体教育平台最基本的功能说得通俗一点,就是声光电的作用,声音信息可以刺激学生的听觉,光电信息可以刺激学生的视觉,而这两个通道一旦被有效打通,学生构建数学知识的过程就可以变得十分的顺利. 以“函数的单调性”教学为例,笔者在教学过程中有意识地结合不同的函数的图像特征,在阶段性复习的过程中,借助于多媒体教育平台以及几何画板等应用软件的使用,让学生观察不同的函数的图像在相应的定义域内的单调性. 这是一个给学生呈现动态画面的过程,如果从细节处来描述则是:从学生最熟悉的一次函数开始,到二次函数,到三角函数,再到指数函数与对数函数,每一个函数都有其对应的定义域,在相应的定义域之内,函数的图像也都会呈现出不同的单调性,而且这种单调性在多媒体教育平台上,是以动态的形式出现的,在动态呈现函数的单调性的过程中,学生的思维常常会基于自身的思考而做出预测,当屏幕上所呈现的单调性符合学生的预期的时候,就起到了知识巩固的作用. 而如果出乎学生的意料,则又可以给学生以一种打破原有认知平衡并建立新的认知平衡的作用. 无论是哪种作用的发挥,背后都是形象思维在起着支撑作用,而随后学生的抽象思维就可以促进自身知识的构建,从而形成良好的数学直觉.
根据教学经验,我们可以这样认定多媒体教育平台的基本功能就是帮助学生形成良好的数学直观,而这也是学生数学学习的第一扇大门,如果在多媒体教育平台的辅助之下,学生能够顺利地进入这扇大门,那数学的有效学习就迈开了坚实的第一步.
[?] 思路拓展,多媒体教育平台的核心功能
从学生的数学思维角度来研究多媒体教育平台的作用可以发现,学生在数学学习中的另一个难点即思维困境的突破,是数学学习质变的重要环节. 很多时候,我们说学生的数学学习不理想,就是因为在数学思维的关键点难以形成有效的突破,而这种现状如果得不到有效改变,就会让学生的数学思维长期处于这种低水平的思维状态,这自然是无法有效学习数学的. 而进一步的研究表明,多媒体教育平台恰恰可以在这个方面发挥重要的作用. 这里以数学问题的解决为例,来阐述这一思路.
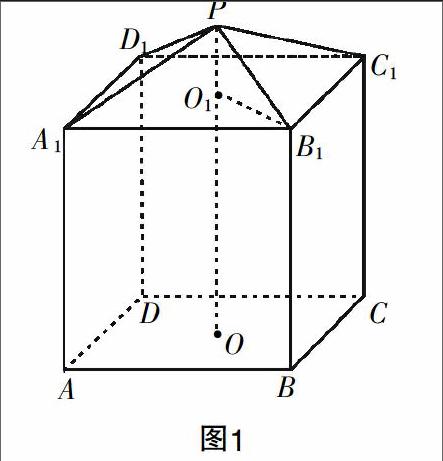
高中数学教学中,问题解决是最核心的一个环节,数学知识的运用基本上全部体现在数学问题解决的过程中. 数学问题解决,就是学生利用数学学习过程中形成的数学思维,去利用数学知识形成解题思路的过程. 问题解决过程中,思维是一个关键,而思维难点的突破则是关键中的关键.这是2016年江苏高考卷的第十七题:现需要设计一个仓库,它由上下两部分组成,上部分的形状是正四棱锥P-A1B1C1D1,下部分的形状是正四棱柱ABCD-A1B1C1D1(如图1所示),并要求正四棱柱的高OO是正四棱锥的高PO1的4倍. (1)若AB=6m,PO1=2m,则仓库的容积是多少?(2)若正四棱锥的侧棱长为6m,则当PO1为多少时,仓库的容积最大?
图1
在本问题解决的过程中,需要让学生认识到几何体的体积是两个体即柱体与锥体之和,此时可以借助于多媒体教育平台,让这个几何体分成柱体与锥体两个组成部分,从而给学生形成一种良好的数学直观.更重要的是,在问题解决的过程中,应当引导学生去进一步分析,以让学生发现PO1是本题中建立体积函数关系式的一个关键的自变量,而这也是本题的一个思维难点. 怎样让学生顺利地想到这一点呢?笔者在教学中借助于应用软件,在对下面的柱体与上面的锥体进行分离组合的过程中,让学生认识到只有PO1这个变量才是联系上下两个几何体的唯一变量,因此以之为自变量,才可以建立起关于上下锥体与柱体体积的关于同一个变量的函数关系式.考虑到所教学生的实际基础,笔者发现如果不借助于多媒体教育平台,那只可能在原来的图上进行思维加工,而原图是“死”的,如果学生的空间思维能力不够,那学生的思维也就有可能“死”在这一个环节上.而有了多媒体教育平台,学生的思维就活了起来,他们就会对原来的两个体有一种直观的认识,从而对联系两体的变量产生直觉性的理解. 这种直觉恰恰是拓展思维的关键,是解题思路打开的关键,一旦此点形成有效的突破,整个解题过程也就敞亮了起来.
在高中数学教学中,借助于多媒体教育平台,在问题解决(当然也包括其他的数学知识建构)过程中形成有效的思路突破,就可以帮学生形成良好的数学思维品质.
[?] 知识体系,多媒体教育平台的附加功能
在多年的高中数学教学中笔者还发现,数学能力最终形成的一个标志,就是学生对数学知识体系的构建. 很多时候,笔者发现即使到了高三阶段,学生的数学知识体系仍然不够完善,他们在提取运用数学知识的时候,还感觉存在困难. 而这个时候已经进入复习阶段,如果采用传统的知识结构图或者知识树的方式,那不仅费时费力,且效果也不太明显. 于是教学不可避免地进入了题海状态. 笔者在教学中从学生的思维特点出发,尝试借助于多媒体教育平台,让学生在复习的过程中形成一个动态的知识结构图,取得了较好的效果.具体的做法就是:在知识体系的复习过程中,借助于多媒体教育平台,先呈现一个核心概念(如“函数”),然后围绕这个核心概念,让学生去思考有哪些相关的概念,并在屏幕上进行即时的展示(可以将课件设计成交互功能),学生想到哪个概念,就呈现哪个概念,同时借助于线段或箭头以表示知识之间的从属关系.
这样的一个知识体系建构过程最大的优点就是动态的,而这个动态又是以学生的思维为基础的. 因此最终呈现出的知识结构图,实际上也就是学生的一个思维导图,反映的是学生的思维现状,暴露的是学生某个知识联结点的不足,而在合作学习中,这种不足又可以得到即时的修正. 这样,一个面向全体学生的知识体系建构过程就出现在学生的面前.
事实证明,这一功能对学生构建数学知识体系是非常有效的,如果说其稍有难度的话,那就是交互功能的实现,这里有两个方法:一是PPT上的即时输入,另一个是借助于一些多媒体制作软件去进行. 前者易而后者难,各人根据自己的实际水平选择即可.
