水波变化演示与三角函数的特征分析

北京101中学 方雯琪

水波变化演示与三角函数的特征分析

北京101中学 方雯琪

在学习高中数学当中，三角函数占有较大的比例，并且三角函数的部分内容也是高考主要考查的内容，因此，在我们学习三角函数的过程中必须要注重学习方法。而在数学学习的过程当中，数形结合的思想是重要的学习指导思想之一。如果要深入理解三角函数，深刻掌握三角函数的内容，可以尝试以水波变化演示的方法进行学习。本文主要以三角函数的相关例题为切入点，使用水波变化演示的方法，体现数形结合的思想，并展现三角函数的特征。

水波变化演示；三角函数；特征

在我们学习三角函数的过程当中，很多情况下借助图象可以更好地了解三角函数，通过图象我们可以了解掌握三角函数的图象如何呈现、三角函数的性质、三角恒等变换和解三角形问题等相关的知识。因此，本文当中所提及的水波变化演示函数的学习方法，主要是通过水波图象的形式呈现三角函数的相关内容。根据三角函数的图象看，其形状与水波相似，因此本文以下的内容是从三角函数的例题入手，在水波变化演示下分析三角函数的特征。

一、水波演示呈现正弦函数y=sinx的图象与性质

在我们的头脑中，水波变化大致呈现的是一种波浪形的画面，而正弦函数y=sinx的图象实际上与水波相似，如图所示：

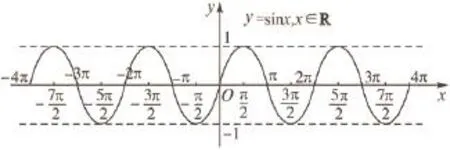
从该图象中，我们可以看出正弦函数y=sinx的定义域为R，值域为[-1，1]，属于奇函数，其单调增区间是，单调减区间为。依据水波变化演示图象，可以很清楚地看出正弦函数相关的定义域、值域等，对正弦函数的性质了解就更为清楚。为扩展我们对图象的理解能力以及进一步呈现水波变化演示，掌握正弦函数图象的画图规律，可以在正弦函数y=sinx的基础上进行扩展，例如将其扩展为y=2sinx或，先尝试着画出图象，如下图所示：

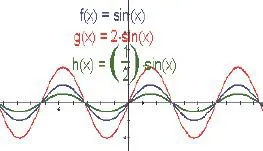
依据图象以及水波变化演示看，正弦函数在一定的范围之内呈周期性波动，并且对其值域以及单调增区间和单调减区间也一目了然。实际上，水波变化演示与三角函数图象是极为相似的，通过一定的周期呈现出波纹的形状。图中的曲线y=2sinx和是在曲线y=sinx的基础上进行了不同的伸缩，体现出的值域有所不同，但这三种形式的周期以及定义域并没有变化。