浅析错位相减在数列中的应用

中国人民大学附属中学分校 徐 可

浅析错位相减在数列中的应用

中国人民大学附属中学分校 徐 可

在高中数学知识体系中，数列知识占据很重要的位置，而数列知识中数列的求和又是重点内容，尤其是“错位相减”这种重要方法的运用。在学习数列知识的过程中，我们通常仅仅关注了掌握和运用求和公式，却忽视了在推导求和公式的过程中涉及的“错位相减”这种重要的方法，导致在解答此类数列求和的问题时无能为力。此外，在每年的数学高考卷中，很多省的试题中都考查了用错位相减法处理数列求和问题，其重要性毋庸置疑。基于此，本文将首先说明错位相减这种方法，然后举例其在数列求和中的应用。

错位相减；数列；求和

一、错位相减方法说明

通常，我们习惯性地称求解等比数列前n项和Sn的方法为“错位相减法”。实际上，高中教材里出现的求和问题仅仅是某一类数列求和问题中的特例，下面我们将其推广为更加普适的求和问题，即“一个非零等差数列与一个等比数列的对应项之积构成的新数列的求和”。

【定理】现已知数列｛an｝、｛bn｝分别表示等差和等比数列，数列的首项分别是a、b，等差数列的公差是d，等比数列的公比是q（q≠1）。新数列cn=an·bn，那么该数列的前n项和。

【评析】通过观察以上证明过程，我们可以看到，所谓“错位”是为了“对位”，即将公比的幂方相同的项一一对齐；而对好位是方便整体“并项”，并完项才能通过等比数列求和公式进行求和。

此外，需要注意的是，以上错位相减中我们采用的是在求和式子的两边都乘等比数列的公比，即两边均乘q。然而错位相减在数列中的运用不仅仅是这一种形式，同学们需要多见识题型，熟悉掌握每一种形式，并注意归纳总结。下面举例说明另一种“错位相减”的形式：在已知数列前n项和公式Sn=f（n）的情况下，求解通项公式an。这类题的解题步骤如下：（1）错项，所谓“错项”，是指在Sn=f（n）的基础上写出Sn-1=f（n-1）；（2）相减，将（1）所得关系式同原关系式对应相减，即：；（3）求通项，根据Sn- Sn-1=an可以得到：。这种形式的“错位相减”最后需要验证a1是不是满足an=f（n）-f（n-1）（n≥2），若满足，那么通项就能简化为an=f（n）-f（n-1）（n=1，2，3，…）。同时，此种形式下的“错位相减”能够广泛运用到有关Sn同an的混合关系式以及an与an+1的复杂递推关系式当中，能够逐步将数列问题的类型进行转换。

了解了“错位相减”是怎么回事之后，接下来本文将举例说明几种常见的其在数列中的运用。这并不是全部，但希望给同学们启发，以后自己遇到类似题目不会做的时候，能够记得试一试“错位相减”。

二、错位相减在数列中的运用举例

1．实现混合关系式Sn=f（an）转化为递推公式an+1=f（an）

这类题指的是题目中出现表示Sn和an关系的式子，这时候我们可以利用“错位相减”，首先将Sn和an均退一项，得到Sn-1和an-1的关系式，再将两个关系式进行对应相减。

例1 已知数列｛an｝满足：an＞0，并且有，试证明：数列｛an｝为等差数列。

【评析】在本题中正是利用错位相减这种方法，将混合关系式Sn=f（an），即化成通项之间的递推式：-an=4，从而得知数列是以4为公差的等差数列。

2．实现复杂的通项关系转换

当我们在做题中碰到比较复杂的通项关系时常常不知所措，其实我们只要在结合具体题型特点的情况下，充分发挥“错位相减”这种方法，将问题的类型实施转换就可以轻松解决。下面先看个简单例题感受一下，再举例一道高考题。

例2 已知数列｛an｝满足以下条件：，试证明：数列｛an｝为等差数列。

【答案】证明：由已知条件可以知道：

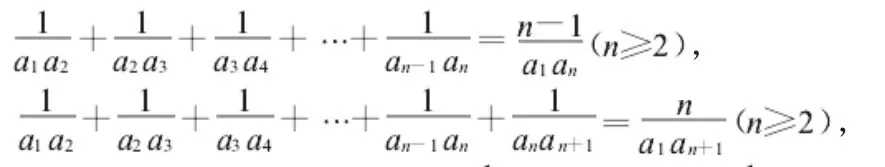
也就是：。（备注：这里为第一次使用“错位相减法”）

【评析】在本题中运用了两次“错位相减”。首次的“错位相减”是为了把复杂的通项进行简化，显然经过一次“错位相减”后得到的仍是较为复杂的两连项的递推关系：nan=a1+（n-1）an-1；于是我们进行第二次“错位相减”，这样就得到等差数列的递推式（不完整的）。尽管此题中结果有点“巧合”，但就算不是如此“幸运”，我们对接下来如何去想也早已心知肚明。

例3 （2009年全国卷I）在数列｛an｝中，a1=1，，试求：

（2）求数列｛an｝的前n项和Sn。

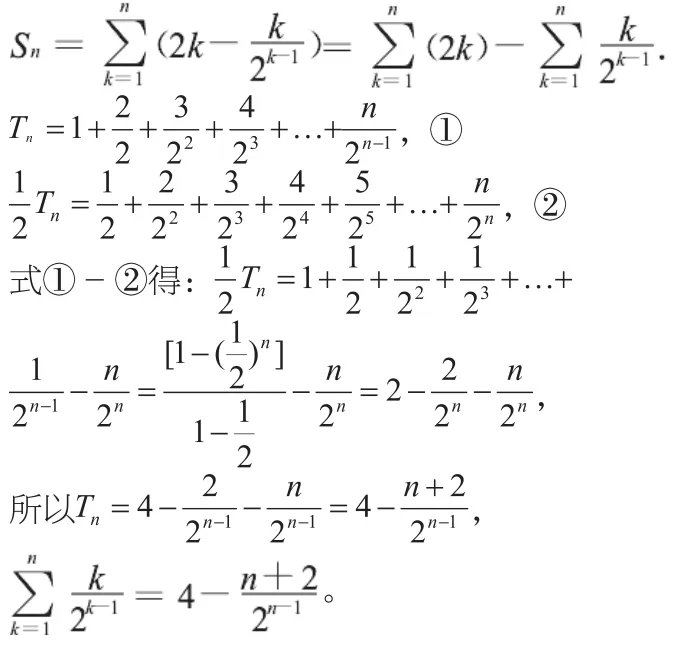
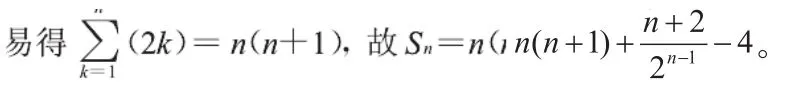
【评析】在这道2009年全国I卷的考题中，考查的是利用构造新数列和“错位相减法”求解数列前n项和。在以往的考题中，压轴题通常是以数列结合不等式考查放缩法问题，引导考生和一线教师重视数学教材和基础知识、基本方法以及基本技能，并重视教材中所涉及的重要方法的运用。然而这道题目可以看到出题老师有着降低难度以及力求变化的决心，这道题中解题关键在于熟练掌握解决数列问题的一些常见的但却很重要的方法，例如迭加法、错位相减法等等，所以同学们应该重视起“错位相减法”的运用。

3．实现Sn与an的高次关系的转换

有时候题目中的已知条件是Sn和an之间的高次关系式，同学们面对这种问题也不要不知所措，其实对于任何高次问题，基本原则便是“降次”，只是视具体情况不同而有不同的降次方法。在数列中，遇到Sn和an这种高次关系，我们通常是使用“错位相减法”进行降次。可能“错位相减”需要用到多次，但是无论怎样，我们的目的就是将高次不断降低，直到明晰化递推关系。

例4 现有一数列｛an｝，其前n项和Sn满足：n属于任意正自然数），试求数列的通项公式。

综上所述，an+1-an=1(n∈N＊），故数列｛an｝是以1为首项，1为公差的等差数列，即an=n。

【评析】可以看到，本题中也使用了两次错位相减，目的就是不断“降次”。这不禁让我们再一次感受到“错位相减法”的精妙。

综上所述，所谓“错位相减”便是将已知关系式进行“错项再联合”，这种方法不仅仅展现出其充分挖掘已知条件的魅力，又体现出其整体运算的巧妙所在。“错位相减”有时候不止用一次，它可能使用两次或多次，视具体题目而定，这一次或多次“错位相减法”的运用便将问题由复杂转换成简单，由开始做题时的“一团乱麻”变成答案“唾手可得”。因此“错位相减”是解决数列求和问题非常实用的一种方法，希望同学们细细体会，掌握这种方法的精髓，争取在数列求和问题中“战无不胜”。

[1]李晓燕．数列中错位相减求和法之应用举例[J]．神州旬刊，2013（14）：191-191．

[2]陈胜华．数列错位相减法求和新探[J]．新课程学习·中旬，2013（5）．

[3]谭杭军．关于数列中错位相减法的进一步思考[J]．数学学习与研究，2015（7）：129-130．