带有p-Laplacian算子的分数阶四点边值问题正解的存在性

刘 洋, 李 东

(1.合肥师范学院 数学与统计学院, 安徽 合肥 230601; 2.佳木斯大学理学院 数学系, 黑龙江 佳木斯 154007)

带有p-Laplacian算子的分数阶四点边值问题正解的存在性

刘 洋1, 李 东2

(1.合肥师范学院 数学与统计学院, 安徽 合肥 230601; 2.佳木斯大学理学院 数学系, 黑龙江 佳木斯 154007)

利用不动点定理,研究了带有p-Laplacian算子的分数阶微分方程四点边值问题正解的存在性,得到该边值问题至少存在一个正解的充分条件.

不动点定理; 正解;p-Laplacian算子

0 引言

近年来, 分数阶微分方程和带p-Laplacian算子的微分方程受到了众多数学学者的广泛关注, 并取得了许多有意义的研究成果[1-5]. Han等利用不动点定理[1], 得到了如下带有p-Laplacian算子的分数阶微分方程边值问题正解的存在性

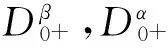
(1)

(2)

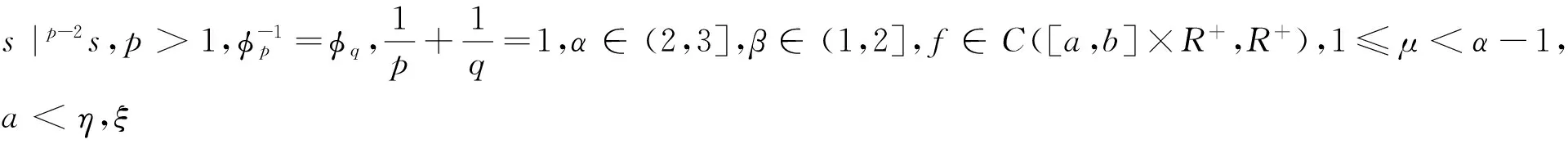
1 预备知识和引理

引理1 假设y∈C[a,b], 则分数阶边值问题

(3)

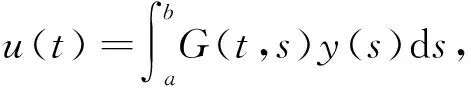
证明 易知问题(3)的唯一解等价于

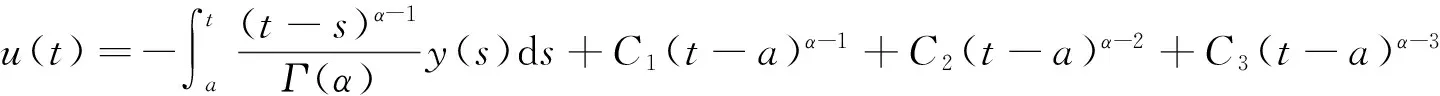
由式(3)的边值条件知,

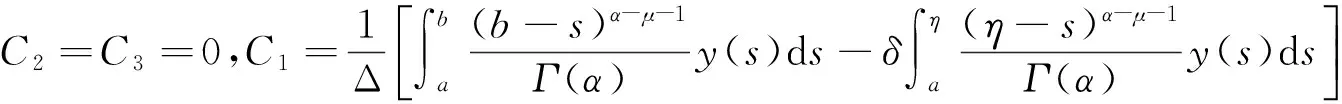
故

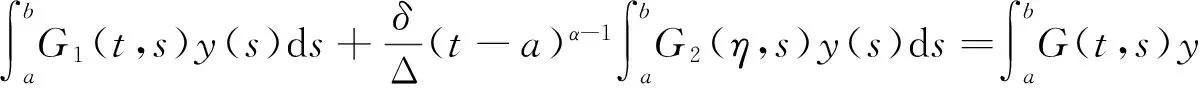
引理2 假设w∈C[a,b], 则分数阶边值问题

(4)

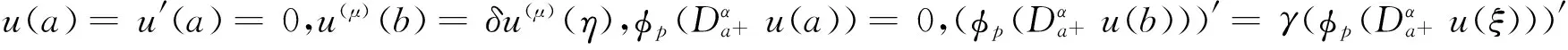
(5)

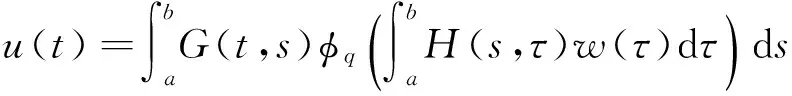
证明 易知问题(4)等价于

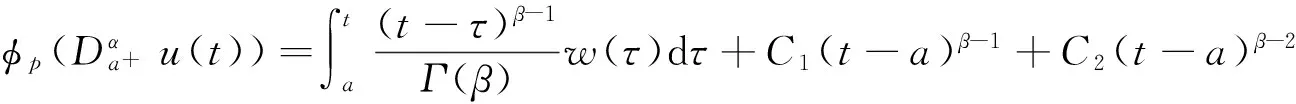
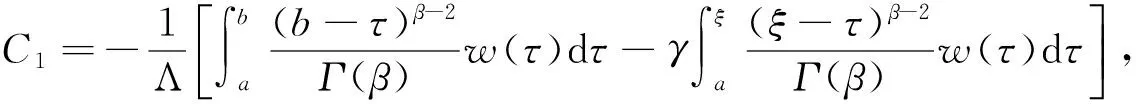
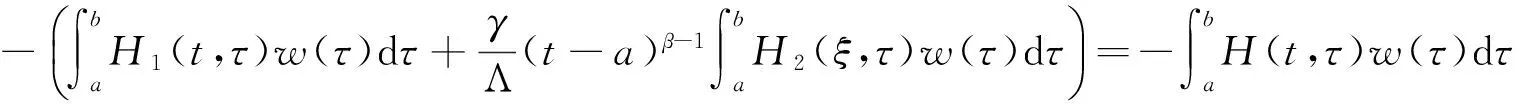
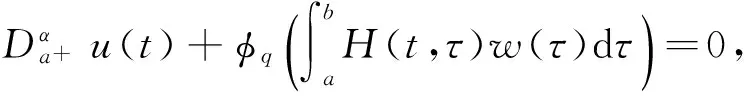
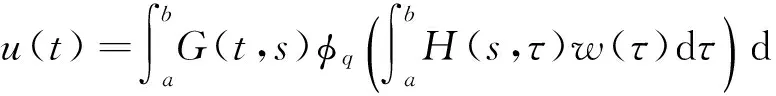
引理3G(t,s)有如下的性质:

(i) 当(t,s)∈[a,b]×[a,b]时, 0≤G(t,s)≤G(b,s);

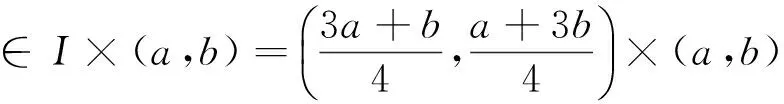
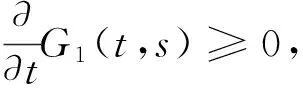
当t≥s时,

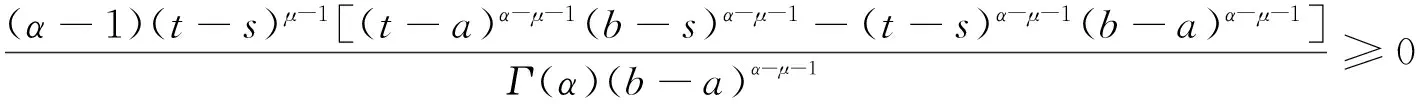
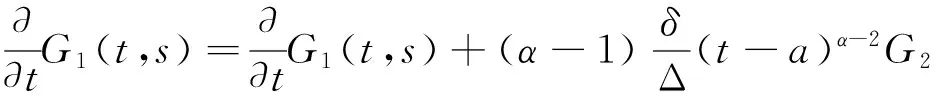
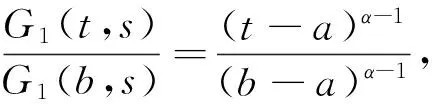
当t≥s时,

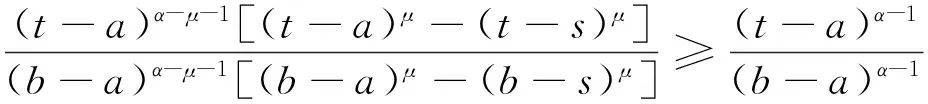
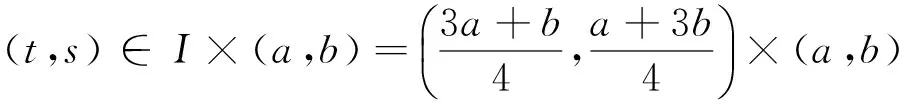
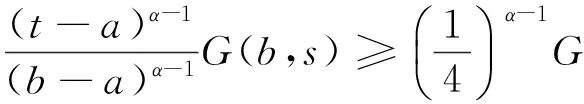
引理4H(t,s)有如下的性质:

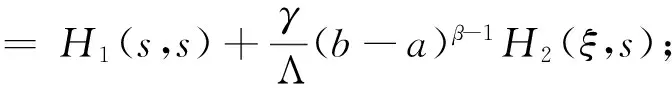
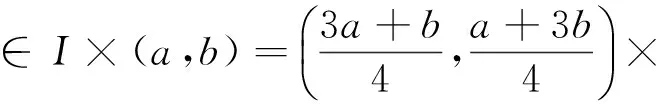
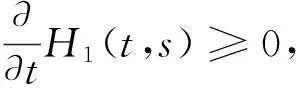
当t≥s时,

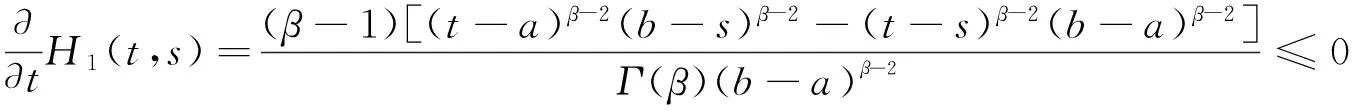
故 0=H1(a,s)≤H1(t,s)≤H1(s,s), 因此, 当(t,s)∈[a,b]×[a,b]时,

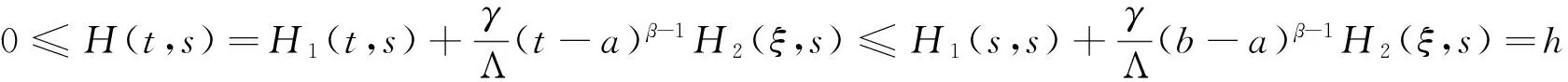
即(i) 成立.

则

g(s)H1(s,s).

2 主要结果

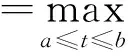
定义算子T:E→E, 对任意的u∈E, 有

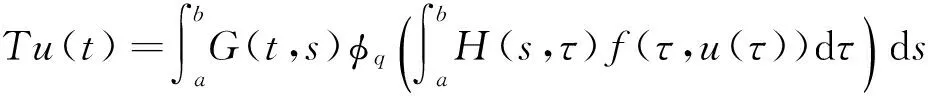
为了方便,引入以下记号:

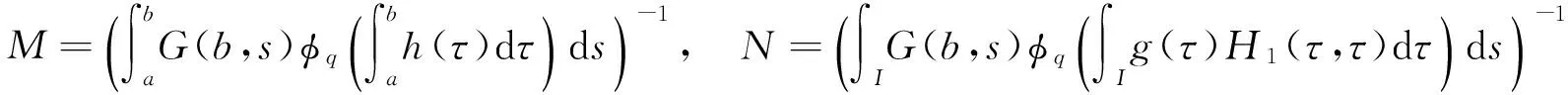
定理1 若存在两个正数λ1,λ2使得λ1<λ2, 且

(B1)当(t,u)∈[a,b]×[0,λ1]时,f(t,u)≥φp(λ1N4α-1);

(B2)当(t,u)∈[a,b]×[0,λ2]时,f(t,u)≤φp(λ2M),

则分数阶四点边值问题(1)和(2)至少存在一个正解u, 并且满足λ1≤‖u‖≤λ2.

证明 首先我们证明算子T:K→K是全连续的, 事实上由G,H,f的连续性可知T:K→K是连续的.对于(t,s)∈I×(a,b),u∈K,由引理3,我们有

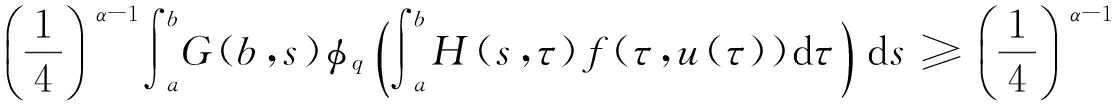
这意味着T(K)⊂K. 故应用Arzela-Ascoli定理易证算子T:K→K是全连续的.

下面我们令Ω1={u∈K:‖u‖≤λ1},那么对于u∈∂Ω1,由引理3,引理4及(B1)知

故当u∈∂Ω1时, ‖Tu‖≥‖u‖.

令Ω2={u∈K:‖u‖≤λ2},那么对于u∈∂Ω2,由引理3,引理4及(B2)知

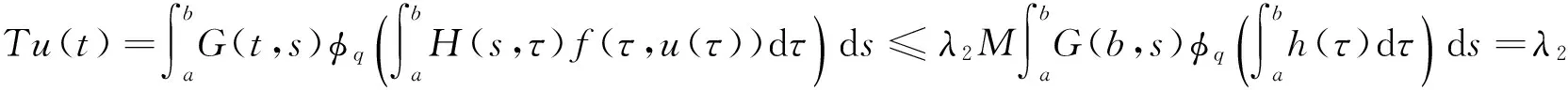
于是,当u∈∂Ω2时,‖Tu‖≤‖u‖.

综上,由不动点定理[1]知,分数阶四点边值问题(1)和(2)至少存在一个正解u, 并且满足λ1≤‖u‖≤λ2.

[1] Han Z,Lu H,Zhang C. Positive solutions for eigenvalue problems of fractional differential equation with generalized p-Laplacian[J]. Appl Math Comput,2015,257(1):526-536.

[2] Wu Y,Li X,Jiang W. Some results for two kinds of fractional equations with boundary value problems[J]. J Math, 2016,36(5):889-897.

[3] 王和香,胡卫敏. 一类具p-Laplacian算子的含积分边界条件的分数阶微分方程边值问题解的存在性[J].数学的实践与认识,2016,46(16):228-236.

[4] 王勇.非线性分数阶微分方程积分边值问题的正解[J].应用数学,2016,29(1):1-6.

[5] 袁幼成,周辉,周宗福. 一类分数阶微分方程多点共振边值问题解的存在性[J].合肥师范学院学报,2016,34(3):5-9.

[责任编辑：李春红]

Existence of Positive Solutions for a Fractional Four-point Boundary Value Problem withp-Laplacian Operator

LIU Yang1， LI Dong2

(1.School of Mathematics and Statistics, Hefei Normal University, Hefei Anhui 230061, China) (2.Department of Mathematics, College of Science Jiamusi University, Jiamusi Heilongjiang 154007, China)

In this paper, by using the the fixed point theorem, we obtain the existence of the positive solutions for a fractional four-point boundary value problem withp-Laplacian operator.

fixed point theorem; positive solution;p-Laplacian operator

2016-12-03

安徽省自然科学基金重点资助项目(KJ2014A200); 黑龙江省教育厅科学技术研究资助项目(12543079)

刘洋(1983-), 女, 吉林长春人, 讲师, 硕士, 研究方向为非线性泛函分析. E-mail: yangl@hfnu.edu.cn

O175.8

A

1671-6876(2017)01-0001-05