MATLAB 软件在线性代数教学中的应用

刘 蒙

(淮阴师范学院 数学科学学院, 江苏 淮安 223300)

MATLAB 软件在线性代数教学中的应用

刘 蒙

(淮阴师范学院 数学科学学院, 江苏 淮安 223300)

结合Matlab的特点和线性代数课程教学的现状,以线性代数教学中的一些知识点为例,说明了Matlab在线性教学中的一些应用,以期可以激发学生学习的积极性,提高教学效率．

Matlab; 线性代数; 教学

0 引言

线性代数是高等院校计算机、物理、电子信息等理工类专业以及经济管理、市场营销、财务管理等财经类专业必修的一门重要的数学类公共基础课,是学生学习诸多后续课程的重要理论基础,对培养学生的思维能力非常重要．该课程的理论不仅渗透到了数学的许多分支中,而且在物理、化学、生物、工程技术、经济、金融、技术等领域中都有着广泛的应用,日益成为学生在以后的工作中解决工程应用问题的重要理论工具．但是线性代数课程本身含有大量比较抽象、较难理解的内容,且在很多高校该课程课时量偏少,长期以来学生普遍感到该课程难以学习,一学期结束不知所学何物．因此,如何通过改革教学方法和手段提高线性代数的教学效果和学习质量成为了学者们普遍关心的问题．

随着计算机软件技术的快速发展,将数学软件引入到线性代数的教学中已经成为该门课程教学改革的研究热点．在众多数学软件中,Matlab应用最为广泛．该软件是1984年由美国MathWorks公司研制开发,和Mathematica、Maple并称为三大数学软件,其在数值计算方面首屈一指[1]．将Matlab软件恰当地引入到线性代数的教学中不仅可以降低教与学的难度、激发学生的学习兴趣,还可以提高学生的理解能力[2-4]．本文通过几个例子对Matlab软件在线性代数教学中的应用进行了初步探讨,同时给出了若干建议．

1 Matlab在行列式教学中的应用

线性代数课程的第一章通常是行列式[5]．行列式是一个非常基本和重要的概念,17世纪由日本数学家关孝和提出,其后由莱布尼茨、克莱姆、贝祖、范德蒙德、拉普拉斯、拉格朗日、凯莱、柯西、雅克比等著名数学家发展形成了系统的理论,在多个领域有着重要的应用．求行列式值的方法多种多样,例如:定义法、 按行(列)展开法、数学归纳法、递推法、乘法法则、升阶法、拆项法等．教师除了可以向学生介绍以上计算行列式的方法, 还可以利用Matlab软件计算并向学生展示其便利性．这样学生在日后的工作中若需要计算较复杂的行列式可以借助Matlab 软件,克服难题．

在Matlab中计算行列式的语言命令格式为: det(A), 其中A若是符号矩阵,则返回结果是符号表达式;若A是一个数值矩阵,则返回结果是一个数值．

例1[5]计算四阶行列式

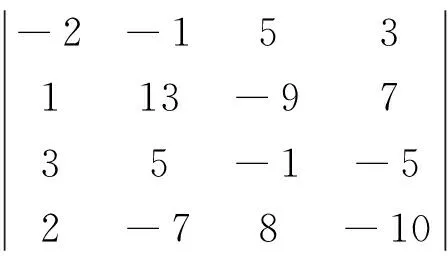
在Matlab窗口中输入:

≫A=[-2-1 5 3; 1 13-9 7; 3 5-1-5; 2-7 8-10]; %定义数值矩阵

≫D=det(A) %求矩阵A的值

执行命令,即可得到所求值为:D=-312.

例2 计算三阶行列式

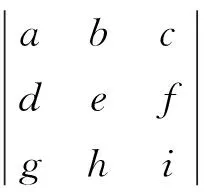
在Matlab 窗口中输入:

≫ symsabcdefgh%定义系统符号

≫A=[abc;def;ghi]; 定义符号矩阵

≫D=det(A) %求行列式的值

执行命令,即可得到所求值为:

D=i*a*e-a*f*h-i*d*b+d*c*h+g*b*f-g*c*e.

2 Matlab在矩阵教学中的应用

矩阵是线性代数课程中最重要的概念,其各种运算有各自具体的计算方法,但是都比较繁琐,而使用Matlab计算仅需一个简单命令即可实现,因此在矩阵的教学中恰当引入Matlab可以有效地激发学生的学习兴趣,提高学习效率．

2.1 矩阵的加/减法

在Matlab中进行矩阵加/减法运算要求相加/减的两个矩阵具有相同的行数和列数,否则不能相加/减．

例3[5]设

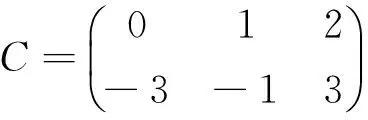
求3A-2B+C.

在Matlab窗口中输入:

≫A=[2 4 1; 0 3 5];B=[-1 3 1; 2 0 5];C=[0 1 2;-3-1 3]; %定义数值矩阵

≫ 3*A-2*B+C

执行命令,即可得到所求结果为

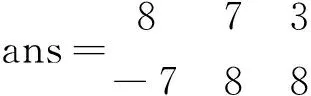
即:

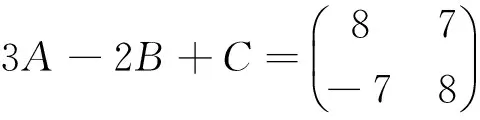
2.2 矩阵的乘法

在Matlab 中进行矩阵乘法运算要求左边矩阵的列数与右边矩阵的行数相同,否则不能相乘．值得注意的是,矩阵的乘法一般不满足交换律(AB≠BA)和消去律(AB=AC且A是非零矩阵推不出B=C)．

在Matlab 窗口中输入:

≫A=[1 0-1 2;-1 1 3 0; 0 5-1 4];B=[0 3 4; 1 2 1; 3 1-1;-1 2 1]; %定义数值矩阵

≫A*B,B*A

执行命令,即可得到所求结果为

即:

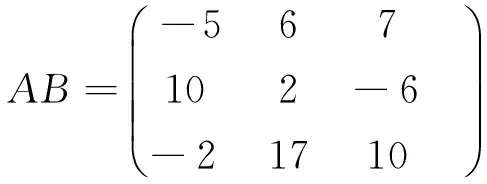
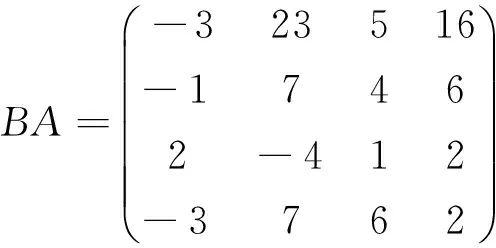
这个例子也说明了矩阵的乘法一般不满足交换律．

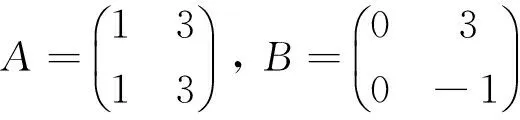
在Matlab窗口中输入:

≫A=[1 3; 1 3];B=[0 3; 0-1];C=[6 0;-2 0]; %定义数值矩阵

≫A*B,A*C

执行命令,即可得到所求结果为

即:

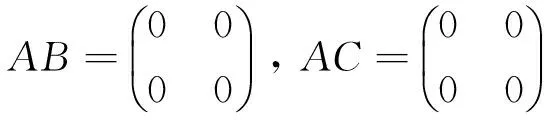
这个例子在说明了矩阵的乘法一般不满足消去律的同时还说明了非零矩阵的乘积可以是一个零矩阵．

2.3 矩阵的转置

矩阵A的转置是指将该矩阵的行变成列、列变成行形成的新矩阵,记为AT.在Matlab中矩阵转置运算的命令有两个,一个是“′”,另一个是“. '”．二者的区别是前者完成的是共轭转置,后者完成的是一般意义下的转置．对于实数矩阵,二者无区别,但是对于复数矩阵,二者有区别．

在Matlab 窗口中输入:

≫A=[1 0-1 2+i;-1 1 3 0; 0 5-1 4]; %定义数值矩阵

≫A′,A′

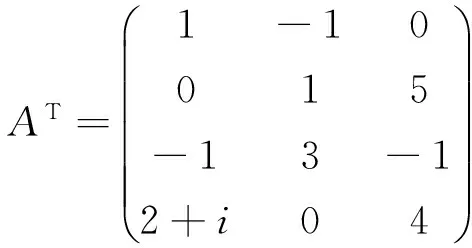
2.4 矩阵的逆

矩阵A的逆记为A-1. 在Matlab中矩阵逆运算是“inv(A)”, 其中A须为方阵,即行列相同的矩阵．

在Matlab 窗口中输入:

≫A=[-2 3-1;0 7 4;1 5 6]; %定义数值矩阵

≫ inv(A)

执行命令,即可得到所求结果为

即:

2.5 矩阵的秩

在教学中,通常向学生介绍利用化阶梯形矩阵的方法求矩阵的秩,比较繁琐．利用Matlab就简单的多,其命令为“rank(A)”,其中A为矩阵．

例8[5]设

求r(A).

在Matlab窗口中输入:

≫A=[1 1 2 5 7; 1 2 3 7 10; 1 3 4 9 13; 1 4 5 11 16]; %定义数值矩阵

≫ rank(A)

执行命令,即可得到所求结果为ans=2即矩阵的秩为2.

2.6 矩阵的迹

矩阵的迹是指矩阵主对角线元素之和,在Matlab中其命令为“trace(A)”,其中A为方阵．

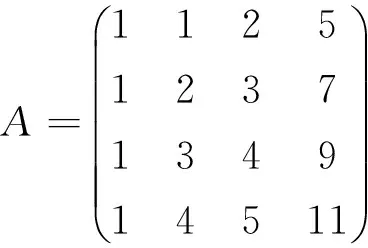
在Matlab窗口中输入:

≫A=[1 1 2 5; 1 2 3 7; 1 3 4 9; 1 4 5 11]; %定义数值矩阵

≫ trace(A)

执行命令,即可得到所求结果为ans=18 矩阵的迹为18.

2.7 矩阵的特征值、特征向量

在Matlab中,计算矩阵A的特征值和特征向量的函数是eig(A),最常见的调用格式有以下两种E=eig(A)和[V,D]=eig(A). 前者求矩阵A的全部特征值,构成向量E;后者求矩阵A的全部特征值,构成对角阵D,并求A的特征向量构成V的列向量．

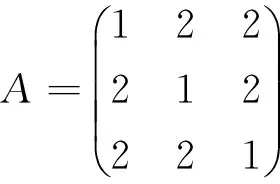
在Matlab窗口中输入:

≫A=[1 2 2; 2 1 2; 2 2 1]; %定义数值矩阵

≫E=eig(A),[V,D]=eig(A)

执行命令,即可得到所求结果为

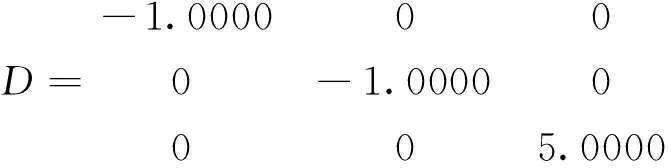
3 Matlab在线性方程组求解中的应用

求解线性方程组是线性代数的核心问题,贯穿课程始终．求解线性方程组的一般方法有克莱姆法则法、高斯消去法、逆矩阵法等．

例11[5]解方程组

解法1: 克莱姆法则法在Matlab窗口中输入:

≫A=[2 1-5 1; 1-3 0-6; 0 2-1 2; 1 4-7 6];

≫A1=[8 1-5 1; 9-3 0-6;-5 2-1 2; 0 4-7 6];

≫A2=[2 8-5 1; 1 9 0-6; 0-5-1 2; 1 0-7 6];

≫A3=[2 1 8 1; 1-3 9-6; 0 2-5 2; 1 4 0 6];

≫A4=[2 1-5 8; 1-3 0 9; 0 2-1-5; 1 4-7 0];

≫x1=det(A1)/det(A),x2=det(A2)/det(A),x3=det(A3)/det(A),x4=det(A4)/det(A)

执行命令,即可得到所求结果为

x1=3；x2=-4；x3=-1；x4=1

解法2: 逆矩阵法

在Matlab窗口中输入:

≫A=[2 1-5 1; 1-3 0-6; 0 2-1 2; 1 4-7 6];

≫b=[8; 9;-5; 0];

≫X=inv(A)*b

执行命令,即可得到所求结果为

4 结语

在线性代数的教学引入Matlab,可以克服传统板书教学中内容讲解抽象、学生学习积极性不高、缺乏兴趣等不足,可以使得枯燥的课堂生动有趣．但不能否认的是,Matlab在线性代数的教学中只可起到辅助的作用,平时的教学还是须以课本知识为主,不可本末倒置．

[1] 刘保柱,苏彦华,张宏. Matlab 7.0从入门到精通[M]. 北京: 人民邮电出版社, 2010.

[2] 刘春霞. MATLAB在线性代数教学中的应用[J].淮阴师范学院学报:自然科学版, 2015, 14(3): 248-251.

[3] 张雪峰. MATLAB仿真软件在线性代数课程中的应用研究[J]. 曲阜师范大学学报:自然科学版, 2016, 42(1): 42-46.

[4] 魏凤英. 基于矩阵求逆谈高等代数中的计算及MATLAB 实现[J].长春大学学报, 2013, 23(10): 1279-1281.

[5] 陈伏兵. 应用线性代数[M]. 北京: 科学出版社, 2011.

[责任编辑：李春红]

2016-11-25

国家自然科学基金资助项目(11301207);江苏省高校“青蓝工程”优秀青年骨干教师(2014)资助项目;江苏省“333高层次

刘蒙(1987-),男,安徽萧县人,副教授,博士研究生,研究方向为微分方程及其应用.E-mail: liumeng@hytc.edu.cn

G473

A

1671-6876(2017)01-0080-04

人才培养工程”与江苏省高校优秀中青年教师境外研修计划资助