浅谈利用“问题导向法”求解物体的密度

珠海市文园中学(519000) 柳兆胜 ●

浅谈利用“问题导向法”求解物体的密度

珠海市文园中学(519000) 柳兆胜 ●

“问题导向法”是从待求问题出发，利用公式搭建“待求问题”与“已知条件”的桥梁，主要特点是解题针对性强，更具有条理性．

初中物理;问题导向法;浮力

如何利用“问题导向法”求解物体的密度一直是学生较难解决的问题，笔者精选相应的例题利用“问题导向法”解决这类问题，在教学中取得了很好的效果．

“问题导向法”是从待求问题出发，利用公式搭建“待求问题”与“已知条件”的桥梁．主要特点是解题针对性强、更具有条理性．

浮力计算题综合了前面的密度、重力、压强公式以及平衡力的相关知识，对中考浮力计算题的命题多数偏向考查“称重法测量浮力”“漂浮”这两种情景，其中，计算物体的密度已经成为考查的热点．

一、利用称重法求解物体的密度

例1 在弹簧测力计下挂一圆柱体如图1所示，从盛水的烧杯上方某一高度缓慢下降，圆柱体浸没后继续下降，直到圆柱体底面与烧杯底部接触为止，如图2所示是圆柱体下降过程中弹簧测力计读数F随圆柱体下降高度h变化的图像．求圆柱体的密度是多少?(g=10N/kg)

“问题导向法”分析:

在正式解题时，我们只要逆着分析流程图，呈现解题步骤即可．

解 由图1．2可知，G柱=12N，圆柱体浸没时，F=4N

圆柱体浸没时，V柱=V排=8×10－4m3

答:圆柱体的密度是1．5×103kg/m3．

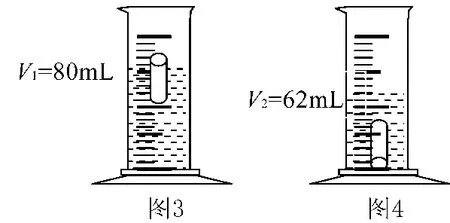
例2 小明为了测普通玻璃瓶的密度，他将玻璃小瓶口朝上漂浮在装有50mL水的量筒内如图3所示，此时水面与80mL刻度线相平;然后让小瓶口朝下沉没水中如图4所示，此时水面与62mL的刻度线相平．求小瓶的密度是多少?(g=10N/kg)

二、利用物体漂浮时，F浮=G物求解物体的密度

“问题导向法”分析

解题的顺序与例1相同，这里就不在赘述．

“问题导向法”采取了循序渐进的解题方略，初学者有了解题的附着点自然就不会束手无措．同时它的“低起点，小步子，快反馈”体现了从局部到整体的解题思想，高效地分配了学生的精力，增强了学生的解题能力．

G632

B

1008－0333(2017)02－0068－02