看似无“圆”却有“圆”——辅助圆巧解直线型问题

湖北省宜城城关中学(441400)) 李继芸 ●

看似无“圆”却有“圆”
——辅助圆巧解直线型问题

湖北省宜城城关中学(441400)) 李继芸 ●

近几年的中考题中出现了一种纯直线型几何题，但是利用直线型知识解答此类问题过于繁琐，甚至无法找到解题的思路和途径．遇这类问题我们要另辟蹊径，仔细分析题意，挖掘与圆的巧妙联系辅助于圆，便可化繁为简，化难为易，从而“圆”满地解决问题．

一、利用圆的定义作辅助圆

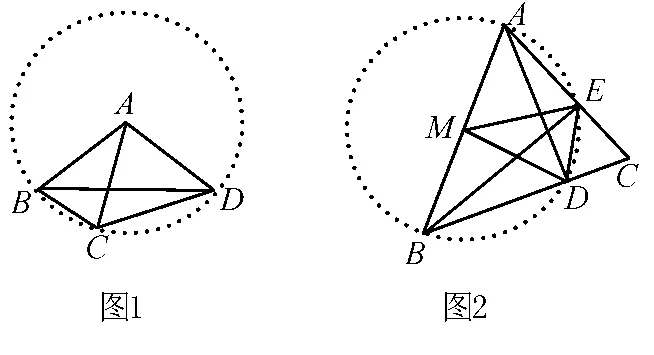
例题1 如图1，AB=AC=AD且∠CAD=76°，求∠CBD的度数．

解析 由AB=AC=AD，易联想到圆的定义画辅助圆，可知点B、C、D在以点A为圆心，AB为半径的圆上．从而依据同弧所对的圆周角是圆心的角的一半即可求解．

点评 当遇到有公共端点的几个条线段等长时，通常可根据圆的定义，以公共端点为圆心，等长的线段为半径构造辅助圆，利用圆的有关知识来解决问题．

二、利用直径所对的圆周角是直角构造辅助圆

例题2 如图2，△ABC中AD⊥BC于点D，BE⊥AC于点E，点M为AB的中点，求证:∠DME=2∠CAD．

解析 以点M为圆心，AM为半径作⊙M，由直角三角形斜边上的中线等于斜边的一半可证:AM=EM=DM =BM，所以A、E、D、B四点在⊙M上．利用同弧所对的圆周角(∠CAD)等于圆心角(∠DME)的一半即可求解．

例题3 抛物线y=ax2+bx－2经过点A(－1，0)B(4，0)交y轴于点C，动点P(m，n)在抛物线上，

(1)求抛物线解析式和顶点N的坐标;

(2)当∠APB为钝角时，求 m的取值范围．

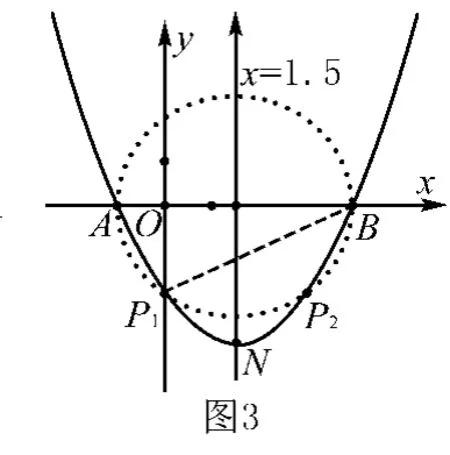
点评 遇到有公共斜边的两个直角三角形(直角可以在公共边的同侧或是异侧)的情况都可以利用直径所对的圆周角是直角构造辅助圆来解决问题．

三、利用同(等)弧所对的圆周角等于其所对的圆心角的一半构造辅助圆

例题4 在平面直角坐标系中，已知A(4，0)，B(－6，0)，点C是y轴上一个动点，当∠BCA=45°时，点C 的坐标是___．

解析 点C在y轴的正半轴上时，作△ABC的外接圆 O'．易得∠AOB=90°，则O'D=5，O'A=O'C

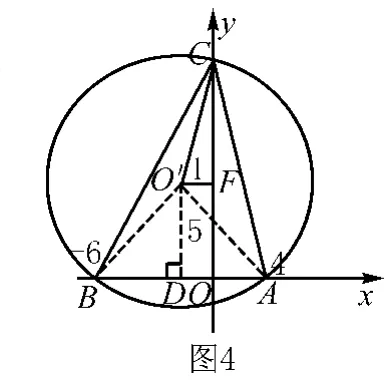
在Rt△O'FC中利用勾股定理可求出CF=7，因此得OC=12，故点C的坐标为(0，12)．

再利用对称性可求出当点C在y轴负半轴上时点C坐标为(0，－12)．

点评 作三角形的外接圆利用同弧所对的圆周角等于其所对的圆心角的一半，实现角的关系转化，利用圆的有关性质解决直线型问题可以起到事半功半的效果．

四、利用对角互补的四边形的四点共圆构造辅助圆

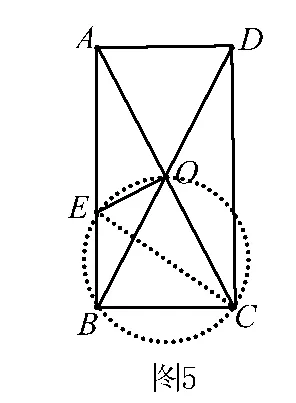
例题5 如图矩形ABCD的对角线BD、AC相交于点O，过点O作OE⊥AC交AB于点E，若BC=4，△AOE的面积为6，则cos∠BOE =___．

解析 连接CE，由OE为线段AC的垂直平分线证得AE=CE．由OA=OB易证△AOE的面积等于△COE的面积，故得△ACE的面积为12．因为．所以AE=CE=6．

由∠COE+∠CBE=180°则可证点O、E、B、C四点共圆，因此可证∠BOE=∠BCE，所以

点评 求锐角三角函数值，通常需要将已知角转化到直角三角形中．利用对角互补的四边形的四点共圆构造辅助圆，利用同弧所对的圆周角相等实现角的转化是常用的方法之一．

G632

B

1008－0333(2017)02－0004－01