2016年宁波中考压轴题解法探究及教学反思

浙江省宁海县桃源中学(315600) 王 伟 ●

2016年宁波中考压轴题解法探究及教学反思

浙江省宁海县桃源中学(315600) 王 伟 ●

2016年宁波中考数学试题第26题压轴题，借助特殊平行四边形的旋转，呈现角与角，边与边之间的不变和变的辩证关系，实现边与角，未知向已知的转化，此题着重考查学生综合应用所学知识解决问题的能力．因此，在数学教学中，应探究多种不同的解法，这种殊途同归的解题方法可以拓宽学生的理解，使思维向多方向发展，有利于学生发散思维流畅性的形成和发展．下面结合问题，探究第三，第四问的几种解法，供参考．

中考压轴题;解法探究;一题多解;思维突破

题目26 如图1，在平面直角坐标系中，O为坐标原点，点A的坐标为(5，0)，菱形OABC的顶点B，C都在第一象限，将菱形绕点A按顺时针方向旋转得到菱形FADE(点O的对应点为点F)，EF与OC交于点G，连结AG．

(3)求证:GA平分∠OGE;

(4)连结BD并延长交x轴于点P，当点P的坐标为(12，0)时，求点G的坐标．

对于第三问证明角相等例举三种解法．

解法一 如图2．

过点A作AN⊥EF，AM⊥OG垂足分别是M，N．

由旋转可得∠AOM=∠F，OA=AF．

∵∠AMO=∠ANF=90°，

∴△AOM≅△AFN，∴AM=AN．

∴GA平分∠OGE．

解法二 如图2，过点A作AN⊥EF，AM⊥OG．

∵菱形OABC≌菱形AFEB，EF=OC，

由面积相等可得AM=AN，∴GA平分∠OGE．

解法三 如图3，∵∠COA=∠EFA，∴O，F，G，A四点共圆．∵∠EGA=∠OFA，∠OGA=∠OFA，∵AF=OA，∴∠AOF=∠OFA，∴∠OGA=∠EGA．

对于第四问求点G坐标例举十种解法．

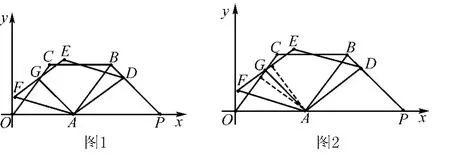
解法一 如图4，分别延长AG，BC交于点M，作GH⊥OP，垂足为H，连接OF．

解法二 如图5，过B作BH⊥OP，垂足为H，利用∠COA=∠BAP，得出

∴AH=4，BH=3，HP=3，

∴∠BPA=45°．

由解法一知AG∥BP，

∴∠OAG=∠APB=45°．

∴lAG:y=－x+5．与直线x联立方程组求出交点

解法三 如图6，过点G作GQ⊥OP，过B作BH⊥OP，垂足分别Q，H．在解法二中求出∠OAG=45°后，也可设OQ=3a，CQ=4a，则7a=5，求出，从而得到G

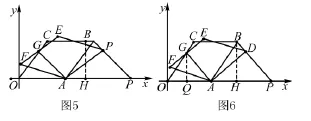
解法四 如图7，连接OF，过点B作BH⊥OP，过D作DN⊥OP，过F作FM⊥OP，垂足分别为H，N，M

由解法二得∠BPA=45°．设DN=NP=x，由勾股定理可求得DN=NP=3，从而得出D(3，4)．

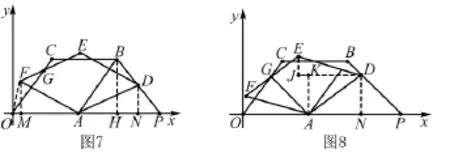
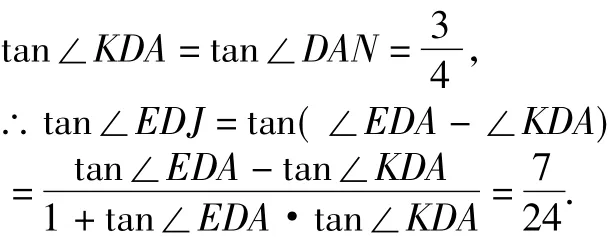
以下解法同解法四．

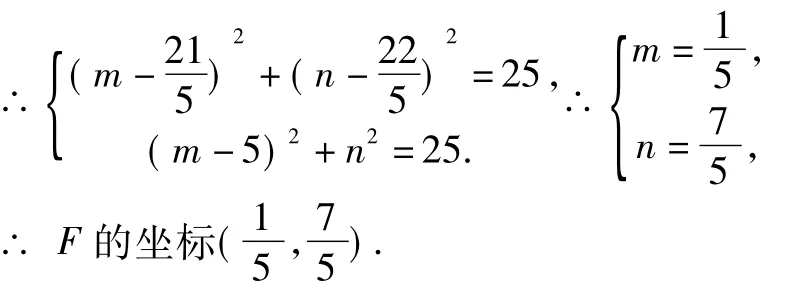
解法七 如图1，求F的坐标也可利用菱形对角线互相平分的性质．由解法五知

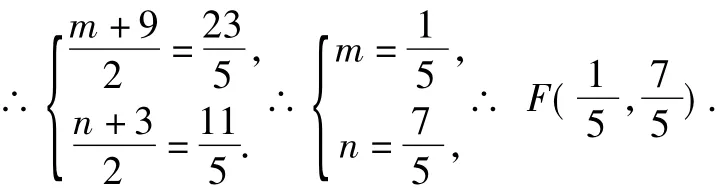
解法八 如图9，过G作GQ⊥OP，BH⊥OP垂足分别为Q，H．

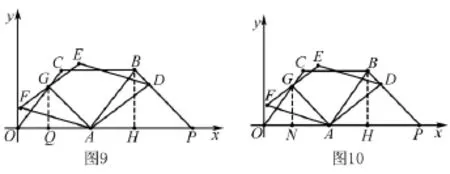
解法九 如图10，作GN⊥OP，BH⊥OP垂足为N，H．

由解法二已得知∠BPA=45°．在△ABP中利用正弦定理可求得，从而得在△OGA中．从而可得

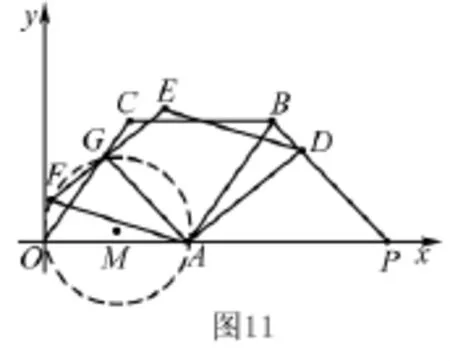
∵O，F，G，A四点共圆，利用圆方程求解．

设圆M的方程为 ( x－a)2代入，可求出圆方程为，将O，A，F三点

教学反思 以上的多种解法综合利用全等，平行，相似，勾股定理，锐角三角函数，四点共圆，正弦定理等核心知识解决问题．每一种解法的延伸都是源于平时积累的知识，因此在平时的教学中，教师要善于引导学生从多角度，多层次审视问题，多方位寻找解题方法．对于第三问有效设置台阶，为后续的研究做好铺垫，对于第四问求点G的坐标，需要学生对所学的知识灵活运用，融会贯通，使学生多角度去思考，培养学生发散思维的流畅性．解法一解法八思路:利用相似求出OG的长度，再结合锐角三角函数求出G的坐标．解法二思路:利用直线OC和直线AG的交点求出点G坐标．解法三的思路:用解法二中∠OAG =45°，求出OG，GA的长度，从而得出G的坐标．解法四，五，六，七的思路:利用直线EF与OC的交点求出点G的坐标．解法九思路:利用正弦定理求出AG的长度，再结合锐角三角函数求出点G的坐标．解法十:利用圆方程和直线CO的交点求出点G的坐标．初中阶段求一个点的坐标，利用交点求解是一种比较常用的方法．

中考压轴题已经由单纯的知识叠加型转化为知识，方法和技能综合型，这也是完全符合课改的要求．由于压轴题考查的知识点较多，综合性较强，覆盖面广，关系复杂，思路难觅，解法灵活，常常令一些学生束手无策．因此需要教师在教学过程中正确引领学生走进压轴题的世界，为提高学生压轴题的得分率，对学生解答压轴题方法策略上的指导是必要的．根据课改的目标，压轴题的一般教学策略可关注以下几个方面:1．审题;2．问题转化;3．数学思想方法;4．一题多解;5．思维自我监控;6．解题后的反思．教师在教学过程中可以制定一些具体的教学策略，笔者认为在教学过程中教师应该注重如下几个具体策略:1．引导学生认真审题挖掘隐含条件．2．引导学生数形结合．3．引导学生用识别基本模型，关注基本图形的特征．4．引导学生转化问题．5．引导学生在解题过程中思维自我控制．6．引导学生一题多解和多法归因．7．引导学生解题后有效反思．8．引导学生适当变式．

解题探究重在培养思维能力，意在孕育探究精神，久而久之，便形成可持续发展的数学解题技巧和数学解题能力．

［1］王伟．数学变式百例精讲［M］．浙江:宁波出版社，2006

［2］蔡卫兵．2015年浙江省宁波卷第26题解法探究及反思［J］．中学数学教育，2016(6)

G632

B

1008－0333(2017)02－0007－02