初中几何求最小值的技巧

贵州省沿河县第六中学(565302) 杨再发 ●

初中几何求最小值的技巧

贵州省沿河县第六中学(565302) 杨再发 ●

一、用点到线的距离垂线段最短来求

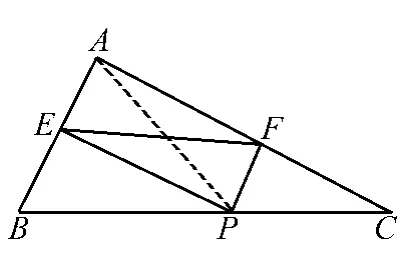
例1 如图，在△ABC中，AB=3、AC=4、BC=5，点P为边BC上的一个动点，且PE⊥AB于E、PF⊥AC于F，求EF的最小值．

解 连接AP．AB=3，AC=4，BC=5，32+42=25，52=25，即AB2+AC2=BC2，所以△ABC是Rt△，即∠BAC=90°．因为PE⊥AB于E、PF⊥AC于 F，所以四边形AEPF是矩形，所以EF=AP．要求EF的最小值，就是求AP的最小值．即就是求点A到BC的最小值．当AP⊥BC时，AP最小，所以过A作AP⊥BC于P如图．

二、用两点之间线段最短来求

解决线段和最小值的问题经常与轴对称联系起来，通过作对称点把要相加的线段进 行等量代换，放置在同一条直线上成为一条线段．

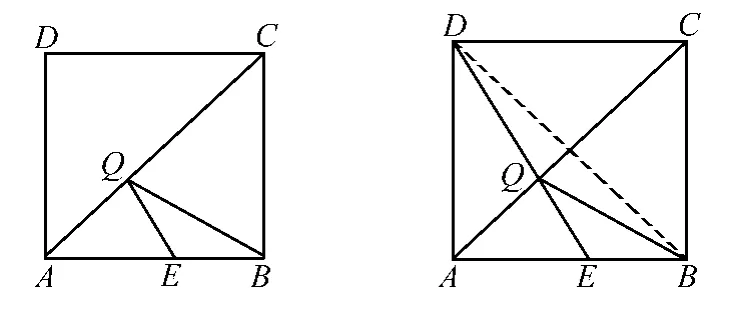
例2 如图，在边长为4的正方形ABCD中，E是AB上的一点，且AE=3，点Q为对角线AC上的一个动点，求△BEQ周长的最小值．

解 因为△BEQ的周长=QE+QB+BE，而BE的长度已固定．所以求△BEQ周长的最小值，就要使QE+QB的值最小．将QE、QB转化在一条线段中，根据两点之间线段最短来解．因为正方形是轴对称图形，所以B、D是关于AC对称．如图，连接DE交AC于点Q，连接QB．则QB =QD，所以QE+QB=QD+QE=DE．因为AD=AB=4AE =3，所以BE=1．则QD +QE=QB+QE=5，所以△BEQ的周长=QE+QB+BE =5+1=6，所以△BEQ周长的最小值是6．

三、用三角形两边之和大于第三边来求

例3 已知:如图在四边形ABCD中，AD、BC不平行，F、E分别是AB、CD的中点，若EF=8，求AD+BC的最小值．

解 连接BD，取BD的中点G，连接EG、FG．因为E、F分别是CD、AB的中点，所以EG、FG分别是△BCD、△ABD的中位线．即在△EFG中，因为EG+FG＞ EF．

当E、G、F三点共线时取得最小值，即EG+FG≥EF．因为EF=8，所以BC+AD≥8，则BC+AD≥16，所以AD +BC的最小值是16．

G632

B

1008－0333(2017)02－0006－01