深圳中考之最值归纳

广东省深圳市龙岗区龙城初级中学(518100) 杜春联 ●

深圳中考之最值归纳

广东省深圳市龙岗区龙城初级中学(518100) 杜春联 ●

在初中的数学学习过程中，经常会遇到求最值的问题，这也是学生感觉比较难处理的问题，甚至很多学生无从下手，原因是对问题的基本模型不了解，如果把无关紧要的东西都去掉，让题目原形毕露，回到最基本的数学模型，问题就容易解决了，突破口是线段公理及其推论即两点间线段最短和三角形的两边之和大于第三边，以下是深圳中考几种常见的最值类型．

深圳;数学中考;最值

一、基本模型一 两定点在定直线同侧，求两线段和的最小值

已知A、B两点在直线l的同侧，在直线l上找一点P，使PA+PB的值最小．

分析 根据对称性先找到点P然后根据线段公理证明最小值．作A点关于直线l的对称点A'，连接A'B交直线l于点P，此时PA+ PB的值最小．由对称性可知PA=PA'，∴PA+PB=PA'+?PB=A'B．

如果在直线l上还存在一点P'，则

P'A+P'B=P'A'+P'B＞A'B．∴当A'，P，B三点在一条直线上，使PA+PB的值最小．

例题分析

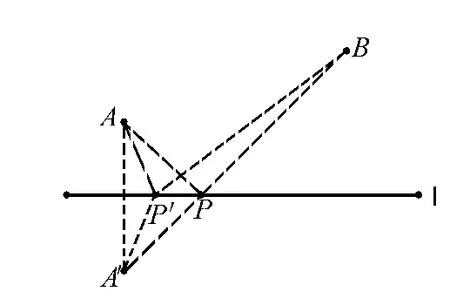
1．如图1，在平面直角坐标系中，A(2，－2)，B(4，2)两点，P是直线x=1上的动点，则PA+PB 的值最小是___．

分析 两定点在定直线同侧，求两线段和的最小值，属于基本模型一．

2．如图2，MN是半径为1的圆O的直径，点A在圆O上，∠AMN=30°，B为弧AN的中点，P是直径MN上一动点，则PA+PB 的最小值为___．

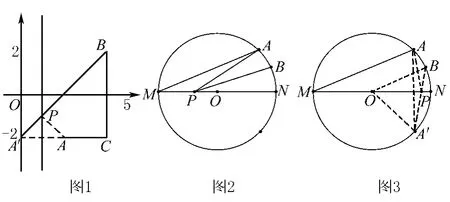
分析 两定点在定直线同侧，求两线段和的最小值，属于基本模型一．

如图3所示，A与A'关于MN对称，连接A'B交MN于点P，则PA+PB=PA'+PB=A'B．

∵∠AMN=30°，B为弧AN的中点，∴∠BON=30°∠A'ON=∠AON=60°，∴∠A'OB=90°．由勾股定理可，得:

二、基本模型二 两定点在定直线同侧，求两线段差的最大值

PA－PB =AB，此 时PA－PB的值最大，这类题在深圳中考出现的机率少一点．

三、基本模型三 两定点在定直线两侧，求两线段差的最大值

已知如图4，A、B两点在直线l的两侧，在直线l上找一点P，使的值最大．

利用对称性，把模型三转换成模型二，过B点作关于直线 l的对称点 B'点，连接 AB'交直线 l于点 P，则

例题分析 如图6，梯形ABCD中，AD∥BC，BE平分∠ABC，且BE⊥CD于E，P是BE上一动点P，若BC=6， CE=2DE，则的最大值是 ．

分析 A、C两点在直线BE的两侧，在直线BE上找一点P，使的值最大，与模型三相同，因此要先找期中一个点关于直线BE的对称点，再把对称点和另一个点连接起来与直线BE相交即可求出．

因为已知条件中BE⊥CD，所以考虑作C点关于直线BE的对称点F，连接AF，则就是所求的．

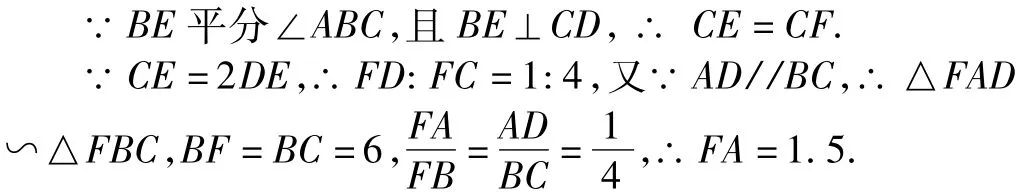
变式 如图8，抛物线y=x2－2x－3与x轴交于A、B两点(点A在点B左侧)，若直线PE为抛物线的对称轴，抛物线与y轴交于点D，点M、Q为直线PE上动点．

(1)在对称轴上是否存在一点M，使三角形ADM的周长最小?若存在，求出这个最小值及点M的坐标，若存在，请说明理由．

分析 (1)三角形ADM的周长=AD+DM+MA符合基本模型一，两顶点在定直线同侧，在直线上找一个点，使得到两个定点的距离之和最小．即作D点关于PE的对称点D1，连接AD1交PE于点M，三角形ADM的周长=AD+DM+MA =AD+AD1取值最小．

四、基本模型四

已知一个定点两条定直线，在直线上找两个点使得定点到两动点的距离之和最小．

如图9，已知∠A和这个角内的已知点P，求作直线BC交∠A的两边于B、C，使△PBC的周长最小．

分析 分别作点P关于角两边的对称点P1，P2，连接P1P2交角两边于B、C两点，则△PBC的周长=PC+CB+BP =P2C+CB+BP1=P1P2．如果还存在另外两点C1，B1，则△PB1C1周长=PC1+C1B1+B1P=P2C+C1B1+B1P1＞P1P2，所以△PBC周长的最小值为P1P2．

变式分析 如图11，抛物线y =x2－2x－3与x轴交于A、B两点(点A在点B的左侧)，直线l与抛物线交于点A、C，其中点C的横坐标为2，若直线PE为抛物线的对称轴，抛物线与y轴交于点D，直线AC与y轴交于点Q，点M为直线PE上一动点，则在x轴上是否存在一点N，使四边形DMNQ的周长最小?若存在，求出这个最小值及点M的坐标，若不存在，请说明理由．

分析 四边形DMNQ的周长最小，因为DQ是定值，所以要四边形DMNQ的周长最小，则DM+MN+NQ+QD的值最小作Q点关于x轴的对称点Q1，D，C刚好关于抛物线的对称轴对称，连接Q1C分别交x轴及对称轴于点N、M，则NQ=NQ1，MD=MC，所以四边形DMNQ的周长=DM+MN+NQ+QD=CM+MN+NQ1+QD=Q1C+QD取最小值．

G632

B

1008－0333(2016)32－0022－02