例谈“数学素养”*

□ 郜舒竹 常 鑫

例谈“数学素养”*

□ 郜舒竹 常 鑫

关于“数学素养”可以理解为：人能够成功实施与数学相关的行动所具备的条件。在一节主题为“密码中的规律”的展示课中，学生针对兰福德问题的探索过程中，经历了在观察过程中感受规律并描述规律的活动，面对复杂问题经历特殊化的思考活动，解决问题之后运用从特殊到一般的思维方式经历问题生问题的活动，遇到问题难以解决的困难时，经历运用直觉的思维方式进行猜想的活动，以及对于数学问题追求其完美解决的活动。凡此对相关数学素养的养成会有所裨益。

素养 数学素养 学习活动

如果把素养理解为“人之本身”的修养，那么“数学素养”就可以理解为数学专业工作者或数学家所拥有的专业修养。依据这样的理解很难演绎出“数学素养”作为一个概念所包含的内容（外延），当然也就无法将数学素养与学生学习数学的活动建立联系，因此作为数学教师也就无法将其落实到日常的数学教学及其评价之中。究竟应当如何理解数学素养？如何在数学教学中真正实现“素养导向”？这些就成为了亟待回答的问题。

一、如何理解“数学素养”

如果把对素养的理解指向“人之行动”，把“人的素养”与“人的行动”联系在一起，也就是把素养看作是人能够成功行动的先决条件，那么素养这一具有抽象性的概念就具体化并且行为化了。据此，数学素养就可以演绎为是人能够成功实施与数学相关的行动所具备的条件。其中的行动可能是对事物的观察，对概念的理解，可能是数学中的计算，对数学符号的使用，也可能是应用数学知识解决实际问题，等等。这样的素养不仅包括数学知识和技能，同时也包括诸如情感、态度以及经验、方法等。

在“经济合作与发展组织①英译：Organization for Economic Co-operation and Development（以下简称OECD）所开展的“国际学生评价项目②英译：The Programme for International StudentAssessment（以下简称PISA）”的数学素养测试中，明确指出：“所测试的数学素养是针对15岁学生在义务教育结束时，对于日常生活活动中使用数学的能力。”因此，PISA所说的数学素养实质上是与“用数学”的行动联系在一起的，其测试内容并不是与数学相关的全部行动及其素养。

综上，如果把数学教学的目标定位于素养导向，那么就应当把数学素养理解为学生在学习数学过程中，经历各种与数学相关的学习活动中所能够习得的素养。鉴于数学素养与数学学习活动的这种关系，那么素养导向数学教学的基本原理就应当是创造机会和环境，让学生“亲身经历”与数学相关的学习活动。接下来的问题是学生在学习数学的过程中可能经历什么样的活动。这样的问题，很难作出全面、准确的回答，因此需要通过具体案例进行归纳并且积累。

2016年11月在杭州举办的“第一届西湖之秋全国小学数学课程与教学研讨峰会”上，有一节由北京市朝阳区南磨房中心小学常鑫老师执教的主题为“密码中的规律”的展示课。本节课的核心内容选用的是组合数学中一个著名的排列问题：将六个数字：1，1，2，2，3，3排成一排，使得两个1之间有一个数字，两个2之间有两个数字，两个3之间有三个数字。虽然这是专业的数学问题，其实是源于年幼儿童玩积木的游戏。

这一问题最早于1958年10月刊登于英国一个名为《Mathematical Gazette》的期刊上。提出问题的作者是苏格兰的一位名叫杜德利·兰福德（Dudley Langford）的数学家，因此这个问题被后人称为“兰福德问题（Langford Problem）”。兰福德发现这一问题的灵感来源于对年幼儿子玩弄彩色积木的观察。（见图1）

图1 儿童搭积木示意图

一共6个木块，其中红色、黄色和蓝色各有2个，自下而上摆成一列后发现，2个红色木块之间有1个木块，2个黄色木块之间有2个木块，2个蓝色木块之间有3个木块。兰福德改用数字1、2、3分别代表红、黄、蓝三种颜色的木块，就得到了一个有规律排列的六位数：312132。

无论是6个木块还是6个数字，排成一排可以有许多各式各样的排法。能够注意到其中的“312132”，实际上就是感知到了其中的某种规律，这一规律可以表述为：两个几之间就有几个数。也就是1和1之间、2和2之间以及3和3之间数字个数的一种共性，正是这样的共性沟通了不同对象之间的联系，使得不同对象共同构成有机的整体。这种不同对象之间的联系就是通常所说的规律，因此可以说，“312132”是一个按照一定规律排列的六位数。

这样“异中求同”的想法可以应用于对许多事物的认识，比如几何中对圆形的认识，如果在圆周上随便选取两个不同位置的点，其共同的属性是，到圆心的距离都一样。正是这样的“异中之同”沟通了圆周上不同位置点之间的联系，进而决定了圆形的形状，使得圆形成为了一个有规律的图形。

学生在学习数学的过程中，经常经历这样“异中求同”以及“动中求静”的观察与思考，对于逐步养成与“观察”以及“理解”行动相关的素养，无疑会有所裨益。

二、从特殊到一般

在发现了有规律排列的六位数“312132”后，接下来要思考的问题是，符合规律的排列方法是不是唯一的？如果不是唯一的，如何找到所有符合这样规律的答案？回答这样的问题具有一定的复杂性，数学家通常的思路是采用“特殊化（Specialization）”的方法，也就是选择一个相对容易的地方入手，这种相对容易的地方往往处于“极端情况”。

上面问题中两个“1”之间只能摆放一个数字，因此就是一个相对容易的极端情况。这个数字只有2和3两种可能性，可以逐一进行试验。如果两个1之间是2，就可以排出三个数字：121，这时左右两边只能是两个3，即排出了五个数字：31213，还剩下一个2，放在左右两边都可以满足要求：231213、312132，因此就得到了本题的两个答案。另外一种可能性是两个1之间是3，排出三个数字为：131，这时在右边只能排2，即1312，这样另一个2就无处可放了，说明两个1之间不能是3。所以本题的答案只能是：231213和312132。

解决这一问题还有一个思路，是从最大的极端情况入手，即从两个3之间进行思考。（见图2）

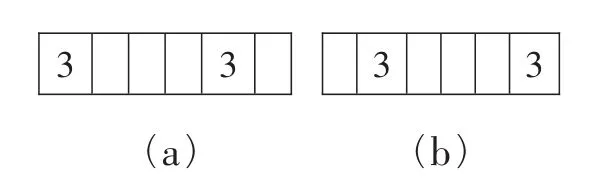
图2 六位数排列第一步示意图

虽然两个3之间需要摆放三个数字，较为复杂，但两个3所处的位置的可能性较少，只有图2中（a）和（b）两种可能，因此也相对容易入手。如果两个3按图2（a）方式摆放，那么左数第二个位置不能是2（否则另一个2与右数第二个位置的3重叠），因此只能放1。因此得到如图3的排列。

图3 六位数排列第二步示意图

剩下两个空位恰好放置两个2，因此得到答案为：312132。对于图2（b）的情况也可以用完全相同的方法得到答案为：231213。

312132和231213这两个答案从形式上看是不一样的，但在数学家眼里两者没有区别，因为无论哪一个，如果从右向左看与另外一个答案就完全相同，因此两者仅是观看顺序的不同，而没有本质的差别。所以问题的答案可以认为是唯一的。

像上面这样面对复杂问题所采用的“特殊化”的方法，实际上就是辩证唯物主义方法论中“化繁为简、化难为易”的具体体现。自然应当是学生学习数学过程中应当习得的数学素养。

至此，对于有规律地排列六位数的兰福德问题可以说已经得到解决。但对于问题的思考并没有停止，自然而然地应当进一步去想有没有类似的问题，或者具有更广泛意义的问题。这种思维方式通常叫作“一般化（Generalization）”，一个相对具体的问题解决后，总要设法将其推广到更大的范围，使其具有更广泛的意义。

如果把本题的六个数改为八个数：1，1，2，2，3，3，4，4，将这八个数排一排，使得两个几之间就有几个数。用前面的方法不难得到答案为：23421314和41312432。如果不考虑观看顺序的差别，那么这两个答案同样也可以看作是一样的，也就是对于有规律地排列八位数的兰福德问题，答案也是唯一的。

从旧的问题去发现并提出新的问题，如此反复进而形成“问题链”，应当说是数学发展历史中常见的现象。当然也应当成为学生在学习数学过程中应当经历的重要活动。进而逐步形成“问题生问题”的意识，应当说也是数学素养的一个方面。

三、直觉的力量

在前面问题解决的基础上，进一步需要思考的问题是：如果最大数改为两个5的十个数字：1，1，2，2，3，3，4，4，5，5，怎样排出满足要求的十位数？这样的叙述，是延续了前面的思维方式，是在排法“存在”的前提下提出来的。但是经过反复试验，怎么也排不出来。面对这种“排不出来”的困境，应当想到会有两种可能性。

●第一是排法存在，还没找到；

●第二是排法根本不存在。

究竟哪一种可能性比较大，目前并没有足够的理由作出准确的判断，如果相信“排法存在”，下一步的工作将是继续努力寻找；如果相信“排法不存在”，那么下一步努力的方向就不再是寻找排法，而是设法说明“不存在”的理由，也就是证明不存在。

人在遇到困难或者身处困境的时候，既不应当气馁而退缩，也不应当盲目而蛮干。智慧的表现应当是能够全面地列举有可能摆脱困境的各种可能性，并对各种可能性的大小作出判断。像这样对可能性的思考，以及在没有足够证据的情况下所作出判断的思维过程，就是数学家经常使用的“直觉（Intuition）”思维，由此获得的判断叫作“猜想（Con⁃jecture）”。

如果猜想排法不存在。接下来就要去说明“排法”不存在的道理。可以采用“填格”的办法，将五个方格和五个圆圈相间地排一排。（见图4）

图4 十位数图形排列示意图

对两个相同的偶数，比如“2，2”来说，因为两者之间间隔偶数个数字，因此无论怎样排，必然是一个放在□中，另一个放在○中，一共有两对偶数“2，2”和“4，4”，所以这四个数字就占据了两个□和两个○，还剩下三个□和三个○。

对于两个相同奇数来说，无论怎样排，必然放在同样的图形内，要么都是□，要么都是○。而现在还剩下三对奇数：“1，1”“3，3”“5，5”，如果两个1占据两个□，两个3占据两个○，剩下一个□和一个○，两个5就无法放置在相同图形内了。

因此可以得出结论，对最大数为两个5的十个数来说，这样的排法是不存在的。用同样的方法也可以说明对于最大数为两个6的12位数，满足要求的排法也是不存在的。证明了“不存在”，在数学研究中也被认为是解决了问题。现在可以说针对兰福德问题，已经解决了最大数分别为3、4、5、6的情况。

排法有时存在，有时不存在，数学家通常就会叙述出涵盖特殊情况的一般问题。对于2n个数：

1，1，2，2，3，3，……，n，n

前面问题的结果说明，当n=3和n=4时，满足要求的排法存在，而且在不考虑观看顺序的情况下，排法是唯一的。当n=5和n=6时，满足要求的排法不存在。进一步需要研究的问题是：当n满足什么条件时，这样的排法存在？对于排法存在的情况，一共有多少种不同的排法？

用与前面类似的方法可以得到结论为：如果n是4的倍数或者是被4除余数为3的整数，那么排法存在。如果n是被4除余数为1或2的整数，那么排法不存在。

比如，如果n=5，被4除的余数为1，排法不存在。如果n=6，被4除的余数为2，排法也不存在。如果n=7，被4除的余数为3，排法存在，比如73161345726425就是其中的一种排法。同样n=8是4的倍数，排法存在，一种排法为：627425864375 1318。

四、真实的问题带来真实的学习

兰福德问题自1958年出现后，吸引了许多人的关注。已故美国著名的数学游戏专家马丁·加德纳（Martin Gardner，1914年10月21日—2010年5月 22日）分别在1967年11月、12月以及1968年3月的《科学美国人（Scientific American）》期刊上，三次讨论过这个问题。这一问题目前已经成为一些“组合数学”和“数论”教科书中的经典例题。由中国数学会普及工作委员会1986年举办的“第一届全国数学冬令营数学竞赛”中，也采用了这一问题对于“n=1986”的情况作为试题之一。

迄今为止，兰福德问题并没有得以彻底解决，目前对于排法存在的情况，如何找到全部排法仍然是个难题。一些数学家为了追求完美的结论，仍然在探索着。比如对于n=7的情况，已经发现有26种不同的排法。（见图5）

图5 n=7兰福德问题排法

兰福德问题是数学界真实出现的问题，将这种真实的问题引入数学课程，自然会给学生带来真实的学习活动。选用兰福德问题作为数学课程内容主要基于三点理由。

第一是对国家课程中所规定的相关内容进行补充和完善。在国家课程“数与代数”领域中有“探索规律”的内容，而教科书中所出现的相关内容多为观察方向单一或者循环排列的数列。而兰福德问题中的规律更倾向于“图案（Pattern）”的特征，观察的着眼点在于相同数字之间数字的个数与这两个相同数字之间的相等关系，与诸如“112233”这种从左到右有规律的排列，或者“123123”这种从左至右同时具有循环规律的排列，都是不一样的。因此让学生经历这样内容的学习，有益于拓展学生对于探索规律这一课程内容的视野。

第二个理由是兰福德问题的思考与解决过程中，蕴含着丰富并且真实的与数学研究相关的活动。比如在观察过程中感受规律并描述规律的活动，面对复杂问题经历特殊化的思考活动，解决问题之后运用从特殊到一般的思维方式经历问题生问题的活动，遇到问题难以解决的困难时，经历运用直觉的思维方式进行猜想的活动，以及对于数学问题追求其完美解决的活动。学生经历如此丰富的活动，自然有益于数学素养的养成。

第三个理由是兰福德问题认知起点较低，富于趣味性和操作性。马丁·加德纳曾经在《科学美国人》期刊中提及，可以用扑克牌直观操作探索兰福德问题。比如对于“312132”的排列，可以用扑克牌表示为图6的形式（图中“A”代表数字“1”）。

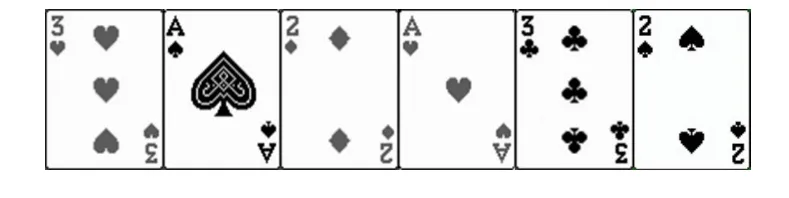
图6 扑克牌排列示意图

在实际教学中，为了让学生感受到此类问题的实际意义，还可以针对现实生活中，人们在使用诸如支付宝、微信钱包、网上银行等活动中，需要编制既私密又易记的密码的需求，让学生感受到这一内容的实际应用，进而产生探索的动机。

整个问题的探索过程可以分为问题提出、问题解决、问题推广以及总结反思几个阶段，教师可以针对学生的年龄特点进行更有针对性的教学设计。

[1]郜舒竹.用归纳的方法理解“素养”[J].教学月刊·小学版（数学），2017，1/2.

[2]César Sáenz.The Role of Contextual，Conceptual and Procedural Knowledge in Activating Mathematical Competencies（PISA）[J]Educational Studies in Mathematics，Vol.71，No.2（Jun.，2009），pp.123～143.

[3]Langford，C.D.Problem[J].Mathematical Gazette，Vol.42，No.228（Oct.，1958），p.228.

[4]Gardner，M.Mathematical Magic Show：More Puzzles，Games，Diversions，Illusions and Other Mathematical Sleight-of-Mind from Scientific American[M].New York：Vintage，pp.70 and 77～78，1978.

[5]P.R.Lloyd.Letter to editor[J].The Mathematical Gazette，Vol.55，No.391（Feb.，1971），p. 73.

（首都师范大学初等教育学院 100048北京市朝阳区南磨房中心小学 100124）

2016年北京市科技计划面上项目“数学的教育形态研究”（KM201610028020）。