基于二阶包络逆EMD算法改进与实现
2017-04-11何经伟胡维平莫家玲
何经伟, 胡维平, 莫家玲
(广西师范大学 电子工程学院 广西多源信息挖掘与安全重点实验室,广西 桂林 541004)
基于二阶包络逆EMD算法改进与实现
何经伟, 胡维平, 莫家玲
(广西师范大学 电子工程学院 广西多源信息挖掘与安全重点实验室,广西 桂林 541004)
在分析经典EMD(Empirical Mode Decomposition)和高阶极值点逆向筛分EMD方法的基础上,提出了一种基于二阶包络逆EMD的改进方法。该方法结合标准EMD与逆EMD的良好属性,采用一阶、二阶包络,通过给定条件在筛分过程选择最优包络均值进行筛分。实验结果表明:该方法适用于分解频率差值较低的多分量信号且减小高频分量误差;有效地减小估计误差及抑制多余IMF分量;以最优包络作为筛分包络,EMD分解效果更佳。
标准EMD;逆EMD;二阶包络逆EMD
Hilbert-Huang变换是 HUANG等[1]提出的一种用于非平稳、非线性信号的自适应处理方法。它突破了传统的基于短时傅里叶变换的信号处理方法,是信号处理方法上的一次飞跃。HHT主要有两个过程:经验模态分解(EMD)和Hilbert变换。EMD目的是为了得到IMF,以便进一步利用Hilbert变换进行分析。在EMD算法中,信号的极值点信息在分解过程中至关重要。极值点信息的有效利用及EMD分解算法的改进研究,一直吸引着学者们。徐冠雷等[2]通过分析研究二级极值点结构,提出了从多分量到单分量用EMD分解的极值点判断准则。 KOPSINIS等[3]提出了一种基于差值点选择的EMD分解方法。 KOPSINIS 等[4]提出了一种基于特定最优极值点的启发式搜索的改进EMD分解法。XU等[5]提出了限邻域均值的EMD分解法。LI等[6]通过利用高阶极值点信息,提出了一种由最优包络均值逆向筛分的EMD分解法。
本文首先介绍两种包络方式的EMD分解方法,分析其存在的优势及局限性,然后提出一种新的EMD方法并通过大量实验验证该方法的有效性。
1 经典EMD算法的基本原理
对给定信号x(t)的EMD分解算法[7]具体流程如下:
(1) 首先确定给定信号x(t)所有的局部极大值点以及极小值点,通过利用三次样条插值法通过极大值点(极小值点)分别拟合出上u(t)(下1(t))包络曲线。计算上下包络均值m(t)=(u(t)+1(t))/2,将原始信号x(t)减去m(t)得h(t),即:h(t)=x(t)-m(t)。
(2) 判断h1(t)是否满足IMF的两个条件,如果满足,h1(t)就是筛选出来的第一个本征模态函数分量,如果不满足,把h1(t)作为原始数据继续重复进行上述步骤一操作,直到h1(t)满足IMF分量的条件。这样经过多次筛选我们将得到第一个IMF分量C(t)。
(3) 将C(t)从原始信号x(t)分离出来得到剩余信号:r(t)=x(t)-C(t)
(4) 我们将剩余信号继续进行上述一至三步骤操作,这样得到第二个本征模态函数分量。如此重复K次,就会得到满足IMF条件的K个IMF分量,以及一个最终残余分量r(t)。残余分量是一个不为零的分量,其代表信号的趋势。此时满足EMD终止准则,筛选结束。我们将信号分解结果可表示如下:
(1)
式中x(t)为原始信号,n表示IMF分量的个数,cj(t)为第j个IMF分量rn(t)为残余分量。
经典EMD通过采用三次样条插值拟合一阶包络,通过多次筛分的方式将复杂信号分解成各个本征模态函数。该方法具有普遍适用性,不管是复杂实际信号,还是多分量信号,都具有较好的分解效果,但是该方法对高阶包络没有一定预测能力,会产生较大的估计误差,在分解过程中,不能有效避免多余的IMF分量。
2 逆EMD算法的基本原理
逆EMD分解中的“逆”并非完全意义上的逆,而是因为它是一种基于高阶极值点的EMD方法。它利用n阶极值点信息构造成n阶最优包络通过逆向筛分的方式获得各个本征模态函数。
原逆EMD算法[8]流程:
(1) 输入给定信号s(t),确定极值点阶数n。
(2) 分别确定n阶极大值点un(tk),极小值点ln(tk),极小极大值点lun(tk),极大极小值点uln(tk)。
(3) 分别通过三次样条插值构造上包络线un(t)、下包络线ln(t)。以及极小上包络线lun(t)、极大下包络线uln(t)。
(4) 计算出三个不同的包络均值m1(t)=(un(t)+ln(t))/2、m2(t)=(uln(t)+lun(t))/2、m3(t)=(un(t)+ln(t)+uln(t)+lun(t))/4判断包络均值是否满足给定条件OC,满足的话,从三个均值中选择最优均值执行步聚(5),否则,跳转至步骤(6)。
(5) 让c1(t)+c1(t)+m(t)和s(t)=s(t)-m(t)重复以上操作直到m(t)不再满足给定条件。这时剩余信号是最高频率IMF1。
(6) 让n=n-1,重复步骤(1)~(5),直至n=1,得到剩余信号r(t)即为最高频IMF1。
(7) 让s(t)=s(t)-r(t),重复步骤(1)~(6),得到其他的IMF,直至所有IMF之和满足给定条件OC1,则EMD循环终止,得到一个非本征模态函数的残余信号。
3 逆EMD存在的问题以及改进的方法
逆EMD与标准EMD方法的最大不同之处在于最优包络均值的拟合过程。通常,最优包络均值是复杂的多分量、非平稳信号。标准EMD方法通过多次三次样条插值来拟合,而逆EMD方法考虑到信号多分量的特点,采用不同阶极值点来拟合该最优包络均值。该方法的优势是:可以有效的减小估计误差,同时有效的抑制多余IMF分量。但是逆EMD方法中,由于不同阶极值点是根据多分量信号特点提出的,所以不适用于复杂实际信号尤其是信号分量频率差别较低的情况。逆EMD方法采用n阶包络深入式的逆向筛选,过分依赖不同阶极值点拟合最优包络均值,导致低阶包络均值筛分的强度不够,从而得到的高频分量误差较大。所以本文提出了一种二阶包络逆向筛分与多次使用三次样条插值拟合相结合的逆EMD改进方法。既保证了对信号分解时有效的估计,同时不会因高阶极值点问题局限逆EMD仅适用于分解一些高频率差的多分量信号,同时减小了高频分量误差。
一个IMF必须满足以下两个条件[9]:①在整个数据长度,极值和过零点的数目必须相等或最多相差一个;②在任意数据点,局部最大值的包络和局部最小值的包络的平均必须为0。在逆EMD分解过程中发现,当筛选进行一定程度时,其分解的信号已经满足本征模态函数的基本条件,但由于上、下拟合的包络有错差问题致使其上、下包络不对称,导致筛选过程不能很快的收敛并且结束。这样的情况如图1所示,该测试信号完全满足本征模态函数条件,其过零点次数与极值点个数相差为零,可是由于原始信号极小值点位置情况,导致将下包络错误的拟合成了一条近似直线,使得包络均值不能为零,如图1的浅灰色曲线(原始的上、下包络线)所示。所以为了避免类似的情况发生,我们采用将极大值点翻转变为极小值点与信号极小值点一起拟合成下包络,如图1的深灰色曲线(新的下包络线)所示。这样它们的包络均值为零。图1中浅灰色曲线为原始包络线,深灰色为修正后包络线。
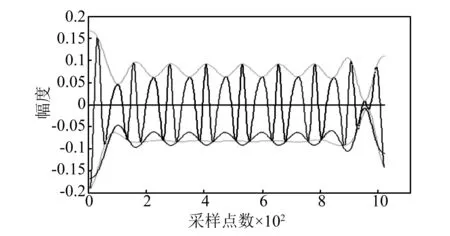
图1 测试信号Fig.1 Test signal
为了避免类似情况的发生,在逆EMD算法中做了如下改进:将极大值点翻转作为信号的极小值点来重新拟合新的下包络,同样方法将极小值点翻转作为信号的极大值点来重新拟合成新的上包络。然后通过条件判断哪种上下包络更符合要求(即包络均值更接近零均值)而考虑选择哪种包络。该方法通过改变包络拟合方式,从而改变了包络均值,而IMF的正交性停止准则主要受包络均值m(t)与输入信号s(t)的相关性(m(t)=b·s(t),b为相关系数)所影响,所以筛选过程中,采用该方法包络均值快速收敛接近零均值,m(t)与s(t)相关性减小,同时正交性OC逼近停止条件,进而不致于过分的筛分出无物理意义的其他分量。由于整个筛分过程采用的是由OC选择最优包络均值的方式,选择使得OC最大的m(t)作为最优包络,也就是在筛分时筛分掉的是与信号s(t)相关性最大的包络均值,所以一定程度上保证了分解得到IMF分量的正交性。
4 逆EMD的改进算法
改进逆EMD的算法流程如下:
(1) 设置初始值n=1,输入给定信号s(t)。
(2) 分别确定信号极大值点U(t),信号极小值点L(t),将极小值点翻折构成新的极大值点集U1(t),将极大值点翻折构成新的极小值点集L1(t),利用三次样条插值构造原始(上下)包络以及翻折后的(上下)包络,通过条件判断原始包络和翻折包络来选择作为一阶包络m1(t)。
(3) 分别确定信号中极小的极大值点LU(t),极大的极小值点UL(t),利用三次样条插值构造上、下包络,获得二阶包络m2(t)。
(4) 分别获得三种包络均值:一阶包络均值m1(t)、二阶包络均值m2(t)、一阶包络与二阶包络的平均值:m3(t)=(m1(t)+m2(t))/2,判断三种包络均值是否满足给定条件OC>1.05,满足的话,从三种包络均值中选择最优均值(也就是从三种包络均值中选择使得OC最大的m(t)作为最优均值)执行步骤(5),否则,跳转至步骤(6)。
(5) 让c1(t)=c1(t)+m(t) 和s(t)=s(t)-m(t)重复以上操作直到m(t)不再满足给定条件。这时剩余信号是最高频率IMF1。
(6) 让n=n+1,s(t)=s(t)-IMF(t),重复步骤(1)~(5),得到其他的IMF,直至所有IMF之和满足给定条件OC1,则EMD循环终止,得到一个非本征模态函数的残余信号。
信号经逆EMD分解后可用如下式子表达:
S(t)=IMF1+IMF2+IMFn+rn(t)
(2)
n表示EMD分解所得的IMF个数。
改进前逆EMD分解效果如图2、3所示;改进后逆EMD分解效果如图4、5所示。
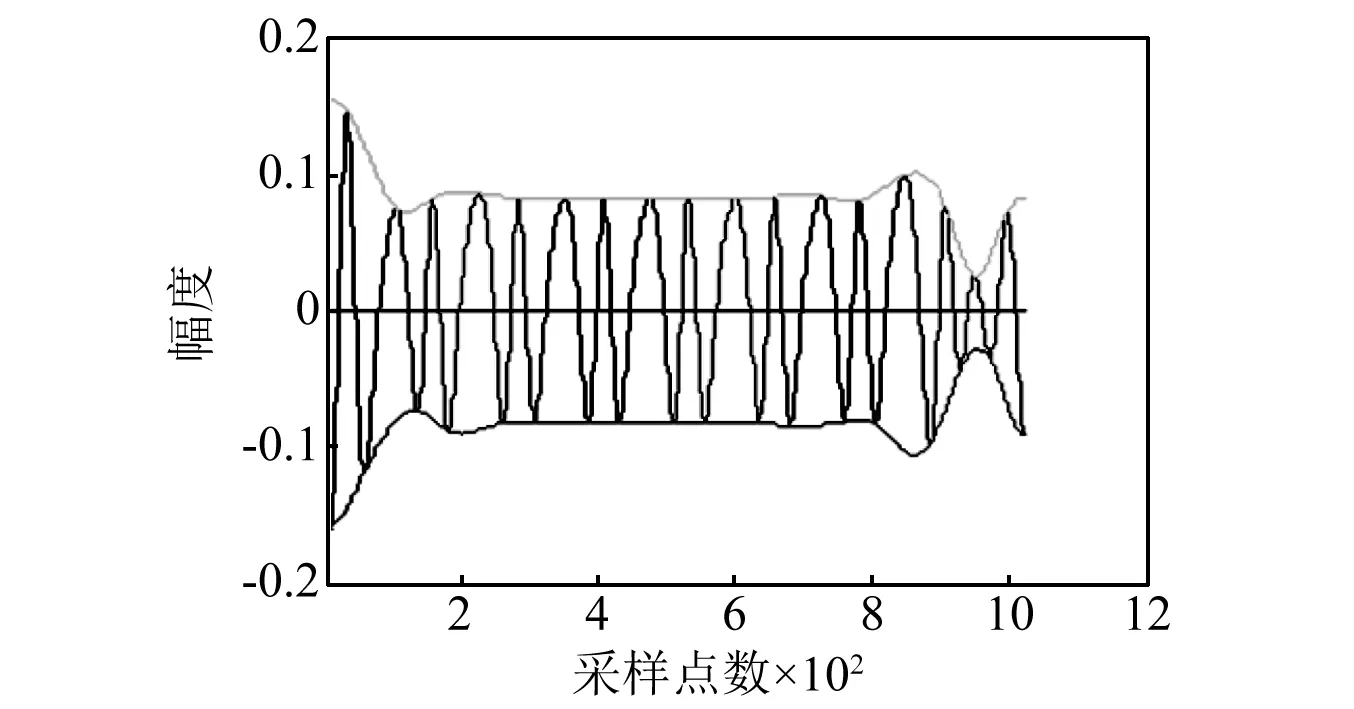
图2 改进前逆EMD分解所得IMF1Fig.2 IMF1 of inverse EMD
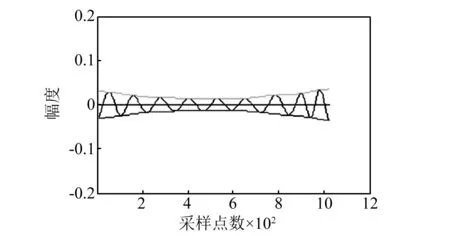
图3 改进前逆EMD分解所得IMF2Fig.3 IMF2 of inverse EMD
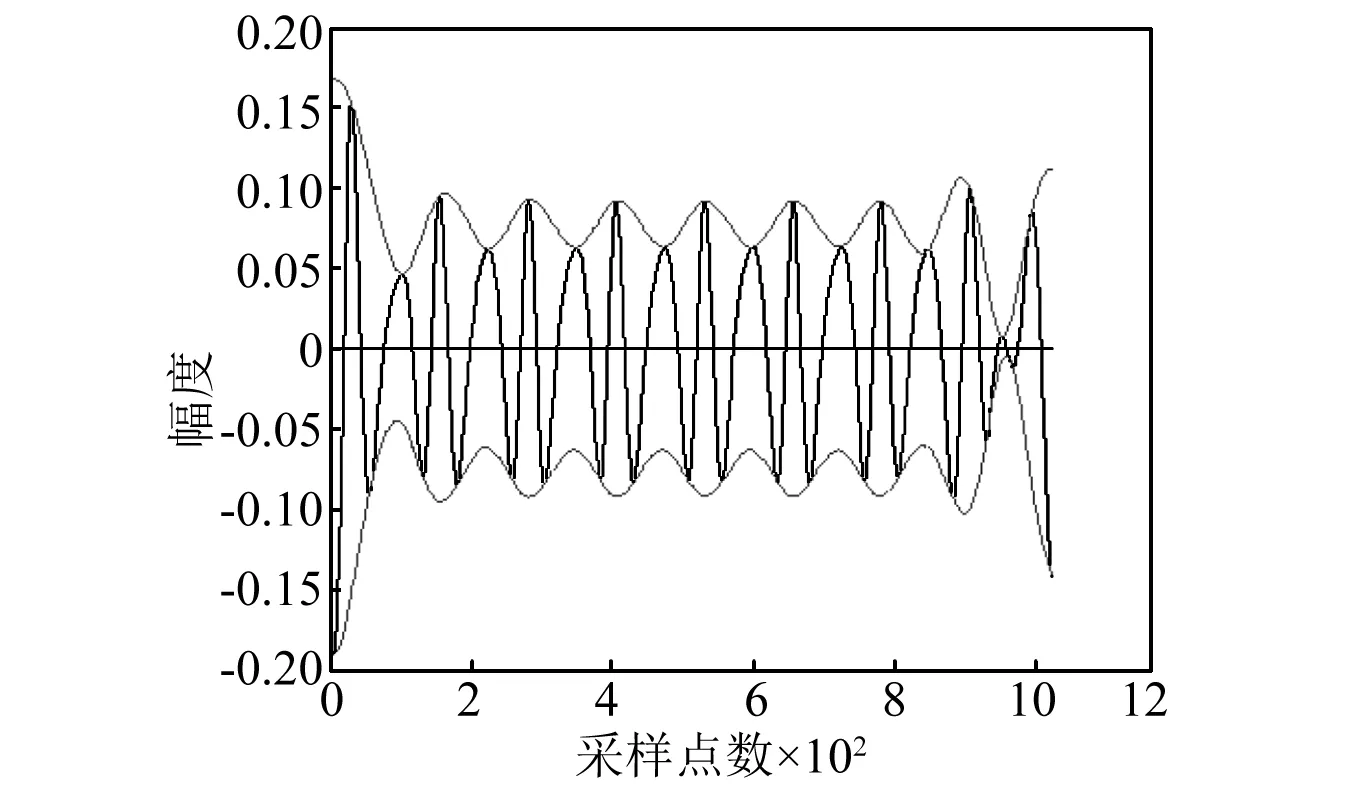
图4 改进后逆EMD分解所得IMF1Fig.4 IMF1 of improved inverse EMD

图5 改进后逆EMD分解所得IMF2Fig.5 IMF2 of improved inverse EMD
根据本征模态函数定义,其实上述测试信号已经满足本征模态函数条件。可是当用改进前逆EMD算法来进行分解时,会得到两个信号成分IMF1和IMF2,通过图2、3与图4、5比较可知,原逆EMD比改进后逆EMD筛分的程度更强,IMF信号的带宽更窄。这表明,在原逆EMD的筛选过程,容易导致过分筛选现象。也就是在本来满足条件的本征模态函数信号中,如果继续不断的筛选,从主幅度的IMF信号中会筛分出一个小幅度的IMF信号,即过分的筛分出无物理意义的其他分量。而当经改进后逆EMD算法分解时,其几乎是不能再次分解的,且其得到的IMF2分量几乎不含任何信号成分,信号幅度一直在零值附近。如图4、5所示。由于包络没有严格的数学定义,采用这样的一种方式构造新包络,虽然一定程度上增加了IMF的带宽,但可以有效的避免EMD分解过程中的IMF过筛选现象,可以保证IMF的信号完整性,而不会过分的筛分出其他分量。
实验1 正交性测试
为了验证本文方法的有效性,本次测试采用式(1)的正交性( Index of Orthogonality, IO) 指标来比较经典EMD和逆EMD分解的性能。
(3)
IO指标越接近于0,说明EMD分解得到的各个内蕴模式函数之间越接近于正交。
基于P.Flandrin数值实验结论[10]:
当两信号频率比a<0.5(a=f2/f1,f2
我们构造信号针对于完全分离、部分分离、完全不能分离三种情况,分别测试正交性指标来比较经典EMD与逆EMD分解的性能。
构造完全分离时的仿真信号:
y1=cos((α·f0(i))·2·pi·t)
y2=cos((β·f0(i))·2·pi·t)
t∈(1,1 024)
y=y1+y2
其中f0在频率0至0.5范围内,频域等距的500个仿真信号,完全分离时设置α=1,β=0.4;部分分离时设置α=1,β=0.6;完全不能分离时设置α=1,β=0.7。
从图6~图8可以看出,当两种信号成分无论是完全分离、部分分离、还是完全不能分离,通过逆EMD分解方法得到两成分IMF1和IMF2,其正交性都比标准EMD效果要好。而且随着频率差值的逐渐接近,二阶包络逆EMD体现出更好的分解效果。换言之,该方法比经典EMD、逆EMD更适用于分解一些频率差值较低的多分量信号。
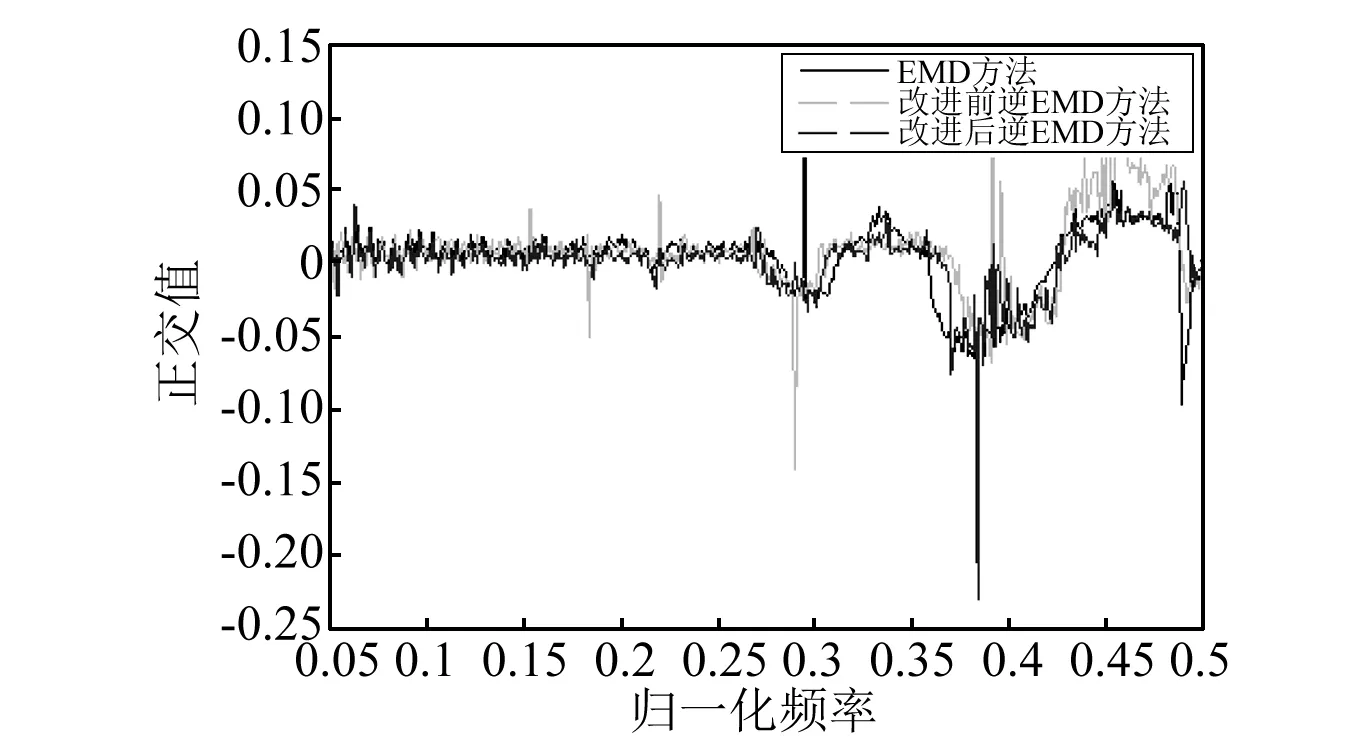
图6 完全分离Fig.6 Completely separate
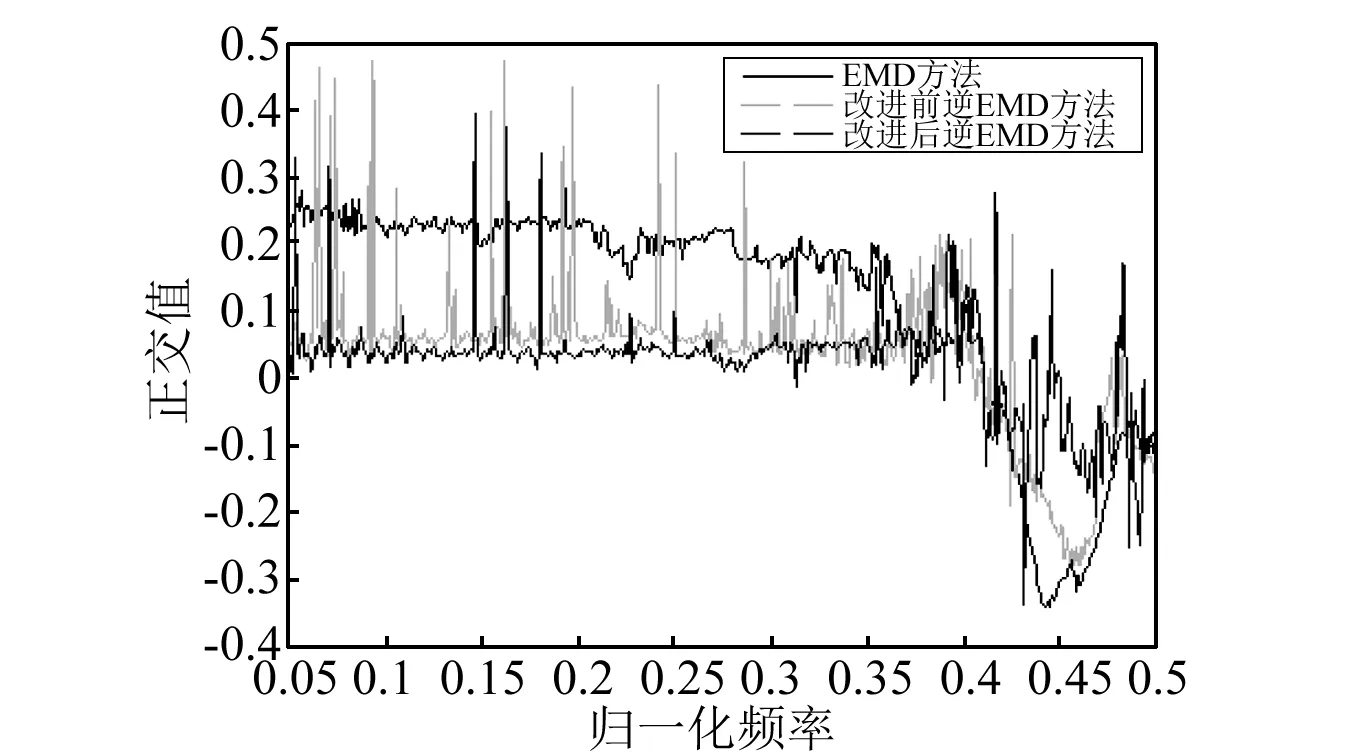
图7 部分分离Fig.7 Partly separate

图8 完全不能分离Fig.8 Completely unable to separate
实验2 能量泄漏测试
在EMD算法中,每个IMF分量都是经过多次筛选的过程来获得,而每次筛选的过程都是通过信号的局部极大、极小值点用三次样条插值的方法拟合而成的上、下包络线的均值。但是由于采样间隔的存在,信号的局部极值点很有可能定位失配,从而会产生极值点定位的偏离误差,最终影响会体现在EMD分解中,我们称之为能量泄漏。在理想的情况下,如果原始信号是单频率的正余弦信号,对其进行EMD分解,由于信号的上下包络线是完全对称的,所以分解的结果就只会有一个IMF分量即为此正余弦信号。而实际上,将信号进行EMD分解时,由于采样频率的缘故,离散的单频率信号其上下包络线并不能完全的对称,最终导致会有多个IMF的结果,我们就说,采样引起的非对准使得EMD分解的部分能量泄漏到其他的IMF中了。
对不同采样频率的单位幅度单频率正弦信号进行EMD分解,定义由于采样的非对准而造成其能量泄漏公式为:
(4)
式中N为数据段长度,r为EMD分解的层数,求和到r+1意味着包括余量。End_error指标越接近于0,说明EMD分解越接近无损。
测试信号:
y=cos((1.0·f0(i)·2·pi·t)
t∈(1,1 024)
其中f0在频域0至0.5范围内,频率等距选择500个频率点用来构造仿真信号。

图9 EMD分解与逆EMD分解能量泄漏的比较Fig.9 Energy leakage contrast of EMD and inverse EMD
由图9可知三种EMD方法的能量泄漏均满足非对准误差曲线。从整个频域角度来看,在一些频率点位置,逆EMD分解的能量泄漏明显低于标准的EMD分解能量泄漏值。当用SUM_EMD来求三种方法在全频段的能量泄漏占用总面积时,逆EMD能量泄漏总值小于标准EMD,即在全频段,逆EMD效果更好。改进前、后逆EMD方法的能量泄漏曲线很接近,但是改进后的逆EMD能量泄漏普遍小于改进前逆EMD。通过对三种EMD方法能量泄漏测试,实验证明,改进的逆EMD方法效果最好。
前面进行了三种EMD方法正交性以及能量泄漏的测试与比较,下面探讨在逆EMD分解过程中分别采用三种包络曲线去实现信号的筛选,并测试其分解后的能量泄漏。第一种:在逆EMD分解过程中,整个过程使用的是一阶包络曲线求取包络均值(m1)去完成信号的筛选;第二种:整个过程采用的是一阶与二阶包络曲线共同求取包络均值(m3)去完成信号的筛选;第三种:整个过程将一阶包络均值、二阶包络均值以及一阶与二阶两个包络的平均值通过一个准则从中选择一个作为最优包络均值(option)去完成信号的筛选。
实验3 针对这三种方式,测试其在逆EMD分解过程中能量泄漏指标

图10 三种包络方式的能量泄漏Fig.10 Energy leakage of three kinds of envelope
图10中深灰色为最优包络方法,浅灰色为一阶包络方法,处于深灰色与浅灰色曲线之间的曲线为二阶包络方法。这三种包络曲线方法在逆EMD分解过程中的能量泄漏均满足非对准误差曲线。三种方法的能量泄漏值比较接近,但是最优包络在逆EMD中效果更佳。
实验4 改进的逆EMD在信号处理中的应用
心电图信号是一种微弱的生物电信号,也是一种典型的非平稳随机信号。该方法可以有效地减小高频分量误差,抑制多余IMF分量等诸多优势。在此,将改进后的逆EMD方法应用到心电图信号的分解中,并把处理结果同改进前的EMD分解方法作比较,以对比处理效果。
本次测试采用的心电图信号来源于近年来应用比较广泛的国际上公认的美国麻省理工学院提供的MIT-BIH数据库。图11和图12中最上面的信号s(t)为一段心电图信号,含有高频噪声干扰和电平整体偏置;最下面的信号res.为剩余信号,主要为整体偏置电平;c1(t)含有较多的高频噪声;c2(t)主要包含了心电信号。 改进后EMD得到的c2(t)与改进前EMD的相比高频噪声幅度明显较小,可以忽略不计,说明改进后EMD方法可以有效地减小高频分量误差。改进前分解得6个IMF分量,改进后分解得4个IMF分量,说明改进后EMD方法可以有效抑制多余IMF分量。

图11 改进前逆EMD分解结果Fig.11 Result of inverse EMD
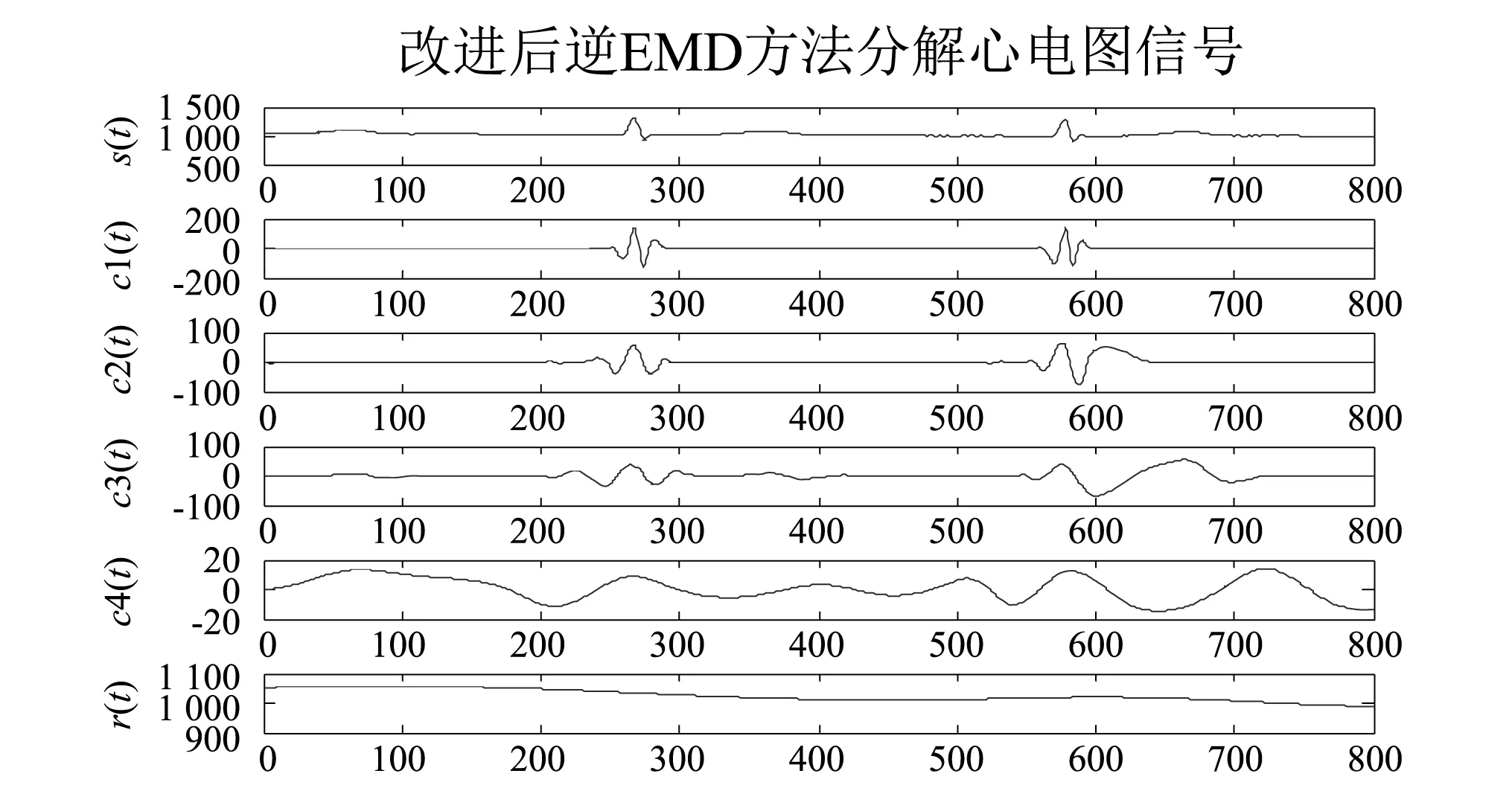
图12 改进后逆EMD分解结果Fig.12 Result of improved inverse EMD
4 结 论
本文提出基于二阶包络逆向筛分的EMD方法,该方法有效的结合经典EMD与高阶逆EMD的优势。数值实验证明该方法不仅适用于多分量信号,而且适用于复杂实际信号。对于分解一些频率差值较低的多分量信号,可以减小高频分量误差。可以有效的减小估计误差,抑制多余IMF分量。
[ 1 ] HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-s tationary time series analysis[J]. Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences. The Royal Society, 1998, 454(1971):
903-995.
[ 2 ] 徐冠雷, 王孝通, 徐晓刚, 等. 多分量到单分量可用 EMD 分解的条件及判据[J]. 自然科学进展, 2006, 16(10): 1356-1360. XU Guanlei, WANG Xiaotong, XU Xiaogang, et al. Conditions and criteria of EMD for multi-component to single component [J]. Progress in Natural Science, 2006, 16(10): 1356-1360.
[ 3 ] KOPSINIS Y, MCLAUGHLIN S. Enhanced empirical mode decomposition using a novel sifting-based interpolation points detection[C]. IEEE/SP Workshop on Statistical Signal Processing, 2007,53(3): 315-318.
[ 4 ] KOPSINIS Y, MCLAUGHLIN S. Investigation and performance enhancement of the empirical mode decomposition method based on a heuristic search optimization approach[J]. Signal Processing, IEEE Transactions on, 2008, 56(1): 1-13.
[ 5 ] XU Guanlei, WANG Xiaotong, XU Xiaogang. Neighborhood limited empirical mode decomposition and application in image processing[C]∥ Proceeding of the fourth International Conference on Image and Graphics. Washingdon, DC:ICIG, 2007.
[ 6 ] LI Lin, JI Hongbing. Signal feature extraction based on an improved EMD method[J]. Measurement, 2009, 42(5): 796-803.
[ 7 ] HUANG N E, SHEN Z, LONG S R. A new view of nonlinear water waves: The Hilbert Spectrum 1[J]. Annual review of fluid mechanics, 1999, 31(1): 417-457.
[ 8 ] 江莉, 李林, 董惠. 基于改进 EMD 方法的多分量信号分析[J]. 振动与冲击, 2009, 28(4): 51-53. JIANG Li, LI Lin, DONG Hui. An improved empirical mode decomposition method for multicomponent signal represntation [J]. Journal of Vibration and Shock, 2009, 28(4): 51-53.
[ 9 ] 郑天翔, 杨力华. 经验模式分解算法的探讨和改进[J]. 中山大学学报 (自然科学版), 2007, 46(1): 1-6. ZHENG Tianxiang, YANG Lihua. Discussion and improvement on empirical mode decomposition algorithm[J]. Journal of Zhongshan University (Natural Science Edition) , 2007, 46(1): 1-6.
[10] RILLING G, FLANDRIN P. One or two frequencies?The empirical mode decomposition answers[J]. Signal Processing, IEEE Transactions on, 2008, 56(1): 85-95.
Improvement and implementation of inverse EMD algorithm based on second order envelope
HE Jingwei, HU Weiping, MO Jialing
(Guangxi Key Lab of Multi-source Information Ming & Security, College of Electronic Engineering, Guangxi Normal University, Guilin 541004,China)
On the basis of analysing the classic empirical mode decomposition (EMD) method and the inverse EMD method in which the high-order extreme value point is used in reverse screening, a method based on second order envelope inverse EMD was proposed. The method integrates the good properties of the classic EMD and inverse EMD. Making use of the first and second order envelope and introducing certain conditions in the screening process, the mean value of an optimal envelope was chosen for screening.The experimental results show that the method is suitable for being applied to decompose multi-component signals with low frequency difference between components. It can reduce the error of high frequency components, effectively decrease the estimation error and restrain the excess IMF components.The EMD decomposition effect will be better when the optimal envelope is adopted in screening.
classic EMD; inverse EMD; inverse EMD based on second order envelope
国家自然科学基金资助项目(61062011;61362003);广西多源信息挖掘与安全重点实验室基金项目(13-A-03-02);广西壮族自治区高等学校科学研究项目(KY2015YB034)
2015-07-14 修改稿收到日期: 2016-01-21
何经伟 男,硕士,1988年生
胡维平 男,博士,教授,1963年生
TN911.7
A
10.13465/j.cnki.jvs.2017.07.019
