转炉用扭力杆系统振动理论研究
2017-04-11吴林峰
吴林峰,王 文
(华北水利水电大学 机械学院,郑州 450008)
转炉用扭力杆系统振动理论研究
吴林峰,王 文
(华北水利水电大学 机械学院,郑州 450008)
扭力杆系统的动态特性对转炉设备工作的可靠性有着重要影响,研究其振动频率和阵型是设备自主创新的关键技术之一。综合考虑扭力杆系统实际结构组成,提出了均质杆和集中质量杆一端铰支另一端简支反对称弯曲振动梁、均质杆和集中质量杆一端固支另一端简支反对称弯曲振动梁等四种振动模型。以某厂150 t氧气顶吹转炉扭力杆系统为例进行了理论计算。结果表明,扭力杆系统振动模型采用集中质量杆一端固支和一端简支反对称弯曲振动梁模型更合理。并用有限元法对其正确性进行了验证,两种方法的计算结果吻合,都可以对扭力杆系统进行研究,但是理论解更为简单方便,便于工程技术人员直接引用,为指导工程实际设计和生产提供了理论基础。
转炉;扭力杆系统;振动梁模型;理论解;有限元解
扭力杆能够利用自身的弹性扭转变形储备能量、传递扭矩、协调输出力矩平衡及在柔性支撑中取代体积较大的轴承等功能,在大小型设备上都得到了广泛的应用[1]。对于扭力杆(系统)的研究,有数值法[2-3]、实验测试法[4]、刚度精度求解法[5-6]以及利用摄动法进行可靠性设计[7]等方法。以上研究都是对扭力杆系统进行的静态研究。
大型转炉用扭力杆用于储存现代转炉快速摇炉倾动过程的冲击振动,是减缓快速摇炉对传动系统的冲击,避免泼钢等恶性事故发生,保障生产安全的重要组成部分。扭力杆系统的静态研究不能完全满足生产需要,而对扭力杆(系统)的动态特性研究只有郑龙捷[8]对大吨位用扭力杆异常振动进行了研究。
我国对于大型转炉设备建设,目前依靠引进国外设计技术,利用国内制作和安装技术进行建造[9]。同时设备引进时,加之国外对相关技术的保密,没有任何产品相关的核心技术,国内对大型转炉的设计技术和使用技术一直处于探索阶段,严重束缚了转炉炼钢设备的自主创新与开发。因此,对扭力杆系统进行动态理论研究,具有重要的理论指导和工程应用价值。
本文综合考虑转炉用扭力杆系统可能存在的振动模型,提出新的扭振理论设计方法,并进行三维全尺寸有限元数值计算,对理论方法的可行性进行验证。
1 扭力杆系统振动模型建立
扭力杆位于减速机箱体下方,安装在两端支承轴承座上。炉体制动时,由于炉体与减速机整体绕耳轴转动,减速机下部左右两传力曲柄,一个受拉,一个受压,将倾动机构传来的力矩传递给扭力杆,在曲柄两端形成大小相等、方向相反的一对力偶,使扭力杆发生扭转变形从而起到支撑与缓冲作用[10]。对于呈现空间布置的扭力杆而言,其振动模态复杂,包括扭转模态,纵向弯曲模态,横向弯曲模态等。实际工作中,与扭力杆系统工作特性最相关的是倾动自振模态,就是扭力杆曲柄对扭力杆轴线的反对称的弯曲模态。因此,研究扭力杆对自振模态的倾动自振频率成为研究的关键。
对扭力杆系统建立如图1所示的坐标系,规定扭力杆轴为x轴,其中有轴向窜动的一端为正向,有轴向定位一端的支承轴承对称中心线与x轴的交点为原点(记为点1),两个传力曲柄对称中心线与扭力杆轴线交点记为2和3,有轴向窜动的支承轴承对称中心线与扭力杆轴线的交点记为点4。
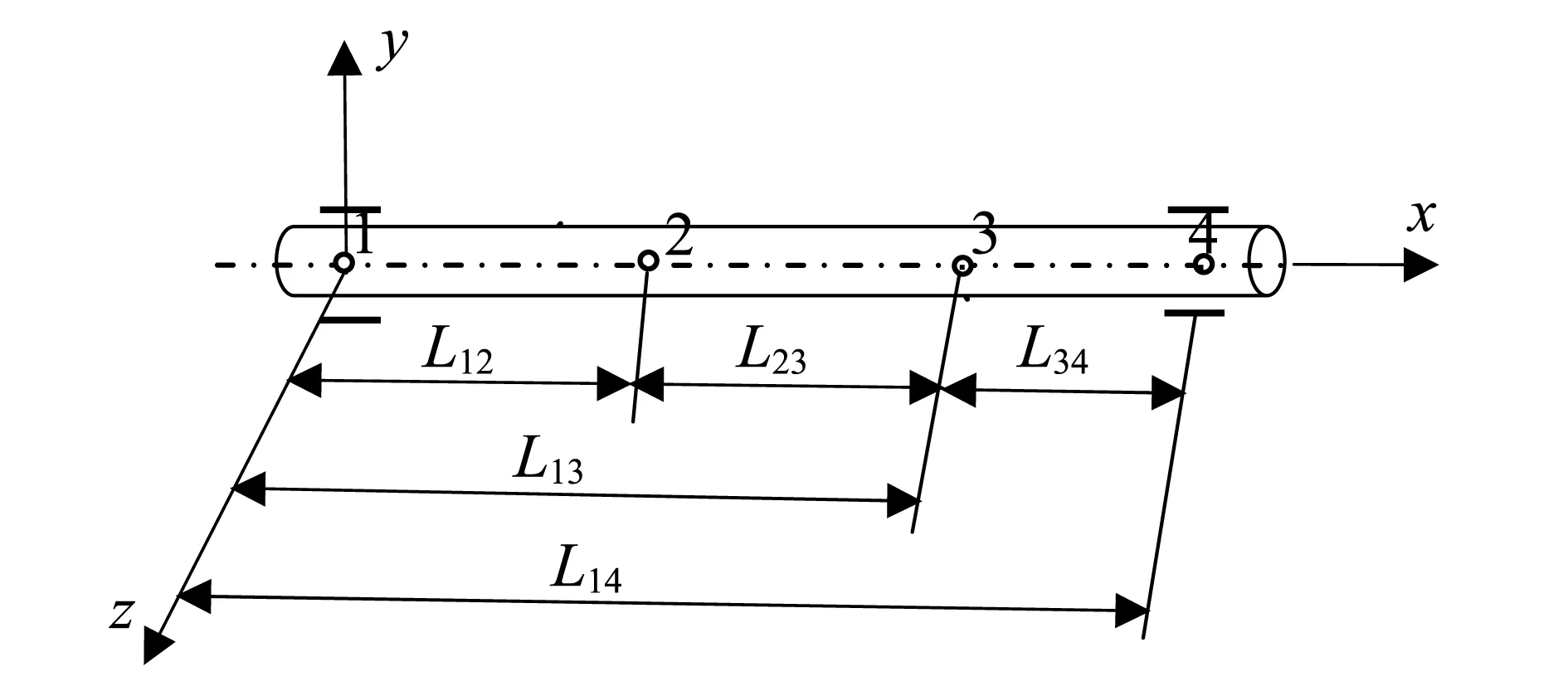
1、4-支承轴承对称中心线与扭力杆轴线交点;2、3-传力曲柄对称中心线与扭力杆轴线交点;L12-点1和2的距离;L23-点2和3的距离;L34-点3和4的距离; L13-点1和3的距离;L14-点1和4的距离图1 扭力杆系统坐标系Fig.1 Torsion bar system coordinates
1.1 均质杆一端铰支、一端简支反对称弯曲振动模型——模型一
如果仅考虑扭力杆质量,不考虑传力曲柄、传力块和卡盘质量,将扭力杆等效为一等直圆杆(如图2所示),有轴向定位的一端简化为铰支端、允许有轴向窜动的一端简化为简支端,则该振动模态对应简支梁振动的二阶模态。根据振动理论的研究结果[11-13],该均质杆一端铰支、一端简支反对称弯曲振动模型模态圆频率为
(1)
式中,E为弹性模量,Iz为扭力杆对z轴的转动惯量,ρ为材料密度,A为扭力杆截面积。
归一化后的模态振幅为
(2)

图2 均质杆一端铰支一端简支梁模型Fig.2 Homogeneous bar which is hinged at one end and simply supported at the other
1.2 集中质量杆一端铰支、一端简支反对称弯曲振动模型——模型二
如果考虑传力曲柄、传力块和卡盘质量,将扭力杆的质量分两部分考虑,分别和卡盘、曲柄质量看作两个集中质量块(作用在曲柄对称中心线与扭力杆轴线交点2和点3处)。建立一端铰支一端简支梁模型(如图3所示),利用集中质量法和瑞利法进行求解。

m0-扭力杆一半质量、曲柄和卡盘质量之和图3 集中质量杆一端铰支一端简支梁模型Fig.3 Concentrated mass bar which is hinged at one end and simply supported at the other
设模态函数为
(3)
则根据振动动能等于振动变形的关系得到振动圆频率为
进一步求解得到圆频率为
(4)
模型二模态振幅同式(2)。
1.3 均质杆一端固支、一端简支反对称弯曲振动模型——模型三
由于轴承有一定的宽度,其实际对扭力杆的支承,还不完全等同于铰支。为此,将扭力杆有轴向定位的一端简化为固支端,允许轴向窜动的一端简化为简支端(不考虑传力曲柄、传力块和卡盘质量),模型如图4所示。
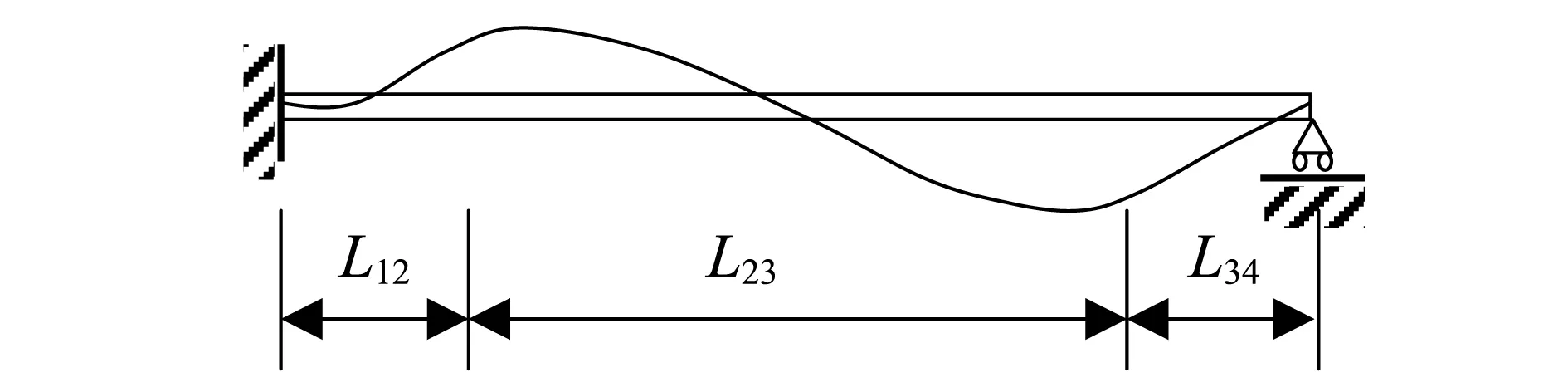
图4 均质杆一端固支、一端简支振动模型Fig.4 Homogeneous bar which is clamped hinged at one end and simply supported at the other end
根据模型计算得到的二阶模态的圆频率公式为
(5)
式中,β=2.25π。
振幅为
(6)
1.4 集中质量杆一端固支、一端简支反对称弯曲振动模型——模型四
考虑传力曲柄、传力块和卡盘质量,利用集中质量法,所建立的模型如图5所示(有轴向定位的一端简化为固支端、允许有轴向窜动的一端简化为简支端)。
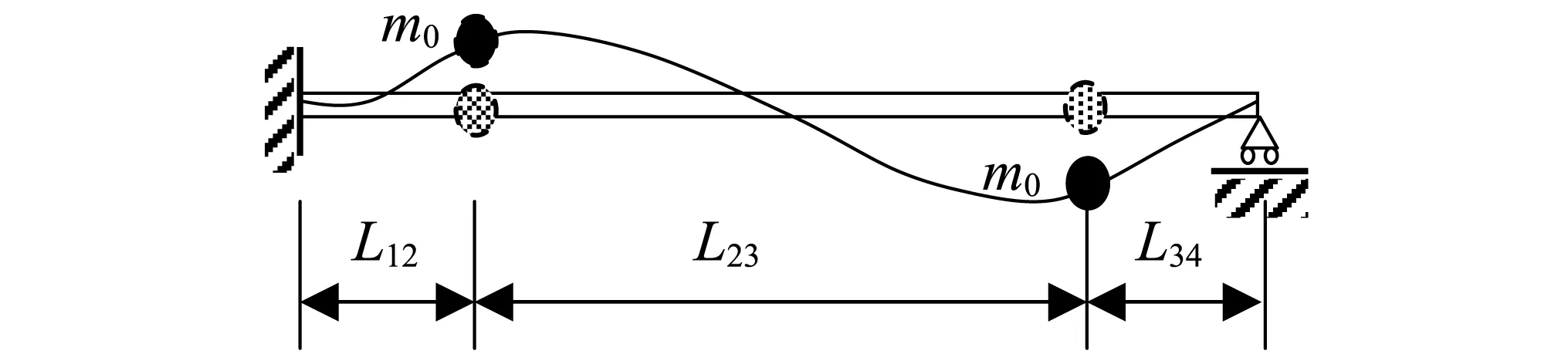
图5 集中质量杆一端固支、一端简支振动模型Fig.5 Vibration model of concentrated mass bar which is clamped hinged at one end and simply supported at the other end
选取模态函数为
(7)

则根据振动动能等于振动变形的关系得到圆频率为
(8)
2 质量对振动频率的影响
由式(1)、式(2)、式(4)、式(5)、式(6)和式(8)可推知不同模型扭力杆系统的圆频率和振幅大小,再由频率和圆频率的关系求出频率的大小。以某厂设计的150 t氧气顶吹转炉扭力杆系统设计参数为例(如表1所示)进行计算,得到扭力杆系统的圆频率和固有频率以及振幅大小(如表2所示)。

表1 扭力杆结构参数Tab. 1 Structural parameters of torsion bar
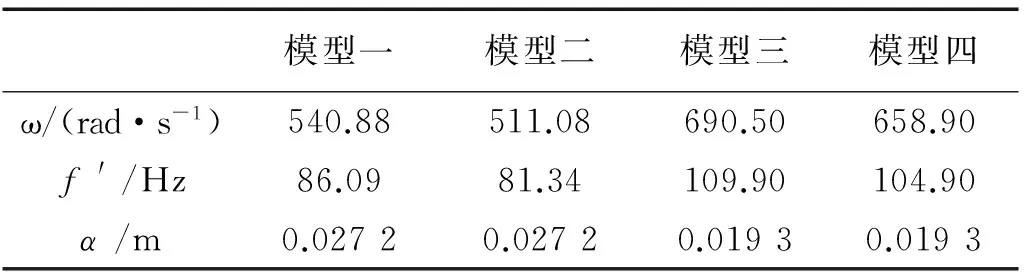
表2 理论计算结果Tab. 2 The theoretical results
从表2计算结果可知:模型一和模型二两者的圆频率相差29.80 rad/s,频率相差4.75 Hz,两者振幅相等,这说明曲柄、传力块和卡盘质量对一端固铰支、一端简支梁模型振动影响差别不是很大;模型三和模型四两者的圆频率相差31.60 rad/s,频率相差5.00 Hz,这说明曲柄、传力块和卡盘质量对一端固支、一端简支反对称弯曲振动模型影响差别也不是很大。但是,质量对梁不同支承端方式影响很大,比如模型一二和模型三、四相比,圆频率、频率和振幅分别最大相差179.41 rad/s、28.56 Hz和7.9 mm,这说明质量对扭力杆系统频率和振幅的影响不能忽略,结合扭力杆系统结构的实际情况:扭力杆系统,以扭力杆为主体,主体上有用来传递扭矩的曲柄、卡盘和传力块、在两端有支承轴承(一端用来轴向定位,一端有轴向窜动),这些结构相对于扭力杆系统来说,质量影响不容忽视,模型分析中不能忽略。因此扭力杆模型研究考虑真实情况结果是:即选择集中质量杆模型,同时扭力杆本体实际上是一端轴向固定、另一端是可以轴向窜动的模型比较接近实际,因此,选择模型四分析扭力杆系统更为准确和合理。
3 有限元计算结果分析
图2~图5所示的模型理论计算时作了一定简化,例如,扭力杆本体轴向尺寸是变截面的、曲柄和卡盘长度非定尺寸,而理论分析计算是看作固定尺寸分析的,轴承有一定的宽度而理论分析中没有考虑,这些与扭力杆系统结构的真实尺寸还存在一定的差别,有必要用较为真实的三维结构模型和接触传力方式进行有限元计算,分析相应的简化对计算结果造成的影响。
为了验证理论公式的合理性,考虑实际工况的接触传力方式,对扭力杆系统进行了三维全尺寸结构模型有限元方法数值计算。数值模拟扭力杆振动特性,通过对比分析,验证理论设计方法的可靠性和精度。
在模型中,充分考虑扭力杆两端轴颈与轴承座的轴瓦接触、传力曲柄梅花轴头与扭力杆端部的接触,选用柔体-柔体的面-面接触形式,选用非线性算法[14]进行接触计算。
表3为有限元方法计算得到的扭力杆五阶自振频率,图6为扭力杆系统第一阶振动模态。结果显示,一阶模态是竖向反对称弯曲模态,二阶模态为水平反对称弯曲模态,三阶模态为水平对称弯曲模态,四阶模态为竖向对称弯曲模态,五阶模态为扭转模态。

表3 扭力杆前五阶自振频率和相应的模态振幅Tab. 3 The first 5-order nature frequencies and its corresponding modal amplitudes
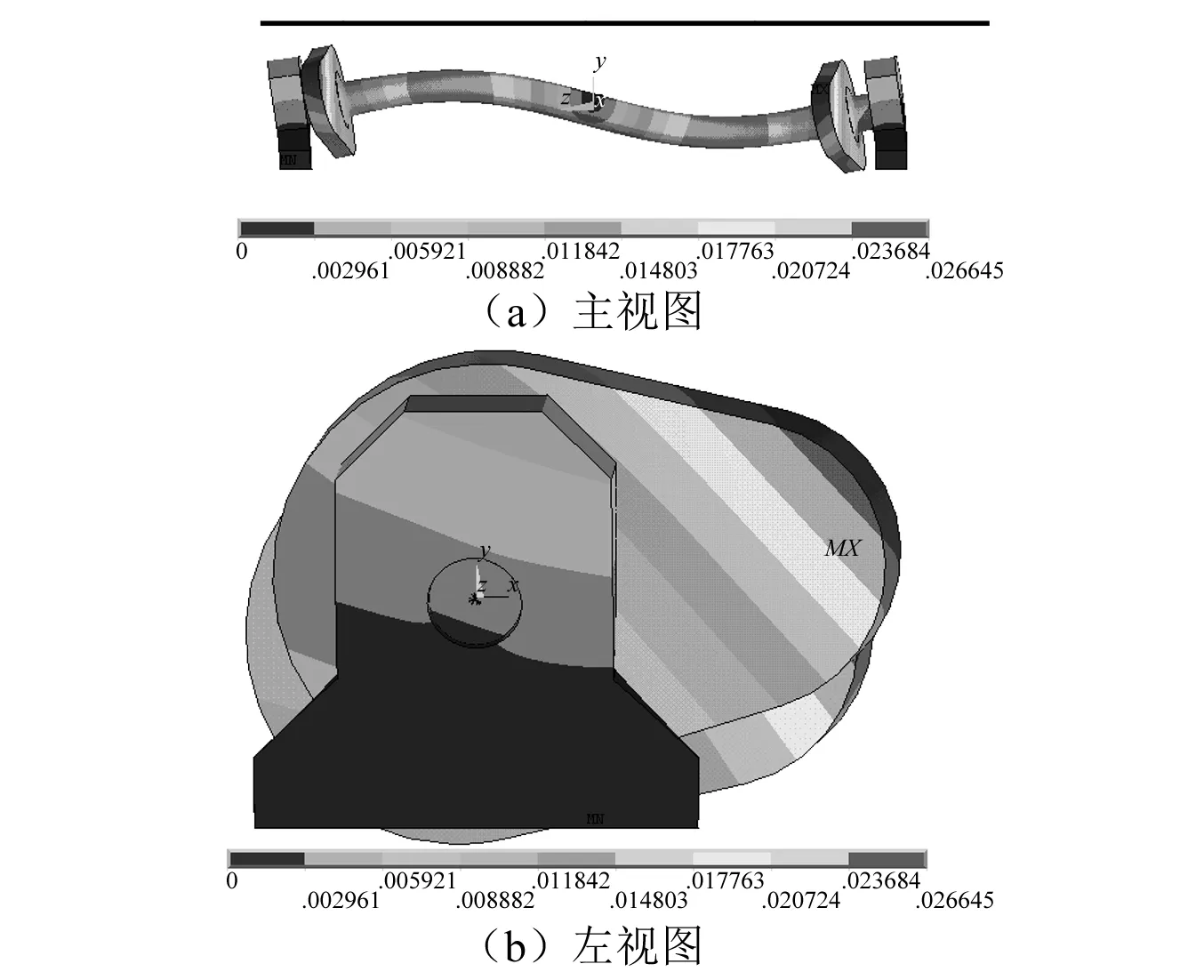
图6 扭力杆系统第一阶阵型Fig.6 The first order formation of torsion bar system
考虑传力曲柄、传力块和卡盘质量的集中质量的一端固支、一端简支的梁模型理论计算(模型四)的一阶频率104.9 Hz,与有限元方法计算的一阶频率107.70 Hz值相差 仅2.6%。模型四计算得到的模态振幅为0.019 25 m,有限元计算一阶振幅为0.027 m,两者相差28.7%。理论解比有限元解小,其原因是理论计算值只考虑了曲柄、传力块、卡盘的质量,没有考虑其相应的几何尺寸,有限元解将两者都考虑了,所以理论解的模态幅值是指扭力杆上的值,而有限元解的模态幅值是指曲柄端部的幅值。以上误差属于工程设计使用的误差范围之内,理论模型四相应的频率、振幅计算公式可以用来支持实际工程设计应用,尤其是振动频率的理论公式,对研究扭力杆系统振动特性的通用性研究具有重要的指导意义。
该部分设计,结合转炉其他结构部分的设计,开发的150 t国产化新转炉,转炉自2007年正式投入生产以来,摇炉速度为1.60 r/mim,整个设备工作正常。该扭力杆系统的固有频率远远高于转炉设备的工作频率,避开了发生共振的可能,可用以指导炼钢生产实际。
4 结 论
本文综合考虑了扭力杆系统可能存在的四种模型并推导出四种模型的圆频率和振幅理论公式。并以150 t转炉扭力杆系统对四种模型进行讨论,得出扭力杆系统集中质量杆一端固支、一端简支梁模型更符合实际。又用有限元法对该模型理论解进行了对比,得出以下结论:
(1)集中质量杆一端固支、一端简支梁模型(模型四)更符合扭力杆系统振动研究。
(2)模型四的振动频率和振幅理论公式在同类扭力杆系统设计时,只需要将扭力杆系统的结构尺寸代入,可以直接引用公式计算。
(3)由于接触非线性的引入,使有限元计算工作量增大,而理论公式的计算比有限元法简单方便,更适合工程设计人员使用。
[ 1 ] 吴林峰, 尹晓春. 转炉用变截面自平衡式扭力杆扭转变形的理论计算[J]. 工程力学, 2012, 29(6): 47-51. WU Linfeng, YIN Xiaochun. Calculation formala for torsional deformation of self-balanced torsion bar with variable cross-section in convertor [J]. Engineering mechanics, 2012, 29(6): 47-51.
[ 2 ] LEE K. A numerical method for dynamic analysis of tracked vehicles of high mobility [J]. Journal of Mechanical Science and Technology, 2000, 14 (10): 1028-1040.
[ 3 ] 余杨, 高瞻. 转炉旋转接头扭力杆防旋转装置及有限元分析[J]. 钢铁技术, 2010(1): 8-12. YU Yang, GAO Zhan. Finite element analysis of the anti-rotation device of rotary joint torsion bar in convertor [J]. Iron & Steel Technology, 2010(1): 8-12.
[ 4 ] BARTHELAT F, WU Z, PROROK B C, et al. Dynamic torsion testing of nanocrystalline coatings using high-speed photography and digital image correlation [J]. Experimental Mechanics, 2003, 43(3): 331-340.
[ 5 ] 刘春节, 王正东. 圆形截面微型扭杆刚度的解析计算[J]. 工程力学, 2009, 26(7): 35-38. LIU Chunjie, WANG Zhengdong. Analysis of torsion rigidity of micro bars with circular cross section [J]. Engineering Mechanics, 2009, 26(7): 35-38.
[ 6 ] 赵燕. 全悬挂转炉扭力杆和耳轴的扭转刚度分析[J]. 北京联合大学学报(自然科学版), 2012, 26(2): 25-29. ZHAO Yan. Torsion stiffness analysis of torque rod and trunnion for full suspension convertor [J]. Journal of Beijing Union University(Natural Sciences), 2012, 26(2): 25-29.
[ 7 ] 张义民, 贺向东, 刘巧玲. 扭杆的可靠性优化设计[J]. 汽车技术, 2002 (5): 5-7. ZHANG Yimin, HE Xiangdong, LIU Qiaoling. Reliability design of torsion bar diameter [J]. Automobile Technology, 2002(5): 5-7.
[ 8 ] 郑龙捷. 转炉扭力杆工作过程异常振动原因分析与改进措施[J]. 冶金丛刊, 2013(5): 37-41. ZHENG Longjie.Analysis on abnormal vibration of torsion bar device during operation and countermeasures [J]. Metallurgical Collections, 2013(5): 37-41.
[ 9 ] 齐坚, 陶海银. 国内容量最大的全国产化下悬挂转炉投产成功应用多项中冶赛迪自主技术[J]. 中国钢铁业, 2009(5): 31. QI Jian,TAO Haiyin. The successful application of independent technology CISDI in Hanging converter with the domestic production capacity of the largest one in the national production [J]. China Steel, 2009(5): 31.
[10] 吴林峰. 转炉托圈和扭力杆的设计理论分析[D]. 南京:南京理工大学,2012.
[11] 徐铭陶, 周荣仁, 赵邦义. 振动分析基础讲义[M]. 重庆:重庆大学力学教研室, 1982.
[12] 张阿舟, 诸德超, 姚启航, 等. 振动理论与分析[M]. 北京:航空工业出版社, 1996.
[13] 吴福光, 蔡成武, 徐兆. 振动理论[M]. 北京: 高等教育出版社, 1987.
[14] MOAVENI S. Finite element analysis—theory and application with ANSYS[M]. 3rd ed. Beijing: Electronic Industry Press, 2008.
Vibration analysis on the torsion bar system in convertors
WU Linfeng,WANG Wen
(School of Mechanical Engineering, North China University of Water Resources and Electric Power, Zhengzhou 450008,China)
The dynamic characteristics of torsion bar system have an important impact on the reliability of convertors, and its natural frequencies and mode shapes are consequently crucial for the independent innovation of the device. Four models were proposed for the torsion bar system. They are antisymmetric bending vibration models made up of homogeneous beam or concentrated mass beam with different boundary conditions: hinged at one end and simply supported at the other, or clamped at one end and simply supported at the other. A 150-ton Oxygen Top Convertor in a certain factory was taken as an example for the study using the four models proposed. The results show that the model of concentrated mass beam which is clamped at one end and simply supported at the other is more reasonable than the other three. The analytical solution was verified by the finite element method. The analytical results and numerical results are in good agreement and both methods are valid in the design, whereas the analytical method is more convenient and subsequently more suitable for engineering applications. The results provide a theoretical basis for the design and production of convertors.
convertor; torsion bar system; vibration beam model; theoretical solution; finite element solution
河南省科技厅科技攻关计划项目(152102210110);华北水利水电大学高层次人才科研启动项目;华北水利水电大学教学名师培育项目
2015-11-25 修改稿收到日期: 2016-02-21
吴林峰 女,博士,教授,1970年3月生
TB121; TF748.2
A
10.13465/j.cnki.jvs.2017.06.014
