非整周期采样信号相位差估计的相频匹配方法
2017-04-11涂亚庆沈艳林沈廷鳌陈宝欣
涂亚庆, 沈艳林,2, 沈廷鳌, 陈宝欣
(1.后勤工程学院 信息工程系, 重庆 401311; 2.武警后勤学院 军交运输系,天津 300000)
非整周期采样信号相位差估计的相频匹配方法
涂亚庆1, 沈艳林1,2, 沈廷鳌1, 陈宝欣1
(1.后勤工程学院 信息工程系, 重庆 401311; 2.武警后勤学院 军交运输系,天津 300000)
为提高信号非整周期采样条件下相位差的估计精度,改善方法的抗噪性能,提出一种非整周期采样信号相位差估计的相频匹配方法。该方法通过两路正弦信号的分段Hilbert变换、互相关、自相关、相位加权平均等技术获得两路信号的相位差。理论分析表明,分段Hilbert变换有效抑制了正弦信号非整周期采样对Hilbert变换的影响。仿真实验结果表明,与互相关法、Hilbert变换法、数据延拓式相关法相比,该方法改善了非整周期采样信号的相位差估计方法的抗噪性能,提高了相位差的估计精度,其相位差估计误差更接近克拉美罗下限。科氏流量计流量检测实验证实了该方法的有效性。
相位差估计;相频匹配;非整周期采样;分段Hilbert变换
正弦信号的相位差估计广泛应用于导航定位、雷达、声呐、通讯和仪表装置等领域[1-5],具有重要的研究意义和应用价值。例如,科氏流量计就是通过估计两路正弦信号之间的相位差获得流体的质量流量。因此,提高正弦信号的相位差估计精度有助于改善科氏流量计的计量精度。
为获得两路正弦信号的相位差,过零检测法[6]通过计算两路正弦信号过零时刻的时间差获得相位差。该方法计算量小,测量速度快,但抗噪性能较差,尤其对二次谐波敏感。互相关法[7-8](Cross-correlation Method, CM)利用两路正弦信号时延为零的互相关信号和自相关信号获得相位差估计值。该方法无需预知信号的频率即可获得两路正弦信号的相位差,但是其相位差估计性能受信号非整周期采样影响较大。为抑制信号的非整周期采样对互相关法的影响,数据延拓式相关法[9](Data Extension-based Correlation Method, DECM)通过对两路正弦信号进行数据延拓,使数据延拓信号接近整周期采样,然后利用互相关法获得相位差估计值。该方法有效抑制了信号非整周期采样的影响,但是由于该方法仍需通过两路正弦信号时延为零的自相关信号计算相位差,所以其抗噪性能较差。为提高相位差估计方法的抗噪性能,Hilbert变换法[10-12](Hilbert Transform, HT)通过对两路正弦信号进行Hilbert变换,得到解析信号,通过解析信号时延为零的互相关信号获得信号的相位差。该方法原理简单,但是受Hilbert变换端点效应和互相关信号有效信息利用不充分的影响,相位差估计精度有待进一步提高。
针对信号非整周期采样导致相位差估计精度较差的问题,为改善相位差估计方法的抗噪性能,提高相位差的估计精度,提出一种非整周期采样信号相位差估计的相频匹配方法。该方法通过信号频率估计值确定分段Hilbert变换的最优矩形窗窗函数长度,通过分段Hilbert变换抑制正弦信号非整周期采样对Hilbert变换的影响;为提高方法的抗噪性能,基于相频匹配原理,利用互相关信号和自相关信号的相频匹配获得两路正弦信号的相位差。
1 相频匹配方法
1.1 实验设备
设有两路信号为
(1)
式中,sx(n)=Acos(ωn+θ1),sy(n)=Bcos(ωn+θ2),为便于叙述,本文将sx(n)和sy(n)称为两路正弦信号。ω、N分别为两路信号的圆周频率和信号长度,A和B分别为两路信号的幅值,θ1和θ2分别为两路信号的初相位,z1(n)和z2(n)分别为两路正弦信号的噪声。
为抑制信号非整周期采样对相位差估计的影响,提高相位差估计精度,提出一种非整周期采样信号相位差估计的相频匹配方法,方法的基本思想如图1所示。首先,对两路正弦信号进行分段Hilbert变换,抑制正弦信号非整周期采样对Hilbert变换的影响。其次,对解析信号进行互相关和时域平均,获得互相关信号。然后,对解析信号进行自相关和时域平均,获得自相关信号,实现自相关信号和互相关信号的频率匹配。最后,对互相关信号和自相关信号进行互相关,得到互相关函数,利用互相关函数相位的加权平均获得两路正弦信号的相位差。

图1 方法原理图Fig.1 Main idea of the proposed method
为有效抑制信号非整周期采样对正弦信号Hilbert变换的影响,根据信号频率估计值计算最优矩形窗窗函数长度,通过对信号加矩形窗进行分段,并对分段信号进行Hilbert变换,抑制正弦信号Hilbert变换的端点效应,为提高相位差估计精度创造有利条件。当分段信号为整周期采样信号时,其Hilbert变换不存在端点效应,为无失真信号。
证明:
利用DFT计算采样信号s(n)=Acos(ωn+θ)的解析信号的步骤为:
对s(n)做DFT,得:
(2)
令
(3)
对Z(k)做逆DFT,得:
(4)

当k=k1(k为整数)时,式可以化简为
(6)
为了使两路正弦信号接近整周期采样,通过计算矩形窗窗函数长度对信号进行分段,最优窗长度L0应满足式(7)。
δL0=min{δL}
(7)
(8)
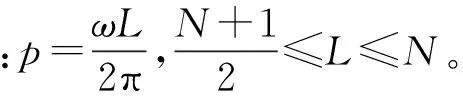
分别将两路正弦信号分成两个长度均为L0的分段信号xm和ym(m=1,2),如式(9)、(10)所示。
(9)
(10)
对分段信号xm和ym进行Hilbert变换,获得对应的解析信号xmh和ymh。
为获得两路正弦信号的相位差,对xmh和ymh进行互相关,得互相关信号为
(11)
互相关信号的期望值为
(12)
由式可知,分段信号的互相关信号rxy1和rxy2具有相同的初相位和频率。因此,为提高互相关信号的信噪比,对rxy1和rxy2进行时域平均,获得互相关信号rxy为
(13)
式中k=0,1,…,L0-1。
互相关信号rxy(k)的期望值为
(14)
由式(14)可知:零序号(k=0)互相关信号及其以外(k>0)互相关信号的相位均含有相位差信息,充分利用零序号以外互相关信号能够有效改善方法的抗噪性能,有助于提高相位差的估计精度。为消除互相关信号未知频率对相位差估计的影响,对xmh和ymh进行自相关和时域平均,得到xmh和ymh的自相关信号rss为
(15)
自相关信号的期望值为
(16)
式中:k=1,2…,L0-1,并取rss(0)=1。
由式(16)可知:自相关信号的频率与互相关信号频率相同,即自相关信号与互相关信号频率匹配,而且自相关信号具有确定的初相位——零初相位。
根据式(14)和(16)可得:
angle(rxy(k))=
angle(rss(k))+Δθ=anglerss(k)+θ2+θ1
(17)
由式(17)可知,当自相关信号的补偿相位Δθ等于两路正弦信号的相位差时,相位补偿后的自相关信号与互相关信号相位匹配。因此,为获得两路正弦信号的相位差,对互相关信号rxy和自相关信号rss进行互相关,获得互相关函数,利用互相关函数相位的加权平均获得两路正弦信号的相位差为
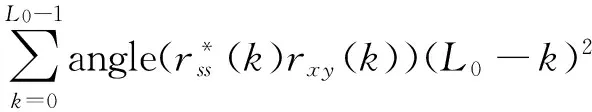
(18)
由上述分析可知,本文方法基本流程为:①计算信号的频率估计值ω1;②利用式(7)~(10)对两路正弦信号进行分段,获得分段信号xm和ym,并对xm和ym进行Hilbert变换获得解析信号xmh和ymh;③利用式(13)计算xmh和ymh的互相关信号rxy;④利用式(15)计算xmh和ymh的自相关信号rss;⑤利用式(18)计算相位差估计值Δθ。
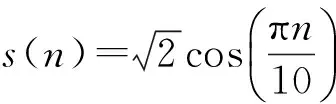
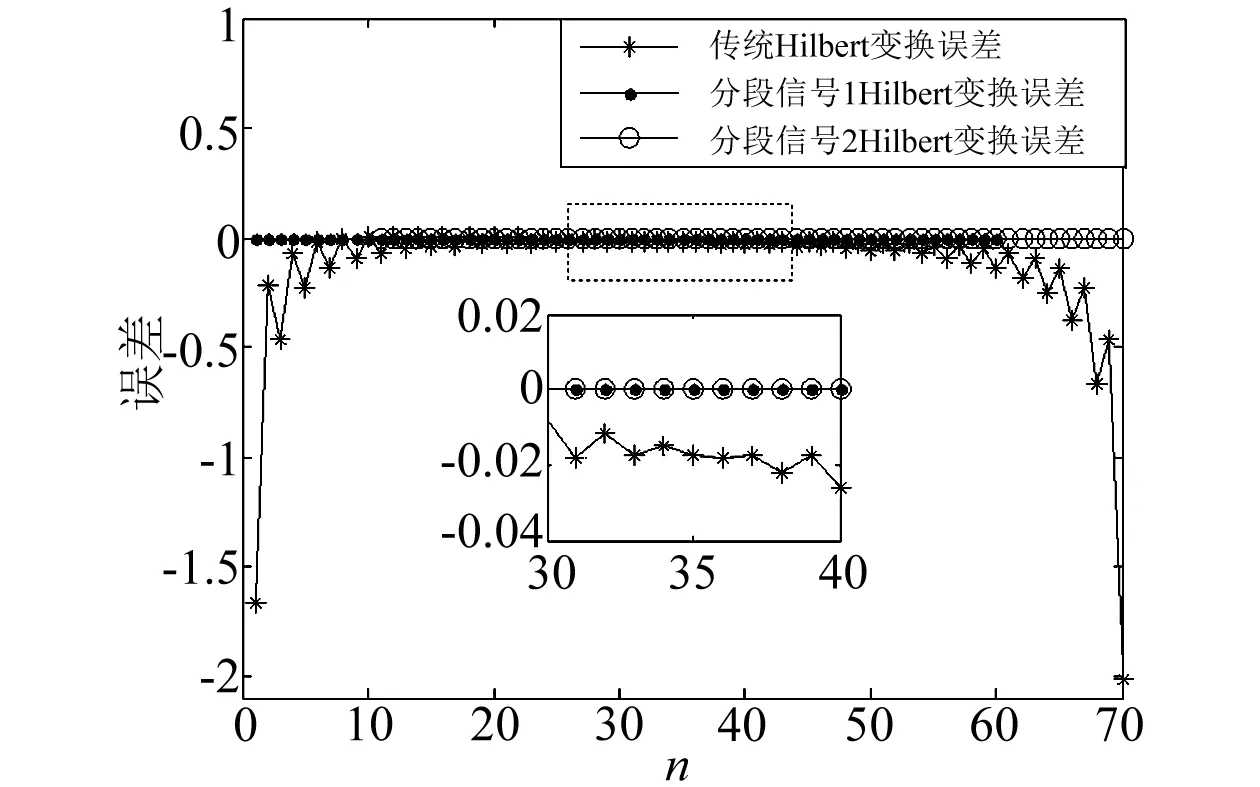
图2 正弦信号Hilbert误差图Fig.2 Error of sinusoidal signals’ Hilbert transform
由图2可知:正弦信号的传统Hilbert变换与理论值存在一定的误差,尤其是在靠近信号两端时,误差明显增大。本文提出的正弦信号分段Hilbert变换更接近正弦信号Hilbert变换理论值,说明分段Hilbert变换有效抑制了信号非整周期采样对Hilbert变换的影响。因此,正弦信号的分段Hilbert变换能够从信号源头上为提高信号的相位差估计精度创造有利条件。
2 仿真实验
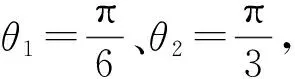
2.1 不同信噪比条件下的仿真实验


图3 不同信噪比条件下的相位差估计误差Fig.3 MSE of phase difference estimation versus SNRs
2.2 不同信号长度条件下的仿真实验


图4 不同信号长度条件下的相位差估计误差Fig.4 MSE of phase difference estimation versus N
由实验结果可知:受信号非整周期采样的影响,互相关法和Hilbert变换法的相位差估计误差呈周期衰减振荡趋势:HT方法相位差估计误差的振荡周期约为2π/ω,且当信号频率Νω/(2π)≈m(m为整数),即采样信号接近整周期采样时,Hilbert变换方法的相位差估计误差较小。由于互相关法的互相关信号误差项为倍频信号的累加和,所以其相位差估计误差的振荡周期约为π/ω,为Hilbert变换方法相位差估计误差的振荡周期的一半。本文方法和数据延拓式相关法的相位差估计精度随着信号采样点数的增加不断提高,几乎不受信号非整周期采样的影响,且本文方法的相位差估计精度明显好于数据延拓式相关法的相位差估计精度。
3 实验验证
为验证本文方法对提高科氏流量计计量精度的实际贡献,利用课题组自制的科氏流量计实验平台进行流量测量实验。选用的科氏流量计为RHEONIK科氏流量计,其变送器型号为RHE08型,流量计振动信号的频率约为146 Hz,采样频率为10 kHz,信号采样点数为2 000,质量流量测量范围为1.0~13 kg/min,实验结果如表1所示。
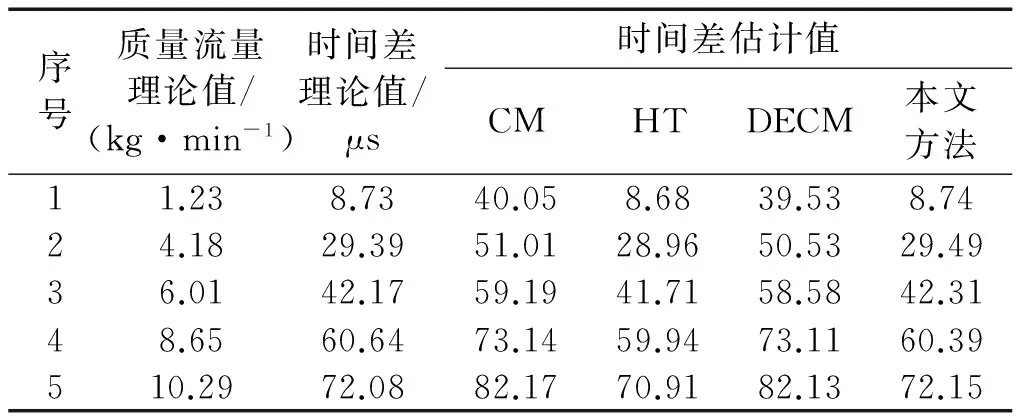
表1 不同流量条件下的时间差估计值Tab.1 Estimated time delays under different flow rates
由表1可知,本文方法的时间差估计值更接近于时间差理论值,优于互相关法、Hilbert变换法和数据延拓式相关法,尤其是互相关法和数据延拓式相关法,说明本文方法能够有助于改善相位差估计精度,提高科氏流量计的计量精度。
4 结论
为提高非整周期采样条件下的相位差估计精度,本文提出了一种非整周期采样信号相位差估计的相频匹配方法。该方法通过分段Hilbert变换有效抑制了Hilbert变换的端点效应,克服了信号非整周期采样对相位差估计的影响;通过互相关信号和自相关信号获得互相关函数,利用互相关函数的相位加权平均改善了相位差估计的抗噪性能,提高了相位差估计精度。仿真实验和科氏流量计流量测量实验验证了本文方法的优越性和有效性。
[ 2 ] GEDALYAHU K, ELDAR Y C. Time-delay estimation from low-rate samples: a union of subspaces approach[J]. IEEE Transactions on Signal Processing, 2010, 58(6): 3017-3031.
[ 3 ] TAO R, ZHANG W Q, CHEN E Q. Two-stage method for joint time delay and Doppler shift estimation[J]. IET Radar Sonar Navigation, 2008, 2(1): 71-77.
[ 4 ] MASKELL D L, WOODS G S. The discrete-time quadrature subsample estimation of delay[J]. IEEE transactions on Instrumentation and Measurement, 2002, 51(1):133-137.
[ 5 ] SO H C. A comparative study of two discrete-time phase delay estimators [J]. IEEE Transactions on Instrumentation and Measurement, 2002, 54(6):2501-2504.
[ 6 ] 任海东, 尹文庆, 胡飞. 基于LabVIEW的三种相位差测量法的对比分析[J]. 科学技术与工程, 2010(1): 263-268. REN Haidong, YIN Wenqing, HU Fei.Contrast and analysis of three measuring methods for phase difference based on labview[J]. Science Technology and Engineering, 2010(1): 263-268.
[ 7 ] SHASWARY E, TAVAKKOLI J, XU Y. A new algorithm for time-delay estimation in ultrasonic echo signals[J]. IEEE transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2015, 62(1): 236-241.
[ 8 ] 李建民, 赵鹏, 侯文, 等. 基于相关理论的相位差算法的误差研究[J]. 中北大学学报(自然科学版), 2009, 30(6): 616-619. LI Jianmin, ZHAO Peng, HOU Wen, et al. Research on error of phase difference algorithm based on correlation theory[J]. Journal of North University of China(Natural Science Edition), 2009, 30(6), 616- 629.
[ 9 ] 沈廷鳌, 涂亚庆, 李明, 等. 数据延拓式相关的相位差测量方法及验证[J]. 仪器仪表学报, 2014, 35(6): 1331-1337. SHEN Ting’ao, TU Yaqing, LI Ming, et al. Research and validation on improved correlation method for phase difference measurement based on data extension[J]. Chinese Journal of Scientific Instrument, 2014, 35(6): 1331-1337.
[10] 刘维来, 赵璐, 王克逸,等. 基于希尔伯特变换的科式流量计信号处理[J]. 计量学报, 2013, 34(5): 446-451. LIU Weilai, ZHAO Lu, WANG Keyi, et al. Signal processing for Coriolis mass flowmeter based on Hilbert transform[J]. Acta Metrologica Sinica, 2013, 34(5): 446-451.
[11] 杨辉跃,涂亚庆,张海涛,等. 一种基于SVD和Hilbert变换的科氏流量计相位差测量方法[J]. 仪器仪表学报, 2012,33(9):2101-2107. YANG Huiyue, TU Yaqing, ZHANG Haitao, et al. Phase difference measuring method based on SVD and Hilbert transform for Coriolis mass flowmeter[J]. Chinese Journal of Scientific Instrument, 2012, 33(9): 2101-2107.
[12] TU Yaqing, YANG Huiyue, ZHANG Haitao, et al. CMF signal processing method based on feedback corrected ANF and Hilbert transformation [J]. Measurement Science Review, 2014, 14(1):41-47.
Phase and frequency matching based phase difference estimation method for non-integer periods sampling signals
TU Yaqing1, SHEN Yanlin1,2, SHEN Ting’ao1, CHEN Baoxin1
(1.Department of Information Engineering,Logistical Engineering University,Chongqing 401311,China;2.Military Traffic and Transportation Department, Logistics College of CAPF, Tianjin 300000,China)
To improve the precision and anti-interference performance of phase difference estimation for non-integer periods sampling signals, a phase and frequency matching based phase difference estimation method was proposed. The phase difference estimation was obtained by means of the segmented Hilbert transform to suppress the effect of non-integer periods sampling sinusoidal signals on the Hilbert transform. The simulation results demonstrate that compared with the methods of cross-correlation, Hilbert transform and data extension-based correlation, the proposed method has better phase difference estimation performance for non-integer periods sampling signals in terms of its estimation precision and anti-interference performance. Its phase difference estimation errors are closer to Cramer-Rao lower bound (CRLB). The measurement experiments on the flow rates of Coriolis mass flowmeter validate the effectiveness of the proposed method.
phase difference estimation; phase and frequency matching; non-integer periods sampling; segmented Hilbert transform
国家自然科学金(61271449;61302175);重庆市自然科学基金(CSTC2015jcyjBX0017);重庆市研究生科研创新项目(CYB14100)
2015-08-21 修改稿收到日期: 2016-01-31
涂亚庆 男,博士,教授,1963年生
沈艳林 男,博士生,1987年生
TM933.3
A
10.13465/j.cnki.jvs.2017.06.002
