积累经验促发展——数学活动课《探寻宝藏位置的秘密》教学实践与思考

余桂敏

【教学内容】

《探寻宝藏位置的秘密》（适合五、六年级学生）

【教学过程】

一、提出数学问题，激活已有经验

1.揭示主题：这节课我们一起来《探寻宝藏位置的秘密》。

2.思维热身操。

（1）线上的位置。

师：宝藏和这三个彩球的位置有关系，找到它们的位置就能找到宝藏哦！

生：红球在第5个，黄球在第10个，蓝球在第15个。

（2）平面上的位置。

师：这三个彩球落在了草地上，它们分别在哪个位置？

生：最好有格子图，就可以用数对来表示位置。（出示坐标图）

师：你的方法真好，确定位置要找到一个标准，我们可以借助格子图。现在能说说三个彩球分别在什么位置了吗？

生：红球在（1，5），黄球在（3，2），蓝球在（7，4）。

师：用数对可以表示位置，平面上的点在第几列第几行。

（3）复习八个方向。

师：宝藏藏在黄球的某个方向，猜猜会在哪儿？有几种可能？

生：都有可能！

师：哦，八个方向都有可能。（出示蓝球：宝藏在我的西北方向）瞧，宝藏在红球的什么方向？在黄球的什么方向？

二、自主探索策略，丰富活动经验

1.师生游戏，了解规则。

（出示10×10的方格图）

师：老师已经想好了一个点藏宝藏，谁来猜猜？

生：（点某个点）宝藏在这里。

师：不对，宝藏在你的西南方，继续猜……（根据学生的猜测，让学生体会交叉分析，缩小范围的过程）

师：大家想玩这样的游戏吗？我们再熟悉一下游戏规则。

出示规则：

（1）同桌合作，一人设定宝藏的位置，另一人进行猜测。

（2）设定宝藏的同学根据同桌的猜测，给出提示：不对，宝藏在你的××方。

（3）最多猜五次，游戏结束。

（4）同桌互换角色，继续猜。

（5）想一想，怎样才能保证猜的次数最少？

2.同桌活动，教师巡视。

3.同桌演示，交流提升。

（展示两组没有游戏策略，猜的次数较多的游戏过程）

师：有没有猜的次数少一些的同学？

生 1：我猜宝藏在（5，5）。

生2：宝藏在你的西南方向。

生 1：（2，2）？

生2：宝藏在你的东南方向。

生 1：（3，1）？

生2：宝藏在你的正东方向。

生 1：（4，1）？

生2：对了！

师：发现他们的好方法了吗？

生：猜的都是中心点。

师：这样猜有什么好处呢？

生：先猜最中间的点，可以缩小范围。比如，先找（0，0）点的话，东北方向还有一大片，还是很难找。先找（5，5）这个点，就把方格分成了四块。

师：大家有疑问吗？

生：那放这边，比如（3，5）这个点，不是也分成四块了？

生：如果在东南方向，这个区域就特别大，不好找。先找（5，5）这个点，就把方格等分成了四块。那么接下来无论在哪个方向，范围都小了。

师：他的意思是？

生：平均分成四份，每份区域一样大。

师：如果宝藏在西南方向，我们也要找到它的中心点，在哪？

生：（2，2）。

师：看来利用中间位置是个好方法，这样可以把区域等分，使每一区域剩下的面积都尽可能小。

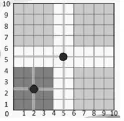
师：那如果提示是在正方向上，比如正北方向，怎么思考？

生：也只要先猜中心位置。

4.策略应用。

（1）再次活动。

师：用这个办法再想一想：最多几次能保证猜中呢？

（强调：每次都要找可能区域的中心位置）

生：一次。

师：你们同意吗？

生：一、两次就猜中是运气好，不是每次都会成功的。

师：那一般情况下，至少几次能保证一定猜中呢？（请学生选点说明：无论哪个区域，只要每次都找它的中心位置，保证最多四次就能猜到）

（2）推广更大范围。

师：现在加大方格图（20×20），第一次应该猜哪？最少几次能保证猜中？我们再验证一下。

生：最多五次。

师：现在区域扩大到原来的四倍了，为什么猜的次数只增加一次就够了？

生：只要加第一次（10，10）中心点后，就变成原来的情况了！

师：如果扩大到40×40的方格图，先找哪个点？需要几次？80×80的呢，先找哪个点？又需要几次？你发现了什么？

生：都是先找中间点，缩小范围，转化成前面的大小，比之前的多加一次就好。

三、挑战游戏任务，提升活动经验

1.三维空间位置表示，构建魔方模型。

师：确定一个物体的位置，在一条线上，按顺序数可以找到它；在一个面上，用数对来表示它；现在这三颗球跑到了这个空间中，我们又该怎么表示它们的位置呢？

生：用三个数来表示！两个数表示列和行，现在不够了，还要表示出层（高）。

师：有道理！我们可以先考虑列，再考虑行，最后考虑层（高），这个很像魔方，我们可以借助魔方来给它定位。

2.表示魔方上的宝藏位置。

师：瞧，宝藏就藏在魔方的这个位置，该怎么表示呢？先自己想一想，再和同桌讨论一下。说说你的想法。

生：宝藏在第4列，第1行，第4层，所以我觉得可以用（4，1，4）表示。

3.借助媒体分解演示说明。

师：我们来分解一下吧！4表示列数，1表示行数，第三个数“4”表示的是层数。

4.找一找。

（1）现在宝藏的位置又该怎么表示呢？（1，3，4）（4，3，3）

（2）想像一下宝藏在哪里？（3，2，4）（2，4，2）学生指一指，然后进行电脑动态展示。

四、分享活动经验，构建知识网络

师：今天我们玩了什么数学游戏？你有什么收获？

生：我们玩了寻宝游戏。知道了在平面上用数对表示位置，在三维空间要用三个数表示位置。

师：是呀，线上只要用一个数就能表示物体的位置，二维平面要用两个数来表示，三维空间则要用三个数来确定位置。

【课后反思】

数学活动课以学生活动为主要环节，以探索、合作、交流为主要学习方式，充分发挥学生在实践活动中的主体作用，能较好地帮助学生积累基本活动经验，促进其思维发展。

一、引导学生主动提问，联结新旧经验

《数学课程标准（2011年版）》中指出：“学生的学习应当是一个生动活泼的、主动和富有个性的过程。”每个学生都是独特的个体，那么在教学中，我们要基于学生已有的经验，引发学生主动思考，主动提问。本课设置了平面上的三个小球的情境，引导学生主动思考，提出需要有表示位置的“方格图”。当三个小球在三维空间，学生在已有经验的基础上思考两个量已经不能表示，设想需要三个量：行、列、层（高）来表示位置。教师基于学生的需要，适时提供“方格图”“魔方模型”帮助学生联结新旧经验，学会平面中、三维空间中表示位置的正确方法。

二、激励学生自主探索，丰富活动经验

学生是学习活动的主体，只有把时间交给学生，让他们自主活动、探索和交流，才能充分发挥他们的学习主动性，激发更大的学习潜能。在探寻宝藏的游戏过程中，学生通过几次同桌活动，一次次判断，根据同伴的提示，感受区间的变化，缩小宝藏的范围，从而推测出正确的位置。并且，利用集体合作、讨论分析，寻找游戏策略。同伴学习，主动探索，策略研究……都让学生在活动中体会探索的乐趣，在探索中丰富了基本活动经验。

三、创设梯度活动，促进思维发展

维果斯基的“最近发展区”理论指出，“教学应着眼于学生的最近发展区，为学生提供带有难度的内容，调动学生的积极性，发挥其潜能，超越其最近发展区而达到下一发展阶段的水平。”因此，教师在教学过程中，应当创设有梯度的教学活动，引发学生主动探究，合作交流。在三维空间中表示物体的位置，不是小学阶段的教学要求，但在充分探究一维线型、二维平面表示位置的活动基础上，显然，学生跳一跳，完全有潜力摘到这颗“桃子”。借助魔方模型，学生从基本的三维空间三个量表示位置开始，到表示中间块的位置，再根据数据想象具体位置……最后把一维、二维、三维表示位置的方法沟通联系，建构整个知识网络。学生在有梯度、有层次的活动中，积累了基本活动经验，也促进了思维的发展。