巧用几何直观构建精彩课堂

2017-04-08沈璟

小学教学设计(数学) 2017年12期

沈　璟

《数学课程标准（2011版）》指出：“几何直观主要是指利用图形描述和分析问题。借助几何直观可以把复杂的数学问题变得简明、形象，有助于探索解决问题的思路，预测结果。”因此，几何直观对学生而言是一种有效的学习方法，对教师而言是一种有效的教学手段。那么如何巧用几何直观，让学生更好地感知数学，理解数学，构建出精彩的数学课堂呢？

一、巧用数线，帮学生有效建模

由于小学生理性认知能力较弱,但是感性认知能力却很强。针对这一特点，新版教材将“数线”引入课堂。“数线”实际上是数轴的“雏形”，它是刻画“数”的一种直观模型，它不仅可以帮助学生体会数的顺序和比较大小，而且可以借助“数线”这把尺子进行计算：“顺着数”相当于加法，“倒着数”相当于减法。

例如，在教学《十几减8》一课时，可以先让学生借助小棒摆一摆，写出得数，然后在此基础上引导学生观察数线。左边的图呈现是从13开始一个一个往回数的过程，也就是一个一个减的过程。右边的图呈现的是分段数，先往前数3个，再往前数5个。在这一教学环节教师可适时向学生追问：“为什么要先往前数3个，再往前数5个呢？”学生在观察、讨论中很快得出自己的结论。在这里教师要充分利用数线，引导学生用数线来表达思考过程，从而帮助学生有效地建模。

二、巧用点子图，帮学生理解算理

《数学课程标准(2011版)》将“运算能力”作为10个核心概念之一重新提出,充分表明运算能力在数学教学中的地位和作用。为了让学生在计算教学中更好地理解算理,寻求合理、简捷的运算途径,新教材引入了点子图这一计算模型来帮助学生探索计算方法、理解算理。

例如，教学《两、三位数乘一位数（不进位）乘法》（三年级上册）的片断：

1.出示情境图，根据情境图提出相关乘法问题。

（引导学生提出问题：一共有多少只蚂蚁？）

2.在点子图上圈一圈、算一算，并与你的同桌说一说计算过程。

（学生动手圈一圈，尝试独立解答并与同桌交流自己的计算过程）

师：你是怎么圈的？

生1：把小蚂蚁竖着从中间平均分成两份；

生2：把小蚂蚁横着从中间平均分成两份；

生3：把小蚂蚁分成两份，一份每行10个，圈4行；另一份每行2个，圈4行。

学生思考后交流算法：

生1：把小蚂蚁竖着从中间平均分成两份，一份是6×4=24（只），两份就是：24×2=48（只）。

生2：把小蚂蚁横着从中间平均分成两份，一份是：12×2=24（只），两份就是 24+24=48（只）或24×2=48（只）。

生3：分成两部分计算，先算10×4=40（只），再算 2×4=8（只），最后算 40+8=48（只）。

3.探索乘法竖式计算方法，理解乘法竖式每一步算理。

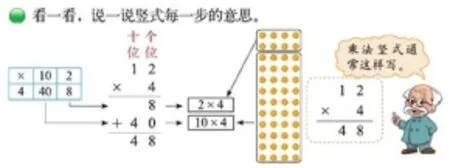
结合点子图，说一说竖式计算中每一步所表示的实际意思，即每一步求出的是点子图中的哪一部分，理解8、40、48的含义。

第一步，4乘2结果是8个点，所以8写在个位。

第二步，4个10是40个点，写在第二层，相同数位对齐。

第三步，再把8和40这两部分加在一起，得48。

在这里，小小的点子图将“冰冷”的算法和“神秘”的算理巧妙地融合在一起，让学生清楚地感受到“法中见理，理中得法”。

三、巧用画图的方法，帮学生理清数量关系

俗话说“授人以鱼不如授人以渔”。作为教师不仅要教给学生知识，更重要的是教给学生解决问题的方法。数学教学中，画图就是解决实际问题的一把金钥匙。对于复杂的、难以理解的问题，画图可以起到奇妙的作用，它可以使复杂的实际问题变得简单、直观，还可以培养学生解决问题的能力。提高学生解决问题的策略，是教学中行之有效的教学方法。

例如教学《连除和乘除混合的两步运算》（三年级下册）的片断：

1.创设情境，提出问题。

师：在买新书的活动中，你发现了哪些数学信息，你能提出什么数学问题？

生1：平均每个书架上有多少本书？

生2：2个书架一共有多少层？

生3：平均每层放了多少本书？

2.寻找解题思路。

师：请同学们尝试用自己喜欢的方法画图解决平均每个书架每层放多少本书？

（此时学生会根据情境描述，尝试用个性化的画图方法解决这个问题）