基于激光扫描法的铁路道砟级配对道床动力特性影响的离散元研究

徐 旸，高 亮，蔡小培，侯博文，赵云哲

(1.北京交通大学，土木建筑工程学院，北京 100044；2.北京市轨道交通线路安全与防灾工程技术研究中心, 北京 100044)

基于激光扫描法的铁路道砟级配对道床动力特性影响的离散元研究

徐 旸1,2，高 亮1,2，蔡小培1,2，侯博文1,2，赵云哲1,2

(1.北京交通大学，土木建筑工程学院，北京 100044；2.北京市轨道交通线路安全与防灾工程技术研究中心, 北京 100044)

铁路碎石道床的道砟级配对道床的力学性能具有显著的影响，采用三维激光扫描技术对道砟颗粒的形状特征进行了获取及分析，并提出了基于道砟外形重建结果的离散元颗粒数值模型构造方法；在此基础上建立了循环荷载道砟箱数值模型。以此研究在高速及重载线路条件下，道砟级配对散体道床动力沉降特性的影响规律，并从细观角度分析了道床的沉降机理。研究结果表明：不同运营条件下铁路碎石道床的沉降机理有所不同。道砟颗粒间的相互错动是引发重载铁路道床沉降主要原因。而对于高速铁路，道床沉降还会受到高频荷载作用下颗粒自身转动的影响。因此，建议在规范中针对不同的线路条件提出不同的道砟级配曲线要求。

铁路有砟道床； 道砟级配； 离散元法； 道床沉降； 动力响应

有砟轨道是我国铁路最主要结构形式之一，碎石道床作为有砟轨道最重要的组成部分，其服役状态是决定线路能否平稳安全运营的关键[1]。尽管我国对于350 km/h以上的高速铁路更倾向于采用无砟轨道，但在中、低速客运以及货运重载铁路中仍以有砟轨道为主要结构形式。且随着无砟轨道破坏后难以修复、在不良地质条件下的适应性等问题日益突出。有砟轨道的深化研究逐渐成为了铁路行业近年来的研究热点。

有砟轨道主要由级配碎石组成，在列车的循环荷载作用下，道砟颗粒间会发生相互错动，达到进一步的密实，从而引起道床的宏观累计沉降。当道床的累积沉降达到一定量值时，道床的弹性就会逐渐削弱，道床的排水性能也逐渐降低，进而导致行车品质下降，甚至引发道床翻江冒泥、道床板结等病害。从养护维修角度来说，散体道床的大机捣、稳作业也正是针对道床累计沉降这一问题而必须进行的日常养护维修工作。因此，延缓道床的累计沉降是确保有砟道床合理养护维修以及提高有砟道床全周期服役安全性、经济性的必然需求。对此，国内外学者开展了大量研究工作。

实验研究方面，ANDERSON等[1]通过动三轴试验研究了鼓入碎石层后道砟集料在循环荷载作用下的力学特性，认为鼓入碎石层能提高道砟集料的抗剪力学性能。胡仁伟等[2-3]采用动三轴试验对不同材质的道砟进行了研究，认为道砟材质对道砟集料力学性能影响显著，且石灰岩道砟不适用于重载铁路。INDRARATNA等[4]通过三轴试验研究了道床脏污对道砟力学性能的影响，结果表明，脏污会显著削弱道床的抗剪强度。但由于道砟颗粒本身粒径较大，动三轴试验会受到三轴室尺寸的限制，因而无法排除边界效应对实验结果的影响，且三轴试验中所采用的加载设备与真实情况中轨枕-道床的相互作用形式存在较大的区别。因此，国外学者还采用道砟箱实验开展了研究工作。Al-SAOUDI[5]通过道砟箱试验对循环荷载作用下道砟集料的沉降规律进行了研究。LIM等[6-7]则采用道砟箱实验，从细观角度研究了捣固作业对于改善散体道床累积沉降的作用。道砟箱试验虽然更接近于真实情况，但受限于加载设备，其加载频率一般在5 Hz左右，无法模拟高速铁路的高频荷载特点。

由于碎石道砟的散体特性，仅采用实验的手段无法研究道砟颗粒在循环荷载作用下的运动及接触特性，从而难以从根本上把握散体道床的细观作用机理。因此，国内外学者还建立了相应的数值模型，从理论角度开展了研究工作。LIM等[7-8]采用由8个球体组成的规则团块单元对道砟进行了模拟，并对道砟箱实验进行了数值仿真，结果表明，这种单元相比于球体单元能更好的模拟道砟颗粒间的咬合作用，但仍与真实的道砟颗粒存在较大的差别。赵金凤等[9-10]采用数个球体粘接而成的簇单元对风沙作用下道砟进行了模拟。但这种由数个球组成的道砟单元无法模拟真实道砟颗粒间的边-角接触及咬合效应，与实际情况存在较大的差别。边学成等[11-13]采用多视角投影所生成多面体对道砟进行了模拟，但由该方法所获得的扫描结果会受到被扫描时道砟颗粒摆放角度的影响，且无法对道砟颗粒底部的形状信息进行还原，因而精度有限。此外，限于计算能力，这种方法难以用于分析长期循环荷载作用下道砟的力学性能。INDRARATAN等[14]采用二维可破碎单元对循环荷载作用下的三轴试验进行了模拟，但二维的数值模型难以模拟颗粒间的三维咬合特性及空间接触机理。与真实情况差别较大。

综上所述，已有研究的不足之处主要包括如下两方面:① 传统的试验手段难以从细观角度研究在不同条件下道砟颗粒间的相互作用机理，且在尺寸、加载条件方面易受到实验设备的限制；② 已有研究表明，除道砟的级配会对道砟颗粒间的相互作用产生影响之外，道砟颗粒的形状也会对颗粒间的作用机理及咬合特性产生显著地影响，但由于现实中的道砟颗粒形状千差万别，已有的数值分析研究中，兼顾道砟颗粒的复杂外形以及道砟集料的整体级配，且从长期循环荷载作用的角度，针对道砟相互作用机理的研究十分欠缺。

为弥补上述研究不足，本文基于三维激光扫描技术，对500枚真实道砟颗粒进行了扫描，通过MATLAB自编了道砟颗粒的自填充程序以及道砟颗粒的形状特征分析程序，对颗粒样本的几何特征进行了深入分析，并基于外形分析结果，采用文献[15]所提出的相似度分析算法，选取了典型的道砟颗粒形状，对精细化道砟颗粒离散单元进行了构建；在此基础上建立了循环荷载作用下的道砟箱体数值模型，并结合已有文献中的试验结果对数值模型进行了验证；基于验证后的模型，研究了不同道砟级配对不同线路条件的适应性。

1 离散元仿真数值模型的建立

1.1 基于三维激光扫描方法的道砟颗粒外形重构

本文采用三维激光扫描仪对道砟颗粒的复杂外形进行了获取，并通过多个视角合成算法弥补了传统方法[11-13]中无法还原道砟颗粒底部形状信息的缺陷，扫描结果不受颗粒摆放角度的影响。所建立的扫描平台，如图1所示。

图1 道砟颗粒三维激光扫描平台Fig.1 3-D ballast laser scan device

本文采用自编算法对道砟三维数字重建结果进行了离散元填充，三维重建过程以及不同填充精度的道砟颗粒离散单元，如图 2所示。

(a)(b)(c)(d)(e)(f)(g)(h)

图2 精细化道砟颗粒单元的建立过程

Fig.2 Construction process of refined ballast DEM models

其中图2(a)为道砟颗粒实物图，图2(b)为通过一个视角所得到的道砟颗粒外形扫描结果，图2(c)为通过三个视角复合而成的道砟颗粒三维扫描结果，在本文的前期研究中，曾采用文献[16]中所提出的双平面镜法对道砟颗粒的三维外形进行还原，还原结果如图2(d)所示，通过与图2(c)及如图2(a)所示的原道砟颗粒进行对比，发现该方法在还原棱角系数较大的道砟颗粒时，会产生明显的误差，且无法较好的反映道砟底部的形状信息，因此本文主要采用激光扫描法作为获取道砟颗粒形状信息的主要手段。图2(e)为基于三视角激光扫描结果，并根据本文所提出的填充方法由14个球单元所组成的道砟离散元模型，图2(f)为由25个球单元所组成的道砟离散元模型，图2(g)为由41个球单元所组成的道砟离散元模型，图2(h)为由235个球单元所组成的道砟离散元模型。

1.2 颗粒的填充算法及典型道砟离散单元的建立

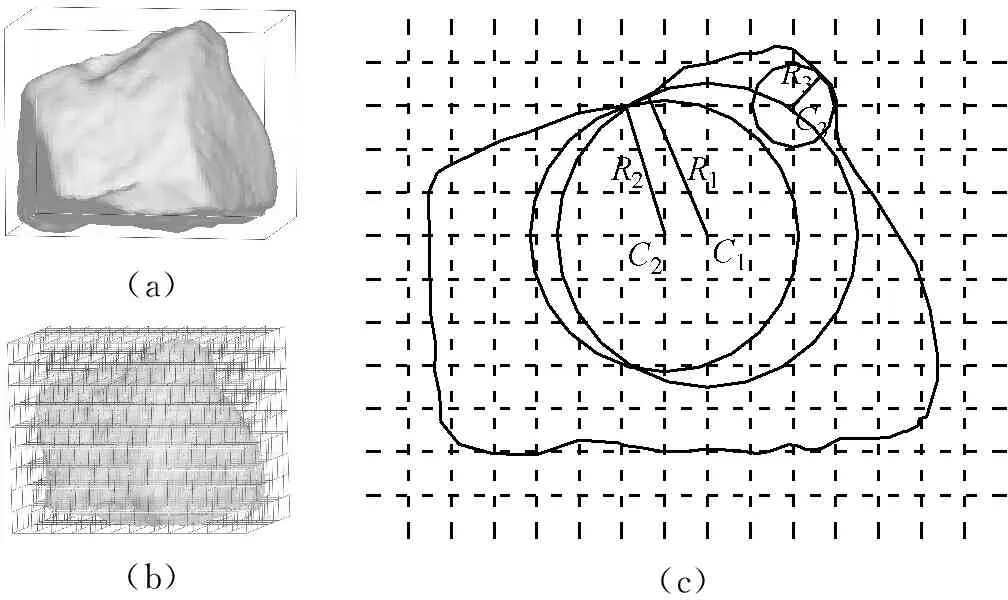
基于道砟扫描三维外形重建结果的填充算法构造过程，如图 3所示。

(a)(b)(c)

图3 道砟颗粒的三维填充方法

Fig.3 3-D ballast filling sketch

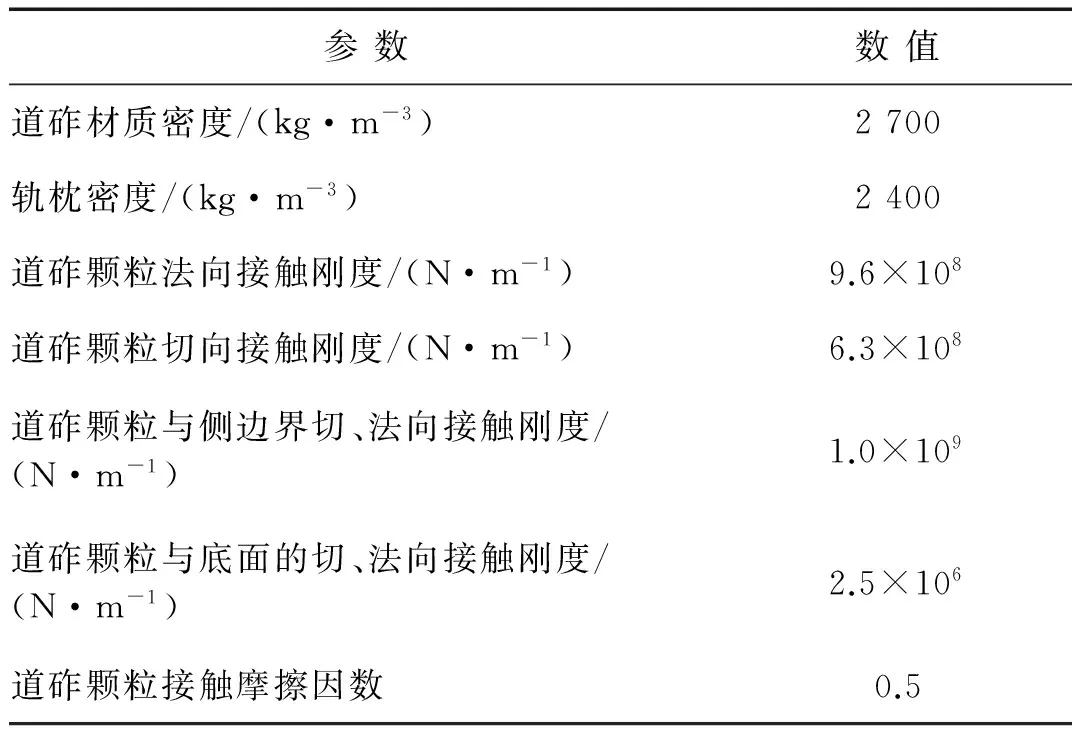
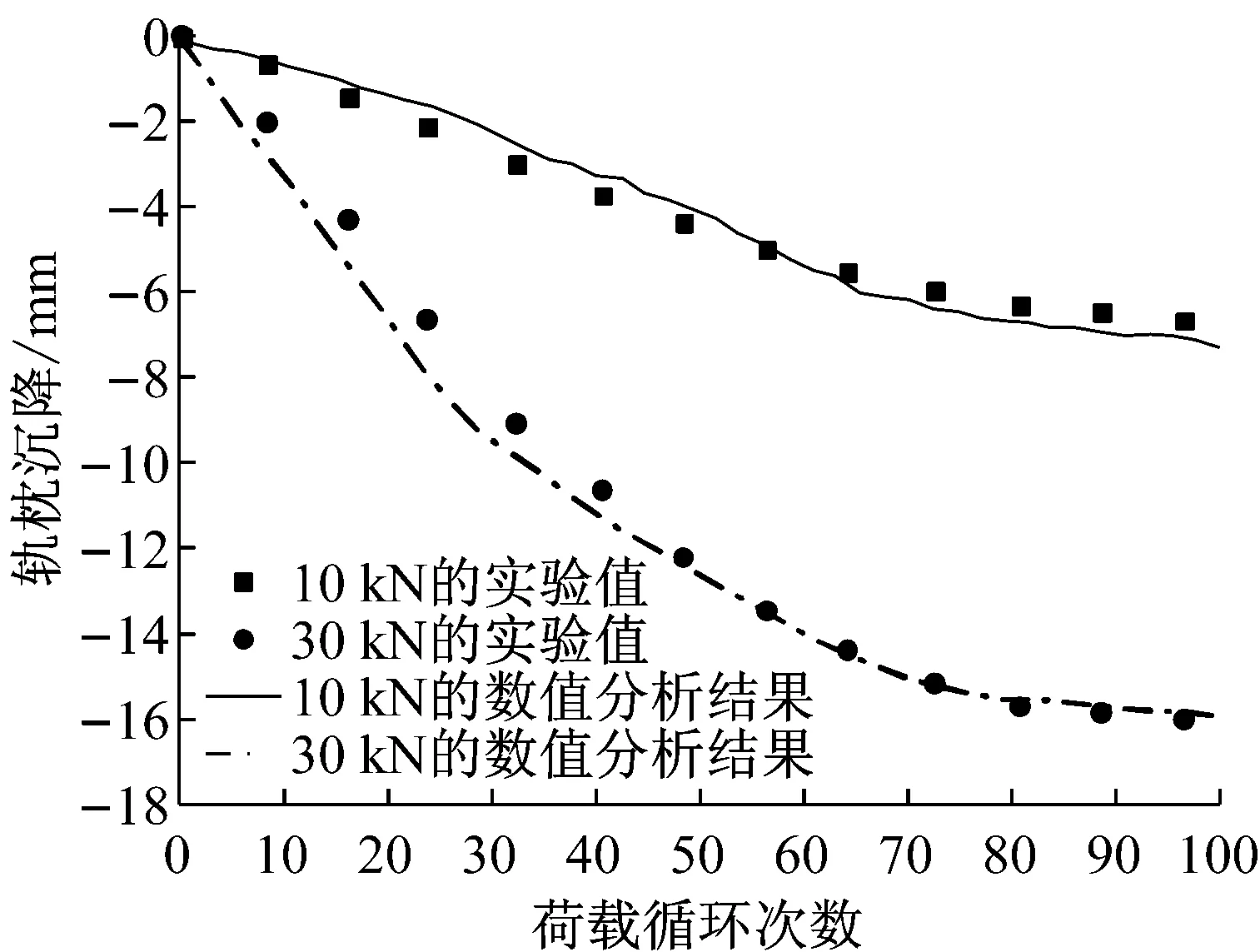
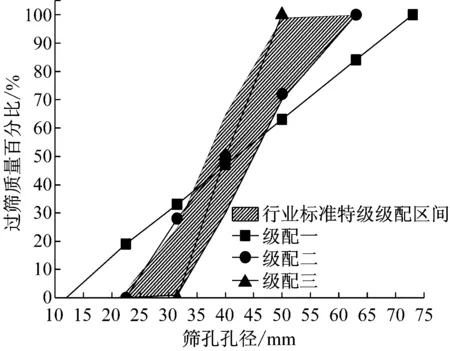
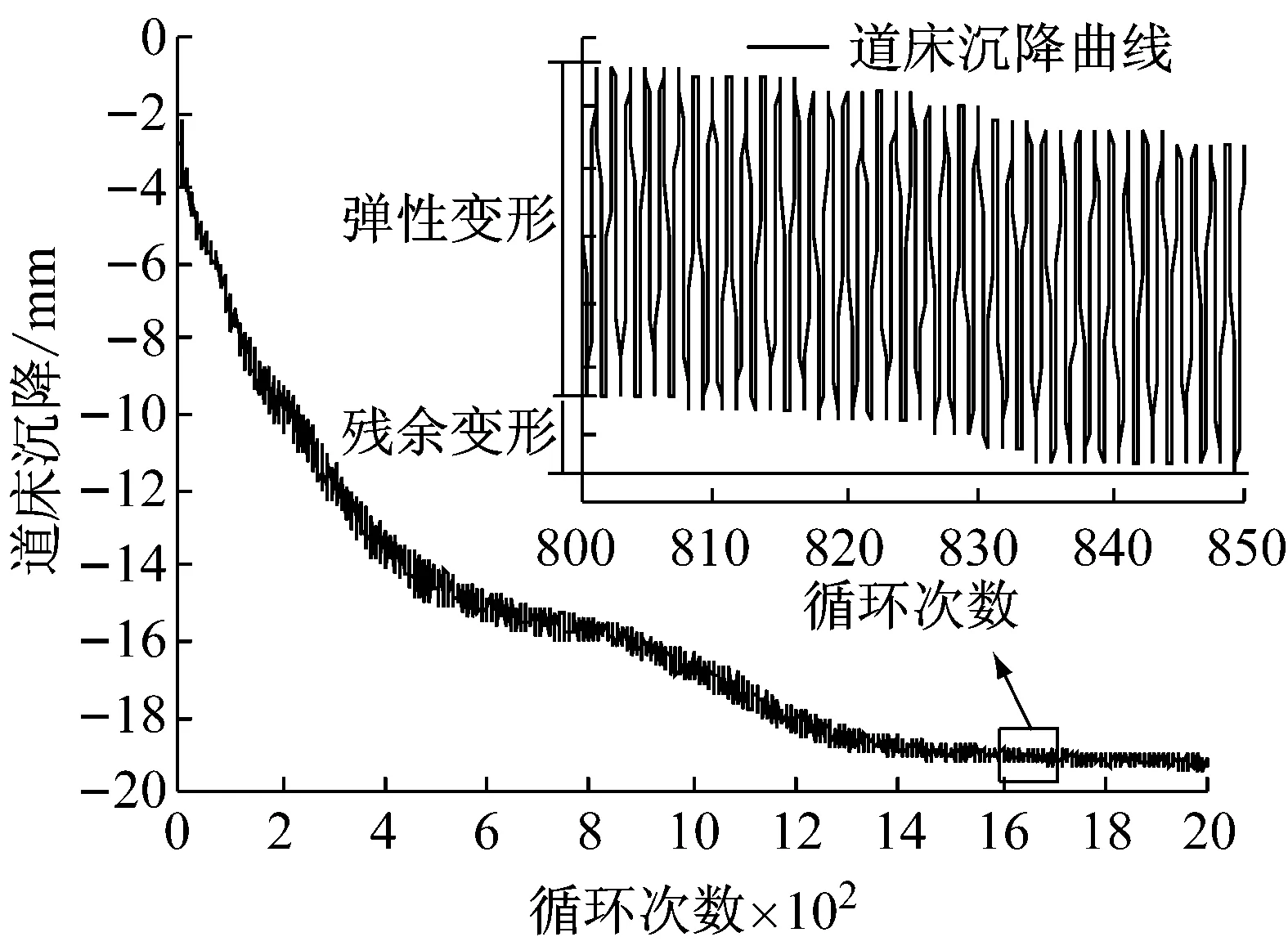
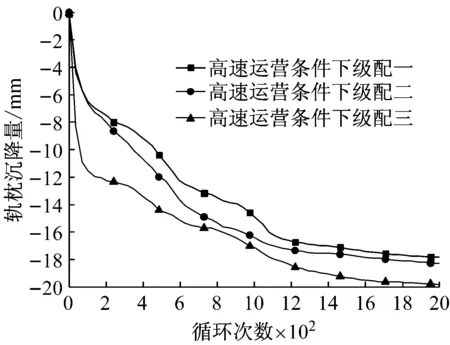
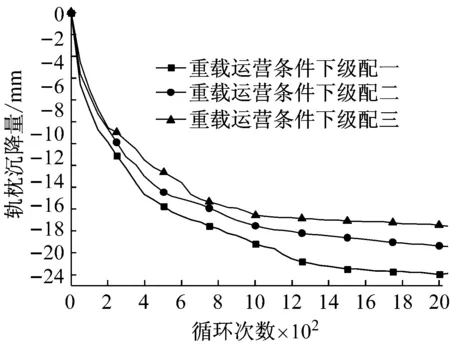
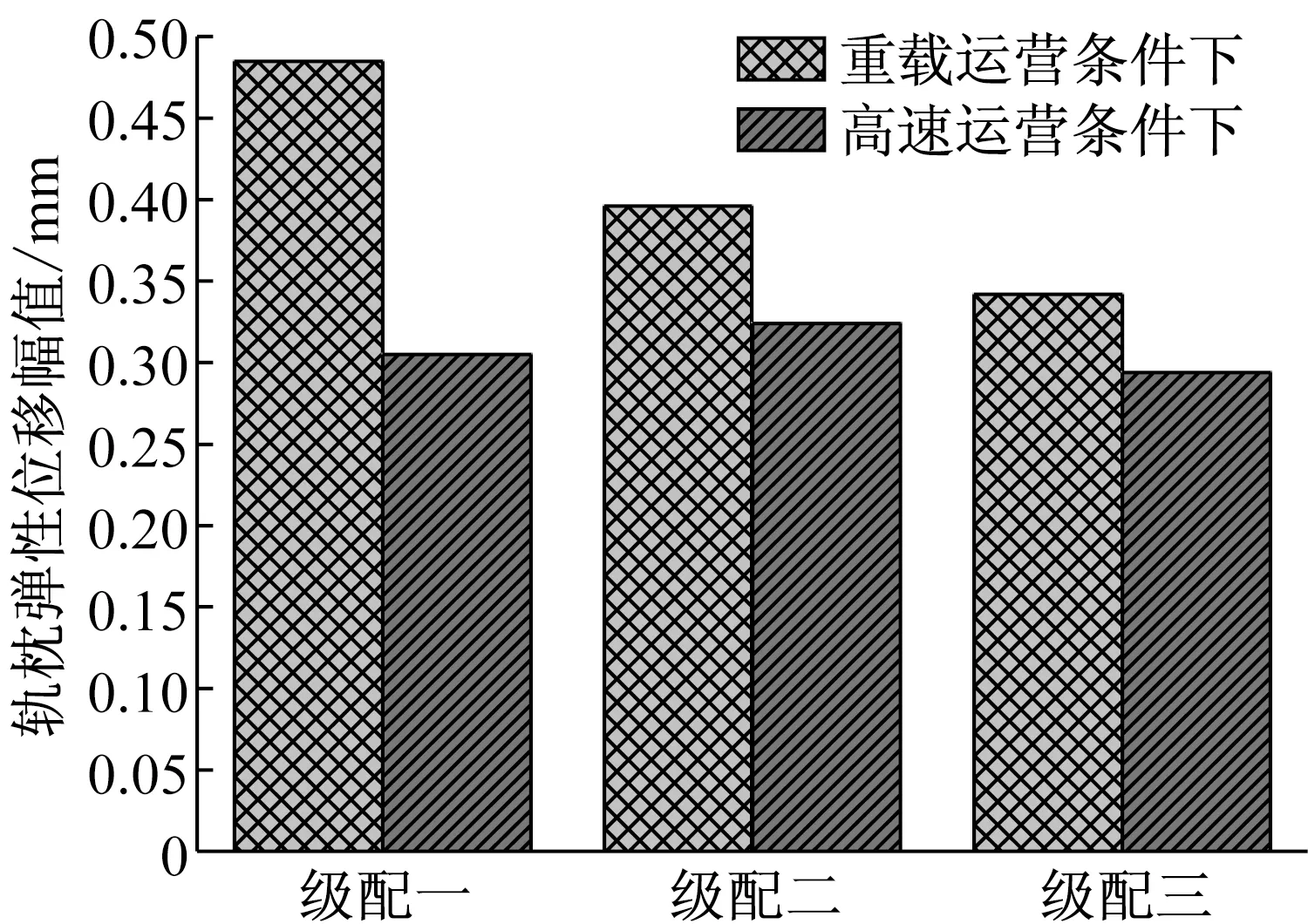
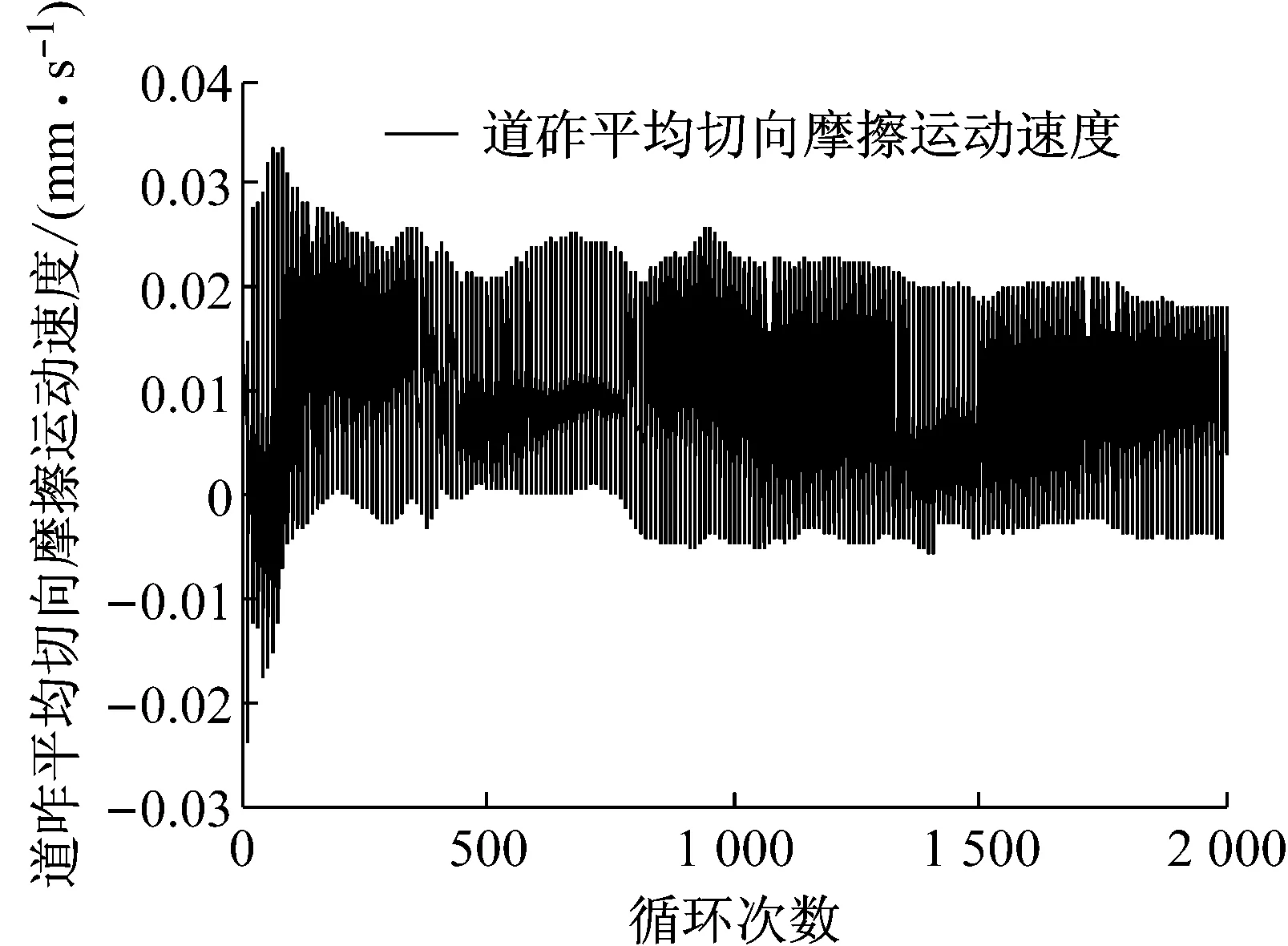
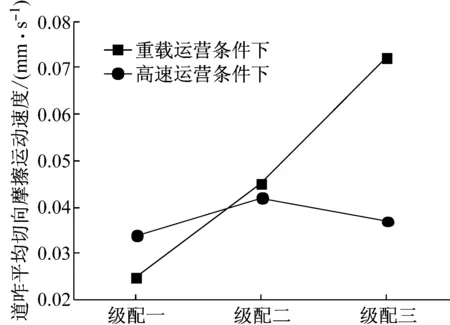
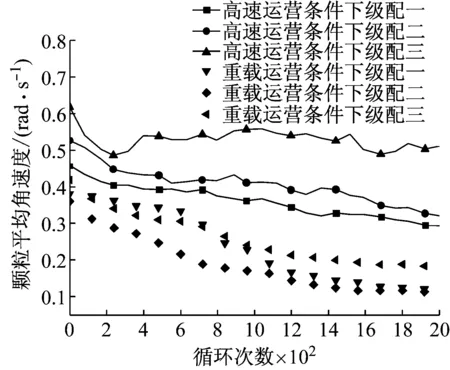
图 3(a)为道砟颗粒的三维扫描外包络空间，图 3(b)为基于颗粒的三维扫描外包络空间所建立的空间网格，网格间距为l，图 3(c)为道砟颗粒空间网格及填充球单元的二维示意图。在颗粒填充时首先选取所有位于道砟扫描结果包络空间内的网格节点，随后以节点为球心Ci(其中i为该节点的编号)，球心与道砟扫描外包络空间上的控制点连线距离最小者为半径Ri，生成球单元。以此类推，当两球单元发生重叠，且达到d

(1)

式中：h为两球中半径较小者球缺的高度，则道砟颗粒的还原精度可通过空间网格间距l、球单元的最小控制半径Rmin以及体积重叠率Cb三项参数进行控制，在Matlab程序编写时，三项控制参数的执行顺序为：① 设置空间网格间距l。② 判定所生成的球单元是否满足Ri>Rmin，如判定结果为否，则删除该球单元。③ 判定剩余小球间的重叠率是否大于控制重叠率Cbmax，如Cb>Cbmax，则删除两球中半径较小者。组合道砟颗粒的质量按照下式进行修正：

(2)

(3)

式中：M是组合道砟颗粒离散单元模型的总质量；n是构成粘接模型的球单元总数；ρb为道砟颗粒的密度；Vi是第i个球单元减去重叠部分所剩余的体积；Ri为第i个球的半径；r为与第i个球单元发生重叠的球体总数；Hq为第i个球被第q个与之重叠的小球的所截得的球缺的高。本文所提出的填充算法相比于文献[8]中基于每一道砟外包络空间上的控制点做最小半径内切球体的算法有了较大改进，大大提高运算效率。

由图 2可以看出，所采用的球单元数量越多，道砟颗粒的还原精度就越高，但过多的单元数量也会消耗大量的计算成本。本文通过大量的数值试验发现，当组合球单元的体积达到道砟扫描外包络空间体积的90%时，再增大球单元的数目对仿真精度的影响微乎其微，本文即根据这一标准对道砟颗粒的填充精度进行控制。

本文通过自编程序，按照长细比、棱角系数等形状特征，对500枚道砟颗粒进行了分析，并从中选取了16种道砟颗粒作为典型的道砟外形，如图 4所示。在模型的建立过程中，本文通过自编的道砟颗粒级配生成算法，按照颗粒粒径由小到大逐级进行生成道砟集料。在道砟颗粒的生成过程中，道砟颗粒的外形即从这16种典型颗粒中随机进行抽取。

1.3 循环荷载道砟箱数值模型的建立

本文选取了轨枕承轨槽下方700 mm×500 mm×550 mm(长×宽×高)区域进行了研究。已有研究[17]表明：容器的尺寸大于颗粒平均粒径的8倍时，容器的边界效应可以被忽略，本文各模型中颗粒的平均粒径不超过50 mm，即其最小边界要求为400 mm，而本文道砟箱的最小边界尺寸为500 mm，因此可以忽略边界效应的影响。在本文的前期研究[18]中已对不同级配下散体道床的沉降规律进行了初步探究，本文沿用了前期研究中道砟箱体模型及III型轨枕的几何参数，但对道砟颗粒数值模型进行了改进，所建立的精细化道砟离散元模型，见图 5。

由于本文所采用的道砟颗粒单元相比于前期研究已有了较大的改进。因而，本文在前期研究[18-19]的基础上，采用文献[5]中的室内实测结果对道砟颗粒的切、法向刚度两项关键参数进行了重新标定，并对模型进行了验证。

标定过程主要分为两步，首先通过采用不同的道砟颗粒切、法向刚度，对文献[5]中竖向荷载为10 kN的工况进行模拟，并将道砟的沉降曲线的仿真结果与实测结果进行对比。由于道砟切、法刚度两项参数可以任意进行匹配，因而存在多组参数能较好的模拟实测结果。因此，本文随后采用这几组参数分别对30 kN荷载作用下道砟的沉降规律进行了预测，并再次与文献中的实测结果进行了对比，仅有当某组参数能较好的模拟10 kN荷载情况下的实测结果，且同时能准确预测30 kN荷载作用下的实测结果时，则认为改套参数具有足够的准确性。通过大量的尝试，当选用表 1所示的参数时，得到的数值分析结果与实测结果对比如图 6所示。由此可认为基于表 1中的参数所建立的数值模型能较好的模拟真实情况。

表1 道砟箱离散元模型参数Tab.1 Parameters of ballast box DEM model

其中道砟颗粒与底面的切、法向接触刚度参考文献[8]进行选取。

图6 数值分析结果与实测结果对比Fig.6 Comparison of DEM and experimental results

2 不同运营条件下道砟级配对道床累积沉降的影响规律

从不同铁路运营条件的角度来说，货运重载铁路低频率、大轴重的荷载形式与客运高速铁路的高频率、低轴重的荷载形式截然不同，但我国的铁路行业标准[20]在对散体道床的颗粒级配进行规定时，仅是直观的给出了特级、一级道砟的级配、曲线区间，而并没有针对不同的线路条件，对道砟的级配适应性进行规定。这主要是由于传统的研究手段难以从根本上把握不同外荷载条件下道砟级配对颗粒间相互作用的细观影响规律。

本文即采用循环荷载道砟箱离散元数值模型针对这一问题开展研究。分别对高速和重载两种线路条件下不同级配的散体道床在循环荷载作用下的动力特性进行了分析。通过对道砟箱模型轨枕承轨槽正中钢轨作用范围内施加不同幅值与频率的循环荷载以模拟不同的线路条件。循环荷载随时间t的变化函数为

F(t)=P[cos(2πft)-1]

(4)

式中:P为荷载幅值系数；f为荷载频率系数；通过这两项参数控制输入荷载的幅值与频率。本文取高速条件下循环荷载的幅值及频率分别为24 kN和39 Hz，在重载条件下循环荷载的幅值及频率分别为59 kN和14 Hz。

为研究级配曲线取值范围对散体道床力学性能的影响规律，本文设计了三种级配进行研究，三种级配的过筛百分比曲线，如图 7所示。

图7 不同的道砟设计级配曲线Fig.7 Curves of different ballast gradation

图7中，级配曲线一所代表的是符合我国行业标准要求的最窄级配曲线，其粒径分布范围为31.5～50 mm。级配曲线二所代表的是符合我国行业标准中特级道砟级配要求的最宽级配曲线，其粒径分布范围为22.4～63 mm。在特级级配提出之前，我国主要采用级配范围较宽的一级级配对道砟材料的级配进行控制。基于此，本文还对颗粒粒径在13～75 mm范围内分布的宽级配道砟集料进行了分析。

本文对高速以及重载情况下三种不同级配范围的道砟集料进行了循环荷载道砟箱数值试验，并记录了在循环荷载2 000次情况下轨枕的沉降规律。

图 8出示了轨枕垂向位移随循环荷载变化的时程曲线，由稳定后轨枕位移的放大图可以看出，在循环荷载作用下，轨枕的沉降主要由两部分组成，一部分是由于道砟间的咬合特性所产生的弹性变形，该部分变形可在卸载的过程中完全恢复，另一部分是在循环荷载作用下所产生的残余变形，尽管这部分变形相对于弹性变形在每次荷载中所占的比例都很小，但该部分变形在轨枕卸载后却无法恢复。

由于轨枕沉降曲线存在弹性行程，为便于图示，本文将不同级配道砟集料每个荷载周期轨枕位移起始点位置随荷载次数的变化规律列于图 9、图 10。

图8 轨枕沉降曲线及位移放大图Fig.8 Settlement curve of sleeper and megascopic results

图9 高速运营条件下轨枕的沉降规律Fig.9 Sleeper settlement curve of high-speed railway

图10 重载运营条件下轨枕的沉降规律Fig.10 Sleeper settlement curve of heavy-haul railway

由图 9、可以看出，在高速的运营条件下级配一、二所代表的宽级配道砟颗粒所产生的累计沉降较小，而窄级配的道砟集料产生了较大的沉降量。由图 10可以看出，在重载情况下，道砟级配对道床沉降的影响规律截然不同，级配范围较窄的道床所产生的沉降量较小。

3 不同运营条件下细观动力特性分析

图11给出了不同运营情况下一个周期内轨枕的平均弹性位移幅值。

图12给出了道砟的切向摩擦运动速度随循环荷载作用次数变化的曲线图，道砟颗粒的平均切向运动速度定义如下式：

图11 不同运营条件下轨枕平均弹性位移幅值Fig.11 Elastic displacement amplitude of Sleeper in different operating condition

(5)

式中:Vt为道砟的平均切向摩擦速度;M为道砟集料中发生接触的总数;n为总接触中发生相对摩擦运动的接触数;vi为第i组两枚发生接触的道砟沿接触面的摩擦运动速度。由于在加载和卸载过程中，道砟颗粒的摩擦运动速度会呈现明显的周期性变化，为图示清晰，本文选取了道砟颗粒的平均切向摩擦运动速度进行分析，并将不同运营条件及级配情况下道砟颗粒的平均切向摩擦速度比较结果，示于图 13。

图12 道砟平均切向速度随荷载作用变化曲线Fig.12 Curve of ballast mean shear velocity changing with cycling number

结合图 11及图 13可以看出，在重载铁路大轴重的荷载形式作用下，有砟道床达到其弹性变形极限后进入塑性变形阶段，由颗粒间的切向相对错动而引起残余变形。且较窄级配的道砟级集料具有较大的弹性，这与图 13所示当道砟颗粒发生相对滑动时，窄级配的道砟集料因具有较大的摩阻力而导致了较小的相对切向摩擦运动速度的结果相吻合，这也是重载运营条件下窄级配道砟颗粒产生较小的累积沉降的原因。

对比高速情况下的不同级配道床的弹性位移以及相对切向运动速度可以发现，不同级配的道床在高速运行条件下，其弹性变性范围并无明显区别，且小于重载运营条件下的弹性变形，这说明在高速运营条件下列车低轴重、高频率的荷载特点并未达到散体道床的弹性极限，结合图 13中高速运营条件下道床平均切向速度的结果可以发现，与重载线路不同，高速条件下颗粒间的相互错动并非是有砟道床产生沉降的唯一原因。

图13 不同工况下道砟平均切向运动速度对比Fig.13 Comparison of ballast mean shear velocity in different operating condition

为明晰高速条件下有砟道床累计沉降的产生机理，本文对高速运营条件下有砟道床的各项动力指标进行了深入研究。研究发现，在高速铁路高频荷载作用下，道砟颗粒除会发生相互错动之外，相比于重载线路，还会发生较大的旋转，现定义道砟颗粒每个时步的平均旋转角速度如下：

(6)

式中：ωs为道砟颗粒的平均旋转角速度；N为道砟颗粒总数；ωt2为当前时步道砟颗粒质心的角速度矢量；ωt1为上一时步道砟颗粒质心的角速度矢量。道砟平均转动角速度随荷载作用次数的变化曲线，如图 14所示。

图14 道砟颗粒平均旋转角速度Fig.14 Mean angular velocity of ballast particles

由图 14可以看出在高速运营条件下，有砟道床的颗粒的平均角速度明显大于重载线路，且窄级配的道砟集料在高速运营条件下所产生的平均旋转角速度较大。这主要是由于宽级配的道砟集料由于小粒径颗粒对道床孔隙具有填充效应，使得宽级配道床更为密实，从而限制了道砟的自由旋转，这也是宽级配道砟集料在高速运营条件下所产生较小沉降量的一方面原因。文献[21]中三轴试验的结果佐证了这一结论。

4 结 论

本文提出了一套基于三维激光扫描技术对真实道砟颗粒外形进行精细化模拟的方法，并以此为基础，建立了循环荷载作用下的道砟箱体数值模型，基于验证后的模型，研究了不同道砟级配的散体道床在不同线路条件下的沉降力学特性，得到的主要结论如下：

(1) 本文所提出的三维激光扫描还原方法及离散元颗粒填充算法能实现道砟颗粒复杂外形的精确模拟，基于该套方法所建立的离散元模型能较好的模拟散体道床的真实情况。

(2) 散体道床累计沉降大致可分为两个阶段，即初期沉降阶段及稳定沉降阶段，在初期沉降阶段中，初始数十次循环荷载所产生的道床残余变形量最大，随着荷载次数的增多，道床发生进一步密实，每个周期所产生的道床残余变形量逐渐减小。当达到一定荷载次数后，道床进入稳定沉降阶段，即每次荷载所产生的道床的残余变形量基本不变。道床沉降随荷载作用次数基本成线性关系。

(3) 针对于新建或捣固后的散体道床，不同线路条件下，引起道床沉降的原因有所不同。道砟颗粒间的相互错动是引发重载铁路道床沉降主要原因。而对于高速铁路，其沉降则是由高频荷载作用下颗粒的转动及相互错动所构成的复合运动所引发。

(4) 由于线路的运营条件不同，不同级配散体道床的力学性能也不相同，应针对不同的线路条件，提出不同的道砟级配曲线要求，这一点建议在相关行业规范中予以考虑。

[1] ANDERSON W F, FAIR P.Behavior of railroad ballast under monotonic and cyclic loading[J].Journal of Geotechnical and Geoenvironmental Engineering, 2008, 134(3): 316-327.

[2] 胡仁伟, 王红, 赵国堂, 道碴动三轴试验研究[J].中国铁道科学, 2001,22(2): 104-109.

HU Renwei, WANG Hong, ZHAO Guotang, Study on dynamic triaxial test and accumulated deformation of ballast[J].China Railway Science, 2001, 22(2): 104-109.

[3] 王红.道碴弹性和累积变形的试验研究[J].中国铁道科学, 2001, 22(6): 106-110.

WANG Hong.Test and study on ballast elasticity and accumulated deformation[J].China Railway Science, 2001, 22(6): 106-110.

[4] INDRARATNA B, TENNAKOON N, NIMBALKAR S, et al.Behaviour of clay-fouled ballast under drained triaxial testing[J].Geotechnique, 2013, 63(5): 410-419.

[5] AL-SAOUDI N K S, HASSAN K H.Behaviour of track ballast under repeated lloading[J].Geotechnical and Geological Engineering, 2014, 32(1): 167-178.

[6] LIM W L.Mechanics of railway ballast behaviour[D].Notlingham: University of Nottingham, 2004.

[7] LIM W L, MCDOWELL G R.Discrete element modelling of railway ballast[J].Granular Matter, 2005, 7(1): 19-29.

[8] LU M, MCDOWELL G R.The importance of modelling ballast particle shape in the discrete element method[J].Granular Matter, 2006, 9(1/2): 69-80.

[9] 赵金凤,严颖，季顺迎.基于离散元模型的土石混合体直剪试验分析[J].固体力学学报，2014(2):124-134.

ZHAO Jingfeng, YAN Ying, JI Shunying.Analysis of direct shear test of soil-rock mixture based on discrete element model[J].Chinese Journal of Solid Mechanics,2014(2):124-134.

[10] 季顺迎，苏勇，严颖.含沙铁路道碴弹性模量和沉降量的试验研究[J].铁道科学与工程学报, 2011, 8(2): 47-52.

JI Shunying, SU Yong, YAN Ying.Experimental studies on elastic modulus and settlement of railway ballast with sand[J].Journal of Railway Science and Engineering, 2011, 8(2): 47-52.

[11] 边学成,李公羽,李伟,等.基于颗粒真实几何形状的铁路道砟剪切过程三维离散元分析[J].工程力学, 2015,32(5): 64-75.

BIAN Xuecheng, LI Gongyu, LI Wei.Railway ballast’s shape process based on particles’ real geometry[J].Engineering Mechanics, 2015, 32(5): 64-75.

[12] HUANG H, SHEN S, TUTUMLUER E.Sandwich model to evaluate railroad asphalt trackbed performance under moving lLoads[J].Transportation Research Record: Journal of the Transportation Research Board, 2009, 2117(1): 57-65.

[13] HUANG H, TUTUMLUER E, DOMBROW W.Laboratory characterization of fouled railroad ballast behavior[J].Transportation Research Record: Journal of the Transportation Research Board, 2009, 2117(1): 93-101.

[14] INDRARATNA B, THAKUR P K, VINOD J S.Experimental and numerical study of railway ballast behavior under cyclic loading[J].International Journal of Geomechanics, 2010, 10(4): 136-144.

[15] 章志勇.三维模型几何相似性比较的研究[D].杭州：浙江大学，2005.

[16] FORBES K, NICOLLS F, JAGER G D, et al.Shape-from-silhouette with two mirrors and an uncalibrated camera[J].Lecture Notes in Computer Science, 2006, 3952: 165-178.

[17] INDRARATNA B., NGO N T.Behavior of fresh and fouled railway ballast subjected to direct shear testing: discrete element simulation[J].International Journal of Geomechanics, 2014, 14(1): 34-44.

[18] 徐旸,高亮,杨国涛，等.道砟颗粒的精细化建模及对道床力学性能影响[J].铁道学报,2014,36(9): 73-78.

XU Yang, GAO Liang, YANG Guotao, et al.Fine modelling of ballast grains and influence on mechanical properties of track bed[J] Journal of the China Railway Society,2014,36(9): 73-78.

[19] 徐旸，高亮，井国庆，等.脏污对道床剪切性能影响及评估指标的离散元分析[J].工程力学, 2015, 32(8): 96-102.

XU Yang, GAO Liang, JING Guoqing, et al.Shear behavior analysis of fouled railroad ballast by DEM and its evaluation index[J].Engineering Mechanics, 2015, 32(8): 96-102.

[20] 中华人民共和国铁道行业标准.铁路碎石道砟:TB/T2140—2008[S]．北京：中国铁道出版社，2008.

[21] INDRARATNA B, KHABBAZ M H, SALIM W, et al.Ballast characteristics and the effects of geosynthetics on rail track deformation[C] Int Conference on Geosyntbetics and Geoenvironmental Engineering Mumbai India, 2004: 3-12.

Influences of ballast gradation on railway ballast bed dynamic characteristics Based on Laser Scanning and Discrete Element Method

XU Yang1,2, GAO Liang1,2, CAI Xiaopei1,2, HOU Bowen1,2, ZHAO Yunzhe1,2

(1.College of Civil Engineering, Beijing Jiaotong University，Beijing 100044，China;2.Beijing Engineering and Technology Research Center of Rail Transit Line Safety and Disaster Prevention，Beijing 100044，China)

Ballast gradation has obviously an influence on ballast bad’s dynamic performances.The three-dimensional laser scanning technique was used to capture and analyze shape features of ballasts bere.Based on the reconstructed results of ballast shape, a construction method of ballast discrete element model was proposed.Then, a ballast box numerical model with cyclic loading was established.The influence laws of ballast gradation on ballast bed dynamic settlement under high-speed and heavy-haul railway conditions were studied with the numerical model, the microscopic ballast bed settlement mechanism was analyzed as well.The results showed that the railway ballast bed has different degradation mechanisms under different operation conditions, the relative motion between ballasts is the main reason for the settlement of heavy-haul railway ballast bed; for high-speed railway, the settlement of ballast bed is influenced by the rotation of ballast particles as well.Thus, it was suggested that different railway conditions should adopt different ballast gradation curves in the design code.

railway ballast bed; ballast gradation; discrete element method; ballast bed degradation; dynamic response

国家自然科学基金重点项目(U1234211);国家自然科学基金面上项目(51578053;51578055);中央高校基本科研业务费(C15RC00120);北京市科技新星计划(XX2013012)

2016-05-17 修改稿收到日期：2016-07-13

徐 旸 博士生，1989年生

高 亮 博士，教授，1968年生

U213.7

A

10.13465/j.cnki.jvs.2017.05.020