径向动静压浮环轴承-转子系统稳定性分析

郭 红，夏伯乾，孙一休

(郑州大学 机械工程学院，郑州 450001)

径向动静压浮环轴承-转子系统稳定性分析

郭 红，夏伯乾，孙一休

(郑州大学 机械工程学院，郑州 450001)

以径向动静压浮环轴承-转子系统为研究对象，计入浮环质量和转子刚度建立了统一的动力学方程，用Routh-Hurwitz准则推导了单质量弹性对称系统的稳定性判据。用有限差分计算了某高速径向动静压浮环轴承的刚度系数和阻尼系数，在此基础上得到了不同浮环质量和转子刚度下动静压浮环轴承-转子系统的稳定性曲线。计算结果表明，浮环质量对系统稳定性影响不大，而随着转子刚度减小，系统失稳转速迅速降低。该文在高速浮环轴承-弹性转子稳定性整体建模和分析方面有较大的参考意义。

径向浮环轴承；转子刚度；浮环质量；失稳转速

动静压浮环轴承综合了动压、静压和浮环轴承的优点，具有启动摩擦小、承载力大、稳定性好的特点，在燃气轮机、涡轮增压器等高速旋转机械上应用广泛。国内外很多学者对不同结构形式的滑动轴承油膜特性及应用进行了广泛研究[1-4]，而对于浮环轴承，沈那伟等[5]探讨了微型燃气轮机浮环轴承动力学参数的影响因素；WANG等[6]采用数值方法分析了气体浮环轴承的混沌和次谐运动；WANG等[7]讨论了制造公差对透平机浮环轴承动态特性的影响；KOUTSOVASILIS等[8]以浮环轴承支承的透平转子为研究对象，分析了油膜引起的次同步振动；SAN ANDRES等[9]考虑了温度对浮环轴承性能的影响；郭红等[10-12]以径向浮环轴承为研究对象，针对浮环和转子建立统一的动力学方程，研究了系统的稳定性及浮环轴承多稳定区域。本文以径向动静压浮环轴承-转子系统为研究对象，计入浮环质量和转子刚度建立轴颈和浮环统一的动力学方程，利用Routh-Hurwitz准则推导系统的稳定性判据，分析不同转速和偏心率下浮环质量和转子刚度对系统稳定性的影响。

1 径向浮环动静压轴承控制方程

1.1 控制方程

图1为径向动静压浮环轴承内外膜结构示意图，内膜在浮环内侧设置4个深浅腔，外膜在轴瓦内侧设置5个深浅腔，每个深腔中央开设进油孔。

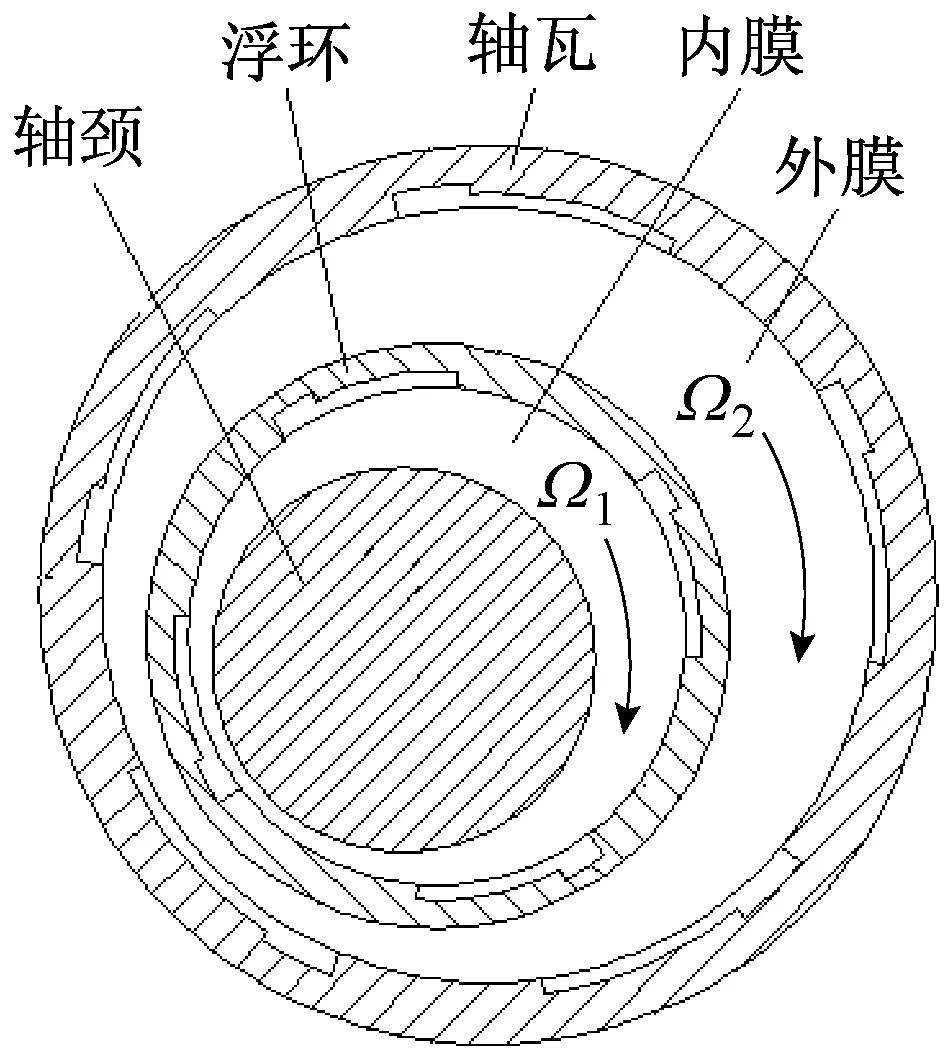
图1 动静压浮环轴承结构Fig.1 Inner and outer film structure of floating ring bearing

用φ表示圆周方向坐标，λ表示轴向坐标。取无量纲因子

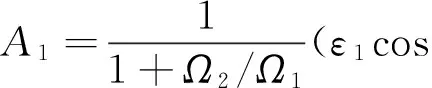
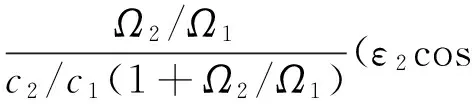
A2=(ε2cosφ2+ε02θ2sinφ2)

可得到支配内外层油膜的无量纲Reynolds方程：

(1)

1.2 边界条件

具有深浅腔的动静压轴承存在压力边界条件和深腔流量平衡条件，如图2所示。

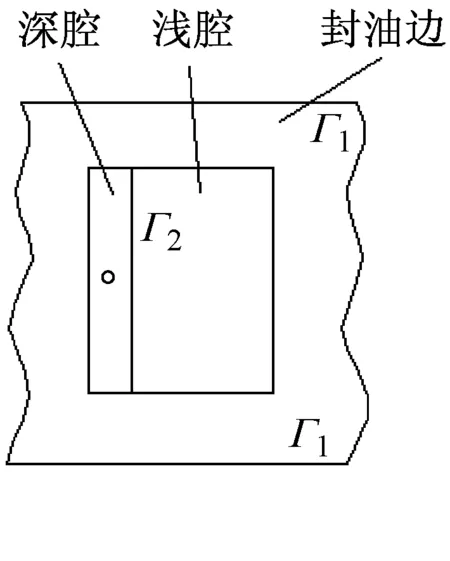
压力边界条件：

(2)

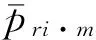
无量纲流量平衡条件：

(3)

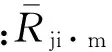
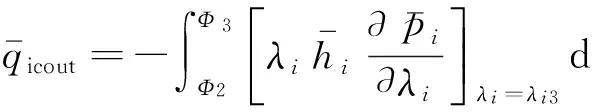
无量纲油膜厚度：

(4)

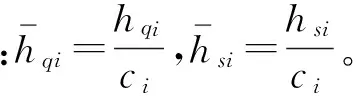
1.3 浮环平衡工作条件

当内外膜作用到浮环上的力和力矩相等时，浮环即可保持平衡运转。

(5)

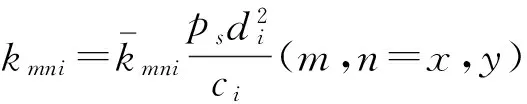
2 计入浮环质量和转子刚度稳定性分析

如图3所示，单质量弹性对称转子系统由一对浮环轴承支承。设转子质量2m1，轴弯曲刚度为2k；单个浮环质量为m2。轴颈的简谐变动位移为x1,y1，内层油膜作用力为Fx1,Fy1；浮环的简谐变动位移x2,y2，外层油膜作用力为Fx2,Fy2；轴颈中心的静平衡位置为(x10,y10)，受扰动后某时刻轴颈中心为(x1,y1)，圆盘中心相对轴颈中心扰动位移为(ξ,η)。

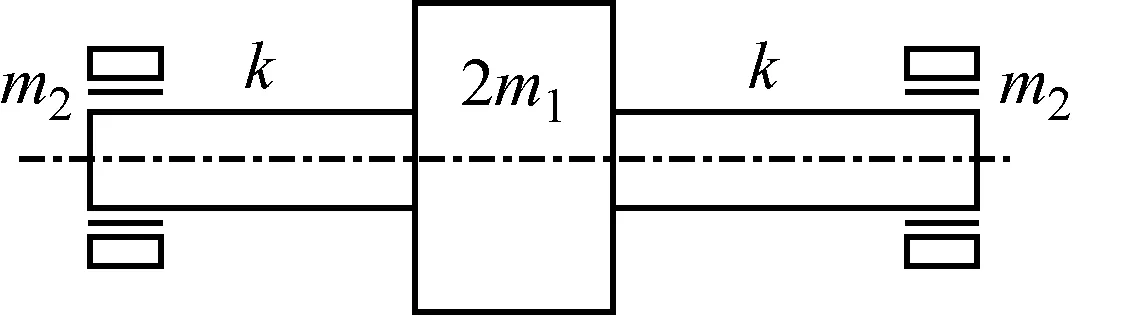
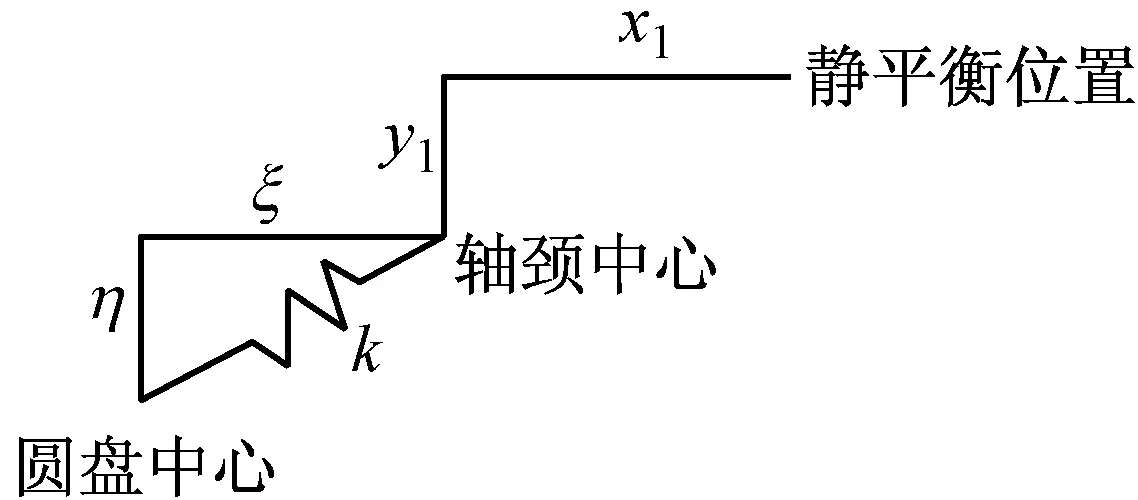
图3 浮环轴承内外膜动力学模型Fig.3 Dynamics model of floating ring bearing

圆盘动力学方程为

(6)

其中：

浮环动力学方程：

(7)

令ξ=ξ0evt，η=η0evt，联立方程(6)、(7)得到：

(8)

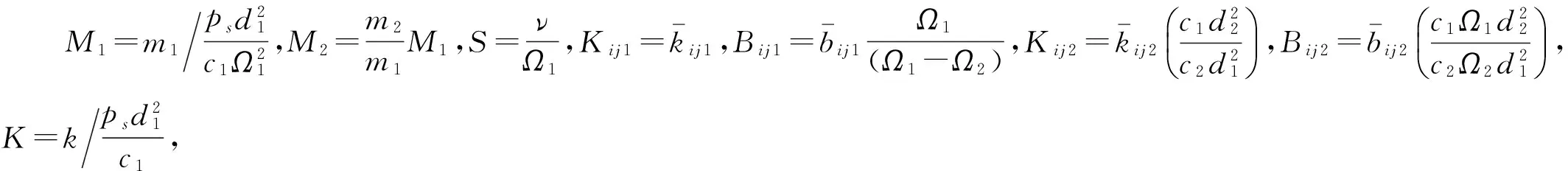
(9)

令系数矩阵行列式为零，可得到特征方程：

α0S10+α1S9+α2S8+α3S7+α4S6+α5S5+

α6S4+α7S3+α8S2+α9S+α10=0

(10)

式中：各项系数分别为

α7=K2(B2G1+B1G2)+K2M1[(Bxx2+Byy2)K1+ (Bxx1+Byy1)K2+(Kxx2+Kyy2)G1+(Kxx1+Kyy1)G2]+K2M2[(Bxx2+Byy2)K1+(Kxx2+Kyy2)G1]+2KM1(G1K2+G2K1)

α8=K2(K2B1+B2K1+G1G2)+K2M1[(Kxx2+Kyy2)K1+(Kxx1+Kyy1)K2]+K2M2(Kxx2+Kyy2)K1+2KM1K1K2

α9=K2(G1K2+G2K1)

α10=K2K1K2

式中：

G1=Bxx1Kyy1+Byy1Kxx1-Bxy1Kyx1-Byx1Kxy1

G2=Bxx2Kyy2+Byy2Kxx2-Bxy2Kyx2-Byx2Kxy2

G=Bxx1Kyy2+Bxx2Kyy1-Bxy1Kyx2-Bxy2Kyx1-Byx1Kxy2-Byx2Kxy1+Byy1Kxx2+Byy2Kxx1Ks=(Kxx1+Kxx2)(Kyy1+Kyy2)-(Kxy1+Kxy2)(Kyx1+Kyx2)

Bs=(Bxx1+Bxx2)(Byy1+Byy2)-(Bxy1+Bxy2)(Byx1+Byx2)

B1=Bxx1Byy1-Bxy1Byx1

B2=Bxx2Byy2-Bxy2Byx2

K1=Kxx1Kyy1-Kxy1Kyx1

K2=Kxx2Kyy2-Kxy2Kyx2

按照Routh-Hurwitz准则，可得到计入浮环质量和转子刚度的动静压浮环轴承-转子系统稳定性条件：

(11)

式中

当浮环轴承结构参数和工作条件确定时，求出内、外膜的刚度系数和阻尼系数，即可按照上述稳定性条件判断系统是否处于稳定状态，计算时采用递归法求解矩阵。

3 计入浮环质量和转子刚度稳定性算例

图1所示向心浮环动静压轴承结构参数如表1所示。取润滑油动力黏度μ=4.475×10-3Pa·s，供油压力ps=1.0 MPa，转子质量2m1=3.5 kg，浮环质量m2=0.06 kg，转子刚度k=1.3×105N/m。

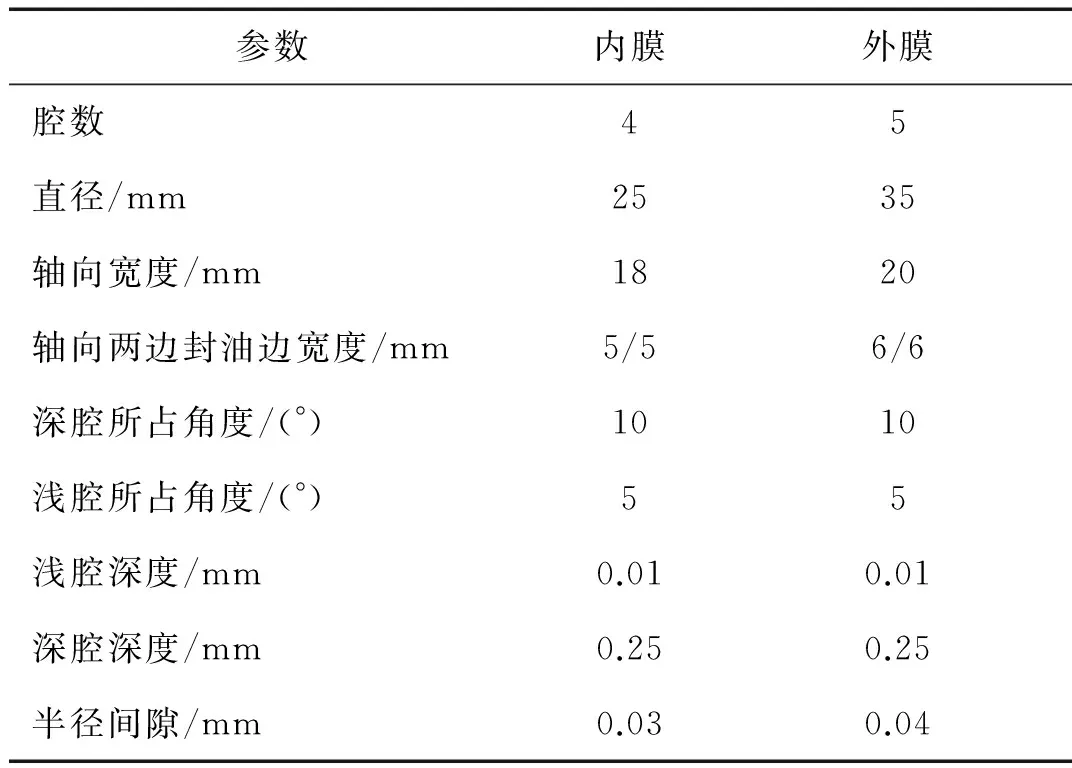
表1 圆柱浮环动静压轴承结构参数Tab.1 Parameters of journal floating ring hybrid bearing

计算时给定外膜偏心率，在一定主轴转速下通过迭代保证浮环平衡，然后计算动特性参数，按式(11)判断系统的稳定性。以一定的步长增加转速，重复上述过程。

3.1 转子刚度对失稳转速的影响

图4为浮环质量为0.06 kg时，不同转子刚度下系统失稳转速随偏心率的变化规律。可以看出，同样偏心率下，刚性转子系统的失稳转速最高，弹性转子系统的失稳转速随转子刚度增加而提高，但不会超过刚性转子。另一方面，系统失稳转速随偏心率增加而提高，且转子刚度越大，提高幅度越大。反映出当转子刚度大时，轴承油膜是影响系统稳定性的主要因素，而在转子刚度小时(例如k=0.3 MN/m)，转子成为影响失稳转速的主要因素。因此，增大转子刚度(减小变形挠度)可以提高系统的稳定性。

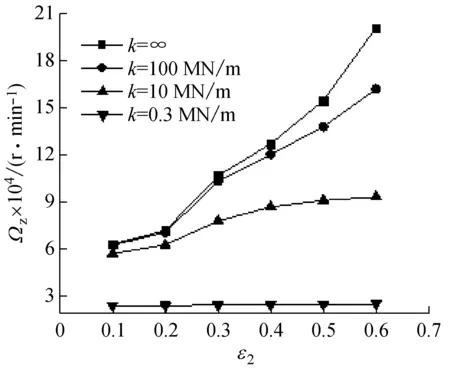
图4 不同刚度下系统失稳转速Fig.4 Variation of threshold speed with rotor rigidity

3.2 浮环质量对失稳转速的影响

图5为刚性对称转子系统不同偏心率下失稳转速随浮环质量的变化规律。可以看出，浮环质量一定时，系统失稳转速随偏心率增大而迅速提高；同一偏心率下，随着浮环质量由0(不考虑)增加到0.10 kg，系统失稳转速逐渐下降，但幅度非常有限。

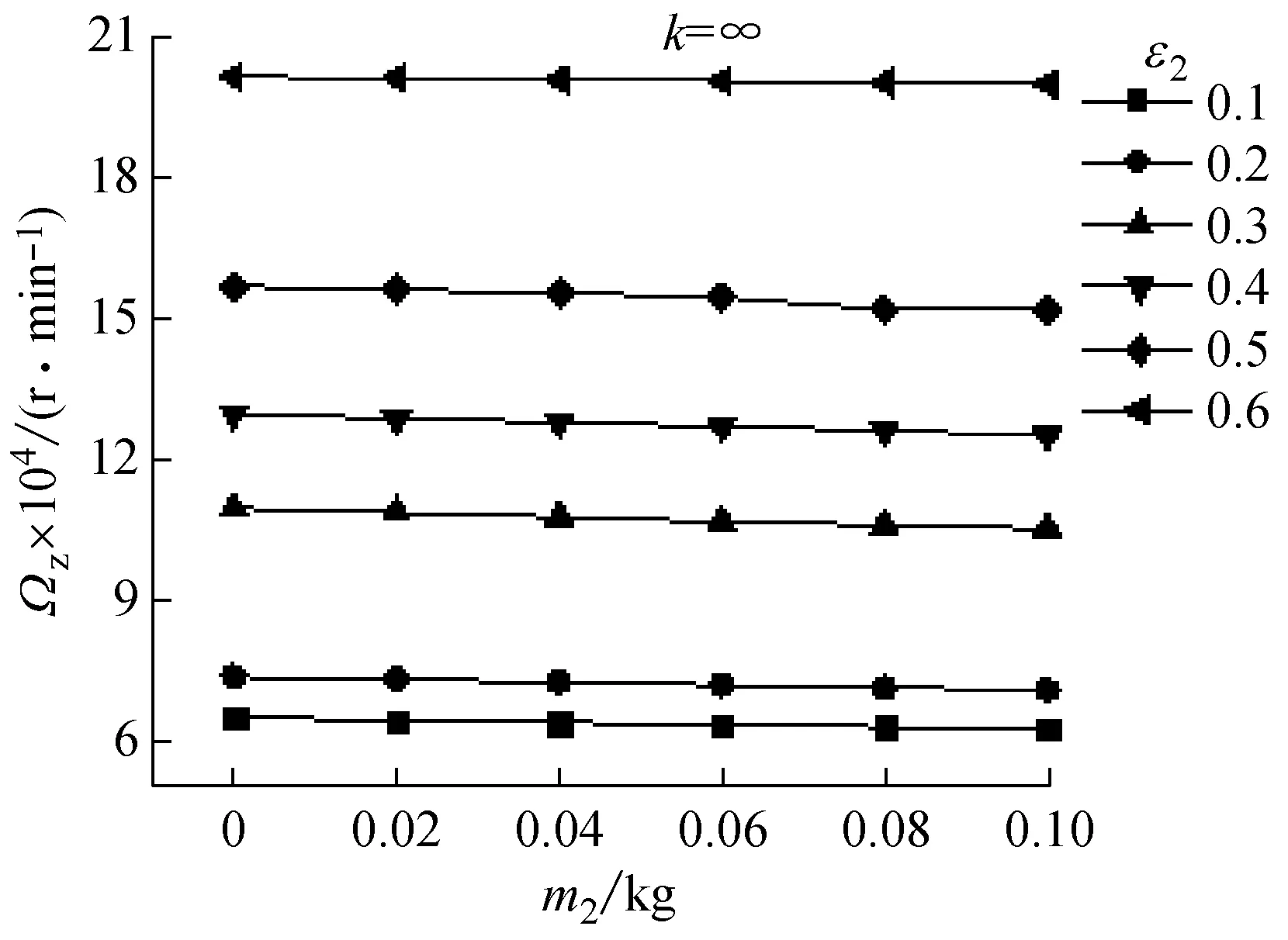
图5 刚性转子系统失稳转速Fig.5 Variation of threshold speed (k=∞)

图6为弹性对称转子系统不同偏心率下失稳转速随浮环质量的变化规律。转子刚度取为k=10 MN/m，可以看出，浮环质量一定时，系统失稳转速随偏心率增大而迅速提高；同一偏心率下，随着浮环质量由0(不考虑)增加到0.10 kg，系统失稳转速逐渐下降，但幅度不大。比较图5和图6，可以看出同样条件下弹性转子失稳转速低于刚性转子。

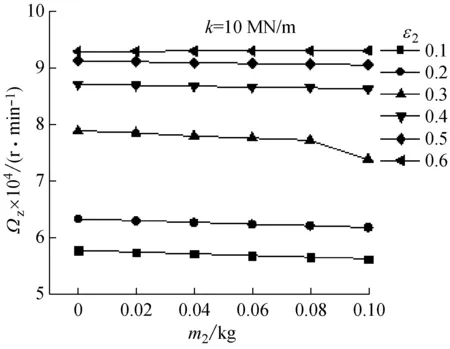
图6 弹性转子系统失稳转速Fig.6 Variation of threshold speed (k=10 MN/m)

3.3 转子刚度和浮环质量对失稳转速的综合影响

图7为不同转子刚度下，系统失稳转速随浮环质量的变化规律。取外膜偏心率为0.3，可以看出，浮环质量相同时，系统失稳转速随转子刚度的增加而迅速提高；另一方面，各刚度下系统失稳转速随浮环质量的增加略有下降，且转子刚度越大下降越明显，转子刚度小时(k=0.3 MN/m)，浮环质量对系统失稳转速基本没有影响。

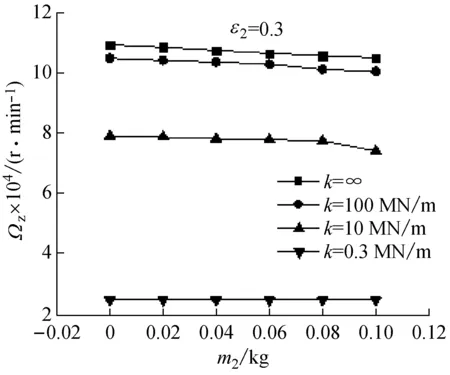
图7 不同浮环质量和刚度下的失稳转速Fig.7 Variation of threshold speed with floating ring mass and rotor stiffness

4 结 论

(1) 考虑转子刚度和浮环质量，建立动静压浮环轴承-弹性转子系统的动力学方程，在此基础上给出了单质量对称转子系统的稳定性判据。

(2) 系统失稳转速随偏心率增加而提高，且转子刚度越大，提高幅度越大。同样偏心率下，刚性转子系统的失稳转速最高，弹性转子系统的失稳转速随转子刚度增加而提高。

(3) 浮环质量一定时，系统失稳转速随偏心率增大而迅速提高；同一偏心率下，随着浮环质量增加，系统失稳转速逐渐下降，但幅度很小。

[1] 马辉, 李辉, 牛和强, 等.滑动轴承-转子系统油膜失稳参数影响分析[J].振动与冲击, 2013, 32(23): 100-104.

MA Hui, LI Hui, NIU Heqiang, et al.Parametric influence analysis of oil-film instability in a sliding bearing-rotor system[J].Journal of Vibration and Shock, 2013, 32(23): 100-104.

[2] GUO Hong, LAI Xinmin, CEN Shaoqi.Theoretical and experimental study on dynamic coefficients and stability for a hydrostatic/hydrodynamic conical bearing[J].ASME, Journal of Tribology, 2009, 131(4): 041701-041707.

[3] BROUWER M D, SADEGHI F, LANCASTER C, et al.Whirl and friction characteristics of high speed floating ring and ball bearing turbochargers[J].Journal of Tribology, 2013, 135(10): 1-9.

[4] ZHOU Hailun, FENG Guoquan, LUO Guihuo, et al.The dynamic characteristics of a rotor supported on ball bearings with different floating ring squeeze film dampers[J].Mechanism and Machine Theory, 2014, 80: 200-213.

[5] 沈那伟, 焦映厚, 陈照波, 等.微型燃气轮机浮环轴承动力学参数影响因素研究[J].振动工程学报, 2012, 25(6): 714-723.

SHEN Nawei, JIAO Yinghou, CHEN Zhaobo, et al.Study of impact factor on dynamic parameters of the floating ring bearing for micro gas turbogenerator[J].Journal of Vibration Engineering, 2012, 25(6): 714-723.

[6] WANG C C, YAU H T, WANG C C.Chaotic and subharmonic motion analysis of floating ring gas bearing system by hybrid numerical method[J].Mathematical Problems in Engineering, 2013: 1-14.

[7] WANG Longkai, BIN Guangfu, LI Xuejun, et al.Effects of floating ring bearing manufacturing tolerance clearance on the dynamic characteristics for turbocharger[J].Chinese Journal of Mechanical Engineering, 2015, 28(3): 530-540.

[8] KOUTSOVASILIS P, DRIOT N, LU D, et al.Quantification of sub-synchronous vibrations for turbocharger rotors with full-floating ring bearings[J].Archive of Applied Mechanics, 2015, 85(4): 481-502.

[9] SAN ANDRES L, BARBARIE V, BHATTACHARYA A, et al.On the effect of thermal energy transport to the performance of (semi) floating ring bearing systems for automotive turbochargers[J].Journal of Engineering for Gas Turbines and Power, 2012, 134: 1-10.

[10] 郭红, 张直明, 岑少起, 等.径向浮环动静压轴承稳定性研究[J].振动与冲击, 2012, 31(17): 17-21.

GUO Hong, ZHANG Zhiming, CEN Shaoqi, et al.Stability of journal floating ring hybrid bearing[J].Journal of Vibration and Shock, 2012, 31(17): 17-21.

[11] 孙一休, 郭红, 张绍林, 等.计入浮环质量的浮环动静压轴承稳定性分析[J].润滑与密封, 2015, 40(5): 47-51.

SUN Yixiu, GUO Hong, ZHANG Shaolin, et al.Stability analysis of floating ring hybrid bearing considering floating ring mass[J].Lubrication Engineering, 2015, 40(5): 47-51.

[12] 郭红, 张直明, 张绍林, 等.径向动压浮环轴承-转子系统多稳定区域研究[J].振动与冲击, 2016, 35(2): 168-172.

GUO Hong, ZHANG Zhiming, ZHANG Shaolin, et al.Multi stable regions of hydrodynamic floating ring journal bearing-rotor system[J].Journal of Vibration and Shock, 2016, 35(2): 168-172.

Stability analysis of a journal floating ring hybrid bearing-rotor system

GUO Hong, XIA Boqian, SUN Yixiu

(School of Mechanical Engineering, Zhengzhou University, Zhengzhou 450001, China)

A unitized dynamic model for a journal floating ring hybrid bearing-rotor system was established considering floating ring mass and rotor stiffness.The stability criterion for the journal floating ring hybrid bearing-rotor system was derived using Routh-Hurwitz method.The dynamic characteristic coefficients of inner and outer films for a high speed floating ring bearing were calculated with the finite difference method under different operation conditions.Further more the variation of the threshold rotating speed of the bearing-rotor system with floating ring mass and rotor stiffness was acquired.The results showed that the threshold rotating speed of the bearing-rotor system decreases slightly with increase in floating ring mass under different eccentricities; at the same time, the threshold rotating speed of the bearing-rotor system increases quickly with increase in rotor stiffness.The results provided a reference for the overall modeling and stability analysis of floating ring hybrid bearing-elastic rotor systems.

journal floating ring bearing; rotor stiffness; floating ring mass; threshold rotating speed

国家自然科学基金资助项目(51575498)

2015-12-07 修改稿收到日期：2016-02-18

郭红 女，博士，教授，1970年9月生

TH133.3

A

10.13465/j.cnki.jvs.2017.05.002