共振频率可调式非线性压电振动能量收集器

吴义鹏，季宏丽，裘进浩，张 浩

(南京航空航天大学 航空宇航学院机械结构力学及控制国家重点实验室，南京 210016)

共振频率可调式非线性压电振动能量收集器

吴义鹏，季宏丽，裘进浩，张 浩

(南京航空航天大学 航空宇航学院机械结构力学及控制国家重点实验室，南京 210016)

振动能量回收技术能够将环境中的机械振动能转换成电能，进而为微功耗装置供电，具有良好的应用前景。设计了一种利用压电材料的新型振动能量收集器，该机电耦合结构由一对非对称压电悬臂梁组成，悬臂梁末端固定有永磁体，利用永磁体产生的非线性力，实现了悬臂梁共振频率与外界激振频率的匹配调节。提出了该结构的理论模型，借助Matlab/Simulink数值分析软件对理论模型进行了仿真分析，并通过实验进行了验证。实验结果表明外界激励加速度幅值为3 m/s2的时，结构即能实现较大频带范围内的频率匹配调节，频带范围不低于6.5 Hz，最大回收功率不低于2 mW。

能量回收；频率匹配；压电；非线性

无线传感器节点作为典型的智能传感器，能够直接感受客观世界的物理信息，成了物联网底层网络的重要组成部分。随着当今科技的迅猛发展，无线传感器节点在所需成本越来越低的情况下，智能化及可靠性程度却越来越高。然而绝大多数节点目前仍使用电池供电技术，如果传感器网络中的节点数量巨大，又或者节点布置在危险区域、复杂结构内部，一旦电池电量耗尽，更换电池将需要庞大的维护费用，甚至会因为无法更换而影响节点使用寿命。

基于上述原因，回收自然环境中太阳能、风能、振动能等能量源，并将其转化成电能的微发电技术有着相当重要的应用价值。其中机械振动能几乎处处存在，同时具有相当可观的能量密度，吸引了众多学者的关注[1-3]。压电材料由于具有较高的能量密度以及便于和结构集成等优点，利用正压电效应将机械能转换电能成为了振动能量回收的一种主要方式。

早期学者研究发现压电悬臂梁是一种结构简单且有效的振动能量回收结构，一旦外界激振频率与悬臂梁的共振频率匹配，高品质因子的悬臂梁结构能够有效地放大激励振幅，使压电元件产生正负交替的大幅应变，进而高效地输出电能[4]。另外，曾平等[5]研究过易于和传感器节点集成的圆盘式发电结构，胡洪平等[6]提出过低频螺旋状压电能量回收装置，阚君武等[7]提出过多振子串联的压电俘能器等线性压电能量回收结构，一般均具有固定的一阶共振频率，一旦外界激振频率偏离该共振频率，结构振幅将急剧降低。考虑到实际环境振动源的复杂性，上述能量回收结构的实际应用仍存在一定的困难。为此，共振频率可调式、阵列式、多模态式、分段线性式、非线性式等更加适应一般环境振动特征的压电能量回收结构逐渐被提了出来。其中共振频率可调式能量回收结构具有较高的机械品质因数和能量密度，适合大多数振动频率随机缓慢变化的振动源。

EICHHORN等[8]提出一种简单可靠的共振频率手动调节装置，在悬臂梁轴向施加可调节的载荷改变结构的等效刚度，进而实现悬臂梁共振频率与激振频率的匹配功能，但频率匹配过程中装置必须停止工作。PILLATSCH等[9]提出了一种质量块滑动式压电梁结构能够根据外界激振频率被动调节质量块的位置，进而改变梁结构的共振频率，获得较大的振幅，该装置不需要外界干预即能实现频率匹配的自适应调节功能，但质量块滑动响应慢，不太适应频率变化较快且频繁的环境振动源。ROUNDY等[10]利用压电驱动器实现了压电悬臂梁的共振频率主动自适应调节，频率匹配速度快，但该方法需要额外的控制系统和驱动功耗。

在马华安等[11]实验研究的基础上，本文提出了一种同样基于非线性磁力调节结构共振频率的新型机电耦合结构，首次建立了该结构的二自由度非线性动力学模型并进行了仿真研究和讨论，最后通过实验进行了相关验证。

1 压电能量收集器的理论建模

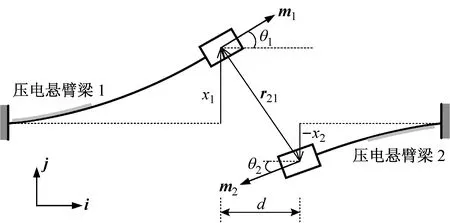
图1(a)所示为非线性压电能量收集器的原型结构示意图，结构由一对非对称压电悬臂梁组成：悬臂梁末端固定有永磁体质量块，永磁体之间产生互相排斥的非线性磁力；悬臂梁固定端与装置的基础框架相连。

(a)

(b)

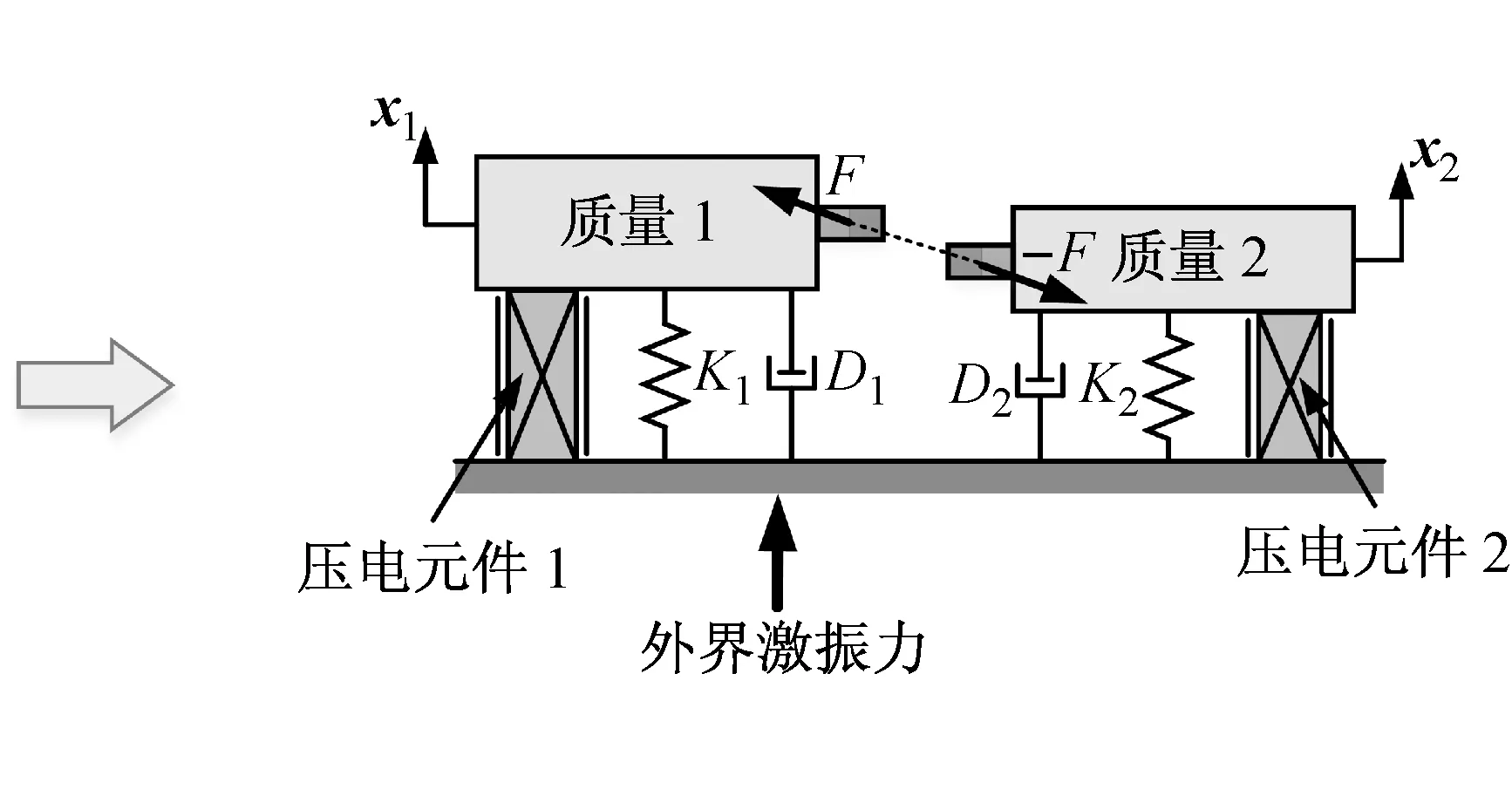
结构在外界振动源激励下，悬臂梁1和2发生受迫振动，振动位移分别记为x1和x2，由于非线性磁力的存在，x1和x2互相耦合却不线性相关。本文仅考虑悬臂梁1和2发生在一阶固有频率附近的振动，即振型为一阶模态振型，结合振动力学理论，该结构可以等效成二自由度非线性受迫振动系统。结构的等效模型如图1(b)所示，一对非对称悬臂梁分别等效成质量mi弹簧Ki阻尼Di(i= 1, 2)系统并集成有压电元件。环境振动源直接作用于系统基础框架上，非线性磁力作用于质量块mi上。

由于磁力的计算公式受永磁体形状、磁场分布等因素的影响十分复杂，为简化计算非线性磁力，结构中的永磁体将被近似看成磁矩分别为m1和m2的磁偶极子，结合文献[12]，可得简化后磁偶极子2作用在磁偶极子1上的作用力FB：

(1)

式中：μ0为真空磁导率；r为向量r21的模。建立图 1所示的直角坐标系，式(1)中各个向量可以写成如下形式：

m1=m1v1cosθ1i+m1v1cosθ1j

(2)

m2=-m2v2cosθ2i+m2v2cosθ2j

(3)

r21=-di+(x1-x2)j

(4)

式中：mi，vi分别为对应永磁体的磁化强度和体积，d为磁偶极子在i方向上的磁间距，磁偶极子与i方向的夹角θi可根据几何关系给出近似表达式：

(5)

(6)

根据文献[13]给出的结论，悬臂梁在振动过程中，j方向的磁力影响远远大于i方向的磁力影响，因此式(1)可作进一步简化，结合式(2)～(6)，忽略i方向上的向量分量，最终得到仅在j方向上的磁力FB，大小记为FB。对于给定的压电能量回收结构，磁力FB仅与悬臂梁的振动位移x1和x2有关，由于振动位移在mm级别，对FB在x1=0,x2=0处作二元泰勒展开，最终可得磁力的近似表达式，如下：

(7)

对于给定的机电耦合结构，式中a1，a2，b1，b2，c1，c2为常数，仅与悬臂梁梁长L1，L2和磁间距d有关。通过式(7)可知，一对悬臂梁必须是非对称设计，确保非线性磁力FB在理论上不恒等于0，且非对称性主要体现在悬臂梁的梁长上。假设磁偶极子2不发生振动，即x2=0，式(7)即等于众多文献在单自由度非线性动力学模型中简化的非线性磁力。

根据牛顿定律，式(8)给出了图1(b)中二自由度非线性系统的动力学方程[14]：

(8)

式中：Mi为系统等效质量；ξi为系统阻尼比；ωi为二自由度系统对应的共振频率；γ为外界激振加速度；αi为压电悬臂梁力电耦合因子；Vi为压电元件输出电压。根据压电效应方程，式(9)给出了压电机电耦合结构中的机械参数x1，x2和电学参数(I1，V1)，(I2，V2)之间的关系方程[14]。其中Ii，Ci分别为压电元件的输出电流和受夹电容。

(9)

2 压电能量回收结构的实验装置及参数

图2所示为实验系统结构示意图及压电能量回收结构实物图。振动能量回收实验系统基于dSPACE实时仿真控制器进行搭建，实时控制器数模转换端口输出正弦扫频激振信号，经功率放大器进入激振器输入端，使其产生相应频率的振动。装置框架上固定有加速度传感器，将实际激振加速度信号经信号调理仪反馈给实时仿真控制器，控制器计算加速度幅值并与设定的数值进行比较，进而让闭环系统实时调节输出增益，确保实际激振加速度幅值保持恒定。

非对称压电悬臂梁实物固定在有机玻璃制成的基础框架上，基础框架与水平放置的激振器相连，确保悬臂梁沿水平方向振动，抵消了质量块重力的影响。线性悬臂梁1和2以及末端质量块的材料均为不锈钢。为方便调节磁间距d，悬臂梁2可在基础框架上左右调节。

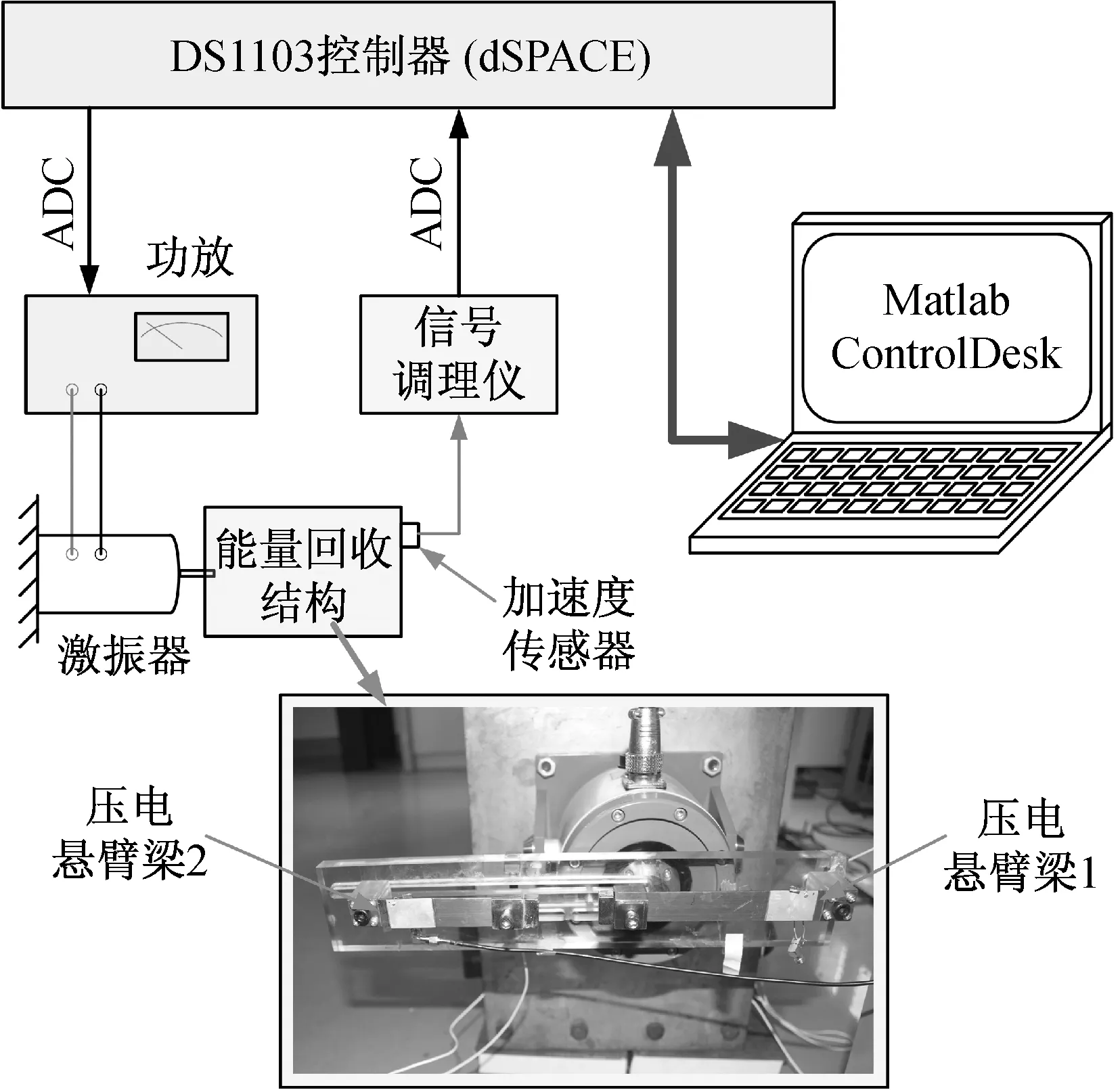
图2 实验系统结构示意图及压电能量回收结构实物图

Fig.2 The schematic of the experimental system and the photo of the piezoelectric energy harvesting structure

在上述闭环实验系统中首先测定线性条件下(结构中无磁力FB)，两个悬臂梁各自的结构参数，参照式(10)，最终实验测得压电悬臂梁结构的各项参数如表 1所示(永磁体的各项参数根据产品数据手册直接给出)，其中βi为压电悬臂梁开路输出电压与末端位移的比值，ωsi和ωoi分别为压电元件短路和开路条件下悬臂梁的共振角频率，Qi为结构的机械品质因子。

(10)

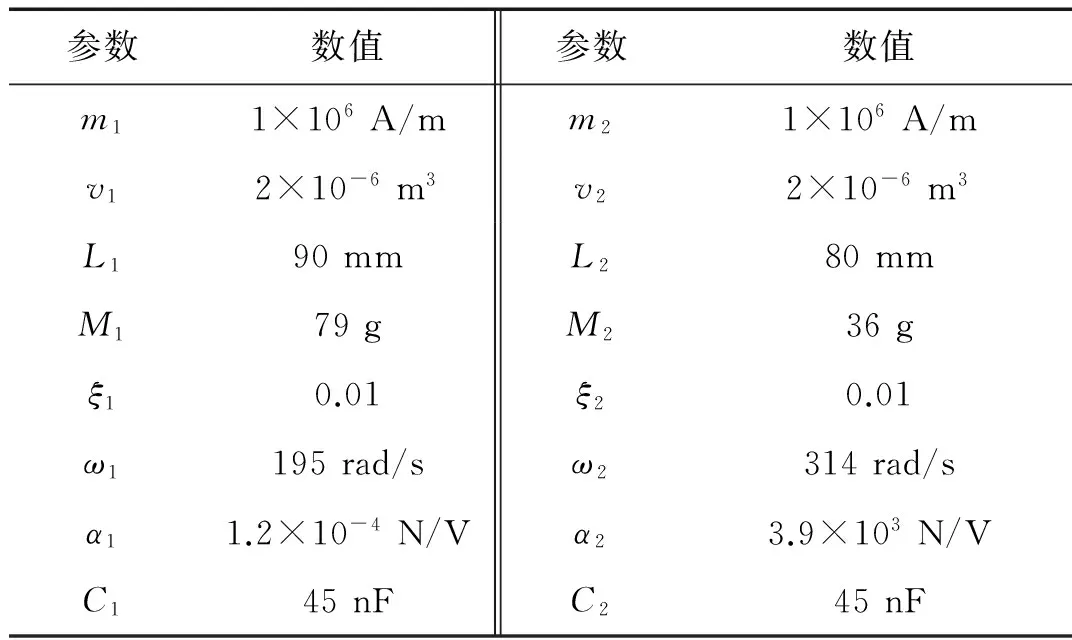
表1 二自由度非线性系统的相关参数Tab.1 Parameters of the two degree of freedom nonlinear system

3 压电能量收集器的仿真及实验研究

3.1 仿真结果及其讨论

式(8)和(9)分别给出了二自由度非线性系统动力学和机电耦合部分的微分方程，利用Matlab/Simulink数值仿真分析软件，采用ODE45求解器，即可仿真得到系统在时域内的动力学响应和压电元件输出电压。

在仿真过程中，激振加速度采用振幅为3 m/s2，频率为10～60 Hz的正向扫频信号；磁间距d的变化范围为20～40 mm；式(11)给出了压电能量收集器在无接口电路的情况下，产生最大输出功率所对应的最优负载计算公式[15]，因此计算得到阻值为114 kΩ和707 kΩ的匹配电阻分别接对应的压电元件1和2，仿真过程中匹配电阻的阻值不再变化。此时计算相应激振频率下通过电阻的电流值，即可计算得到压电悬臂梁各自的输出功率。两个压电悬臂梁的输出功率直接相加，最终可得到压电能量回收装置的总输出功率随激振频率变化的仿真关系曲线，如图3所示。

(11)

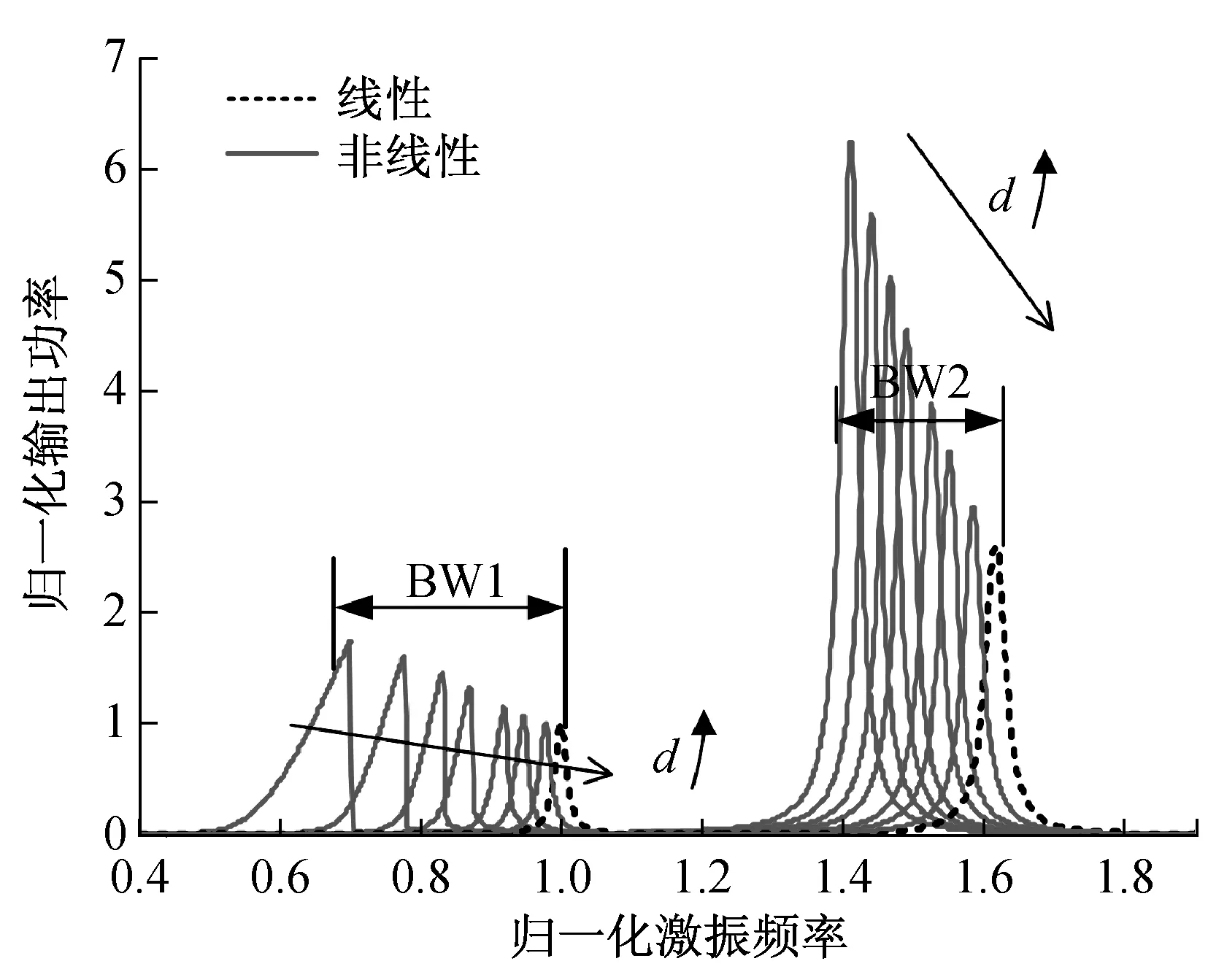
图3 不同磁间距下输出功率与激振频率的关系曲线图

Fig.3 The curves of the output powers as a function of excitation frequency under the different magnetic distances

图3中实线为压电能量回收结构在非线性条件下获得的总输出功率，即结构存在非线性磁力作用；虚线为两个线性压电悬臂梁各自的输出功率之和，悬臂梁之间不存在磁力作用。为方便比较，激振频率和输出功率均作了归一化处理：激振频率以线性压电悬臂梁1的一阶固有频率作归一化；输出功率以线性压电悬臂梁1的最大输出功率作归一化。

图3中的仿真结果可以看出改变磁间距d的大小能够明显调节悬臂梁1和2的共振频率：d越小，结构实际共振频率越低。利用该现象，实际能量回收结构就可以通过调节磁间距d的大小，让其中一个或两个悬臂梁去匹配环境振动源的激振频率，进而获得较高的输出功率。仿真结果可知该非线性能量回收结构共有两个较宽的工作频带：BW1和BW2，上限截止频率即为线性情况下对应悬臂梁的固有频率。值得指出的是在工作频带BW1和BW2内，能量回收结构的总输出功率均比对应线性情况下悬臂梁的输出功率高。

图4分别给出了两个压电悬臂梁在线性与非线性情况下各自的频响特性曲线，为简化仿真参数，悬臂梁的振幅以非线性条件下，磁间距d(d=24 mm)的值为参考量作了归一化处理。

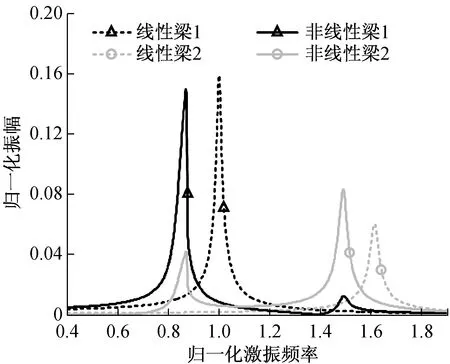
图4 压电悬臂梁振幅随激振频率变化关系曲线图(d=24 mm)

Fig.4 The vibration amplitude curves of the piezoelectric beams as a function of excitation frequency (d=24 mm)

通过图4可以发现当归一化激振频率为0.85时，虽然其远低于线性悬臂梁2的归一化固有频率1.61，但在非线性磁力的作用下，非线性悬臂梁2多出了一个振动模态，并在该模态下产生了较高的输出功率。参考图5中的振动位移放大图可以看出在此激振频率下，悬臂梁1和2的振动位移相位差约为180度。

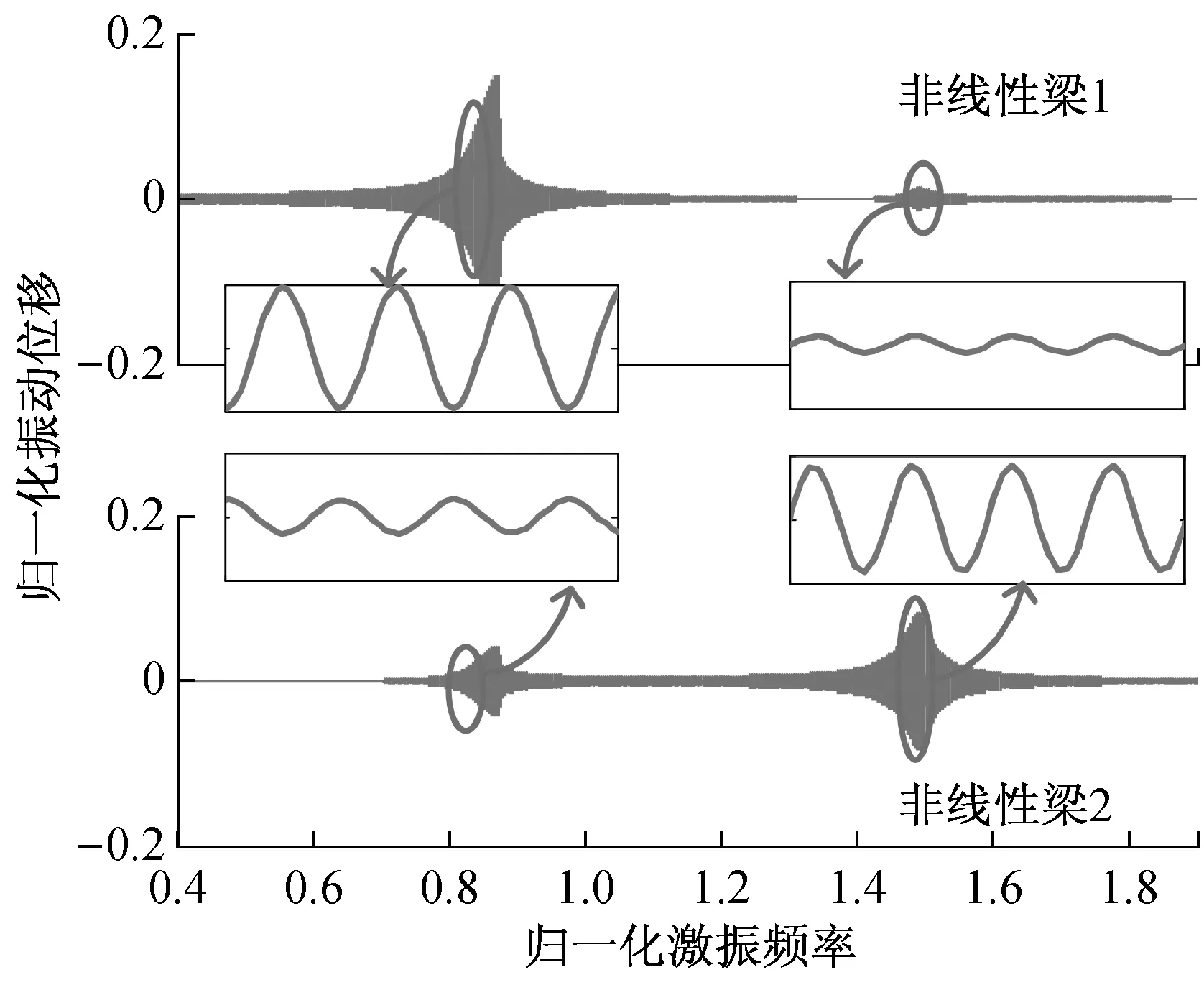
图5 非线性情况下压电悬臂梁振动位移随激振频率变化关系曲线图(d=24 mm)

Fig.5 The vibration displacement curves of the nonlinear piezoelectric beams as a function of excitation frequency (d=24 mm)

当归一化激振频率为1.5时，悬臂梁2的受迫振幅明显大于其在线性条件下的最大振幅，参考图5中的振动位移放大图可以看出在此激振频率下，悬臂梁1和2的振动方向几乎一致。对于振幅较大的悬臂梁2来说，作用在等效质量块2上的非线性磁力始终与其振动位移同方向，使其更容易获得较高地振幅，进而增加了压电悬臂梁2的机电转换效率。

3.2 实验结果及其讨论

图6所示为基于本文所述的闭环实验系统，压电振动能量回收结构在加速度幅值恒定的正弦激励下，通过改变磁间距d获得的输出功率频响曲线图。其中虚线为磁间距为40 mm时的测试结果，此时磁力FB可忽略，即认为悬臂梁1和2处于线性振荡状态；实线为结构处于非线性振荡状态下的实验结果，磁间距在20～32 mm之间变化。

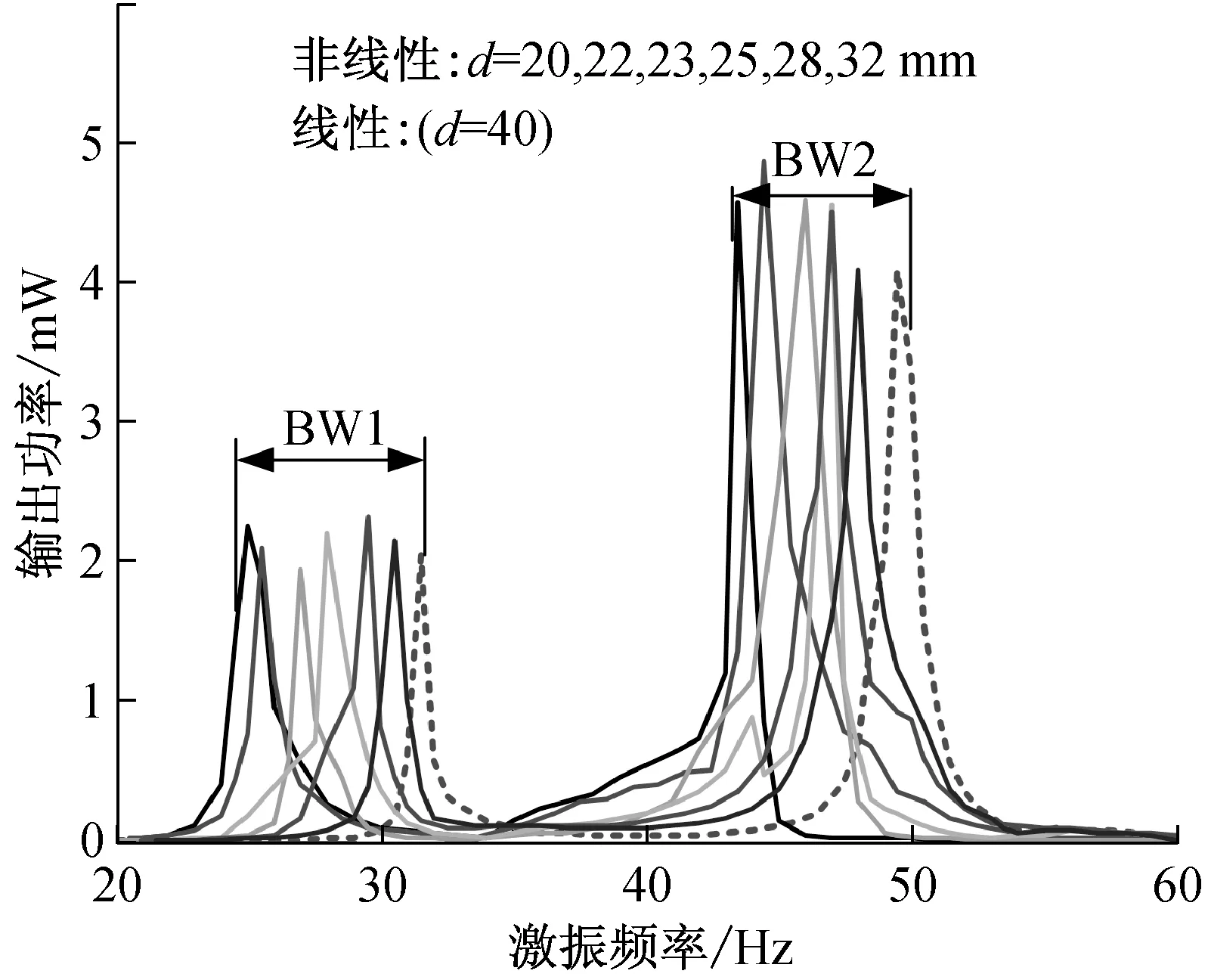
图6 不同磁间距下实际输出功率与激振频率的关系曲线图

Fig.6 The practical output power as a function of excitation frequency under the different magnetic distances

实验结果清楚地表明能量回收结构有两个较宽的工作频带BW1和BW2。其中BW1的带宽为7 Hz，略大于BW2的带宽6.5 Hz，与仿真结果一致。当外界激振频率在这两个工作频带范围内变化时，压电能量回收结构的总输出功率均大于2 mW。

需要指出的是，相比于仿真结果，实际结构在工作频带BW1和BW2内，总输出功率并没有显著提高。这主要是因为实际结构受到永磁体实际磁场以及加工、装配精度等因素的影响，磁力的等效作用点没有严格地落在悬臂梁的中性面内。因此对于悬臂梁2，在工作频带BW1内，磁力FB所做的功不恒等于0；在工作频带BW2内，磁力FB不能始终与压电悬臂梁2的中性面振动方向一致，导致悬臂梁2的振动不能被有效地激发或提高，大大降低了结构总的输出功率。

4 结 论

本文介绍了一种基于非线性磁力调节结构共振频率的压电振动能量回收结构。建立了理论模型并进行了仿真分析，实验结果表明：通过改变结构在初始状态下磁间距d的值，即可实现结构的共振频率匹配调节功能。由于结构同时具有两个较宽的工作频带，该能量回收装置特别适用于功率谱密度具有一个或两个峰值且会在小范围内随机缓慢改变的环境振动源。后续研究将设计该装置的共振频率自适应匹配系统，并着重优化控制系统的功耗和频率匹配速度，使所述结构具有更好的实际应用价值。

[1] BEEBY S P, TUDOR M J, WHITE N M.Energy harvesting vibration sources for microsystems applications[J].Measurement Science and Technology, 2006, 17: 175-195.

[2] 刘祥建，陈仁文.压电振动能量收集装置研究现状及发展趋势[J].振动与冲击，2012，31(6)：169-176.

LIU Xiangjian, CHEN Renwen.Current situation and developing trend of piezoelectric vibration energy harvesters[J].Jouranl of Vibration and Shock, 2012, 31(6): 169-176.

[3] STEVEN R A, HENRY A S.A review of power harvesting using piezoelectric materials (2003-2006)[J].Smart Materials and Structures, 2007, 16(3): 1-21.

[4] TANG L, YANG Y, SOH C K.Broadband vibration energy harvesting techniques, in Advances in energy harvesting methods[M].New York: Springer, 2013: 17-61.

[5] 曾平，刘艳涛，吴博达，等.一种新型压电式无线发射装置[J].吉林大学学报(工学版)，2006，36(增刊2): 78-82.

ZENG Ping, LIU Yantao, WU Boda, et al.A novel wireless electropult powered by piezoelectricity[J].Journal of Jilin University(Engineering and Technology Edition), 2006, 36(Sup2): 78-82.

[6] 胡洪平，高发荣，薛欢，等.低频螺旋状压电俘能器结构性能分析[J].固体力学学报，2007，28(1): 87-92.

HU Hongping, GAO Farong, XUE Huan, et al.Analysis on structure and performance of a low frequency piezoelectric power harvester using a spiral-shaped bimorph[J].Acta Mechanica Solida Sinica, 2007, 28(1): 87-92.

[7] 阚君武，徐海龙，王淑云，等.多振子串联压电俘能器性能分析与测试[J].振动与冲击，2013，32(22)：79-83.

KAN Junwu, XU Hailong, WANG Shuyun, et al.Performance analysis and test of an energy harvester with serial-connected piezodiscs[J].Jouranl of vibration and shock, 2013, 32(22): 79-83.

[8] EICHHORN C, GOLDSCHMIDTBOEING F, WOIAS P.A frequency tunable piezoelectric energy converter based on a cantilever beam[C].Proceedings of Power MEMS+micro EMS 2008, 2008: 309-312.

[9] PILLATSCH P, MILLER L M, HALVORSEN E, et al.Self-tuning behavior of a clamped-clamped beam with sliding proof mass for broadband energy harvesting[J].Journal of Physics: Conference Series.IOP Publishing, 2013, 476(1): 012068.

[10] ROUNDY S, ZHANG Y.Toward self-tuning adaptive vibration-based microgenerators[J].Smart Materials, Nano-, and Micro-Smart Systems.International Society for Optics and Photonics, 2005: 373-384.

[11] 马华安，刘景全，唐刚，等.一种宽频带磁式压电振动能量采集器[J].传感器与微系统，2011，30(4)：66-68.

MA Huaan, LIU Jingquan, TANG Gang, et al.A magnetic structure for broadband piezoelectric vibration energy harvester[J].Transducer and Mocrosystem Technologies, 2011, 30(4): 66-68.

[12] YUNG K W, LANDECKER P B, VILLANI D D.An analytic solution for the force between two magnetic dipoles[J].Physical Separation in Science & Engineering, 1998, 9(1): 39-52.

[13] LIN J T, LEE B, ALPHENAAR B.The magnetic coupling of a piezoelectric cantilever for enhanced energy harvesting efficiency[J].Smart Materials & Structures, 2010, 19(4): 126-134.

[14] WU Y, BADEL A, FORMOSA F, et al.Nonlinear vibration energy harvesting device integrating mechanical stoppers used as synchronous mechanical switches[J].Journal of Intelligent Material Systems and Structures, 2014, 25(14): 1658-1663.

[15] GUYOMAR D, BADEL A, LEFEUVRE E, et al.Toward energy harvesting using active materials and conversion improvement by nonlinear processing[J].IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2005, 52(4): 584-595.

A nonlinear piezoelectric vibration energy harvesting device with tunable resonance frequencies

WU Yipeng, JI Hongli, QIU Jinhao, ZHANG Hao

(State Key Laboratory of Mechanics and Control of Mechanical Structures, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China)

Vibration energy harvesting technology can convert ambient mechanical vibration energy into electrical energy and then powers micro-power consumption devices, it is an attractive technology for practical application.Here, a novel vibration energy harvesting device was designed based on piezoelectric materials, its electro-mechanical coupled structure was composed of a pair of asymmetric cantilevers, their free ends were glued with magnets.Fortunately, a nonlinear magnetic force caused by magnets was adopted to realize the matching adjustment between the resonance frequency of the cantilever and external excitation frequency.The theoretical model of the device’s structure was proposed.The model was simulated with MATLAB/Simulinke and verified with tests.The results showed that when the external excitation acceleration amplitude is 3 m/s2, the device can be used to realize the frequency matching adjustment within a wider frequency band range, the frequency band range is higher than 6.5 Hz and the maximum harvesting power is higher than 2 mW.

energy harvesting; frequency tuning; piezoelectric; nonlinear

国家自然科学基金(11532006)；江苏省青年基金(BK20130791)；江苏省博士后科研资助计划(1501025C)；中央高校基本科研业务费专项(NE2015001)；江苏高校优势学科建设工程；南京航空航天大学机械结构力学及控制国家重点实验室自主研究课题(0515Y02)

2016-01-07 修改稿收到日期：2016-02-20

吴义鹏 男，博士，讲师，1986年12月

季宏丽 女，博士，副教授，1983年2月

TB123；TB381

A

10.13465/j.cnki.jvs.2017.05.003