温压炸药爆炸冲击波在坑道内的传播规律研究

耿振刚，李秀地, 2，苗朝阳, 2，方 浩

(1.后勤工程学院 土木工程系，重庆 401311；2.后勤工程学院 岩土力学与地质环境保护重庆市重点实验室，重庆 401311)

温压炸药爆炸冲击波在坑道内的传播规律研究

耿振刚1，李秀地1, 2，苗朝阳1, 2，方 浩1

(1.后勤工程学院 土木工程系，重庆 401311；2.后勤工程学院 岩土力学与地质环境保护重庆市重点实验室，重庆 401311)

温压炸药爆炸冲击波对坑道内的人员和设备构成严重威胁。在TNT爆炸试验数据验证的基础上，利用AUTODYN软件建立了炸药堵口爆炸的数值计算模型。基于JWL-Miller能量释放模型计算原理，通过与TNT冲击波的对比，研究了某型温压炸药爆炸冲击波在坑道内的传播特性；通过与空旷地面爆炸冲击波的对比，研究了坑道对温压炸药爆炸冲击波的约束作用。研究结果表明：温压炸药具有更大的破坏威力，温压炸药的超压峰值和正相冲量平均为TNT的1.91倍和1.82倍，其超压和冲量等效TNT当量系数分别为1.94和2.21；坑道对温压炸药冲击波的约束作用明显，其超压峰值和正相冲量平均值分别为空旷地面上的13.55倍和15.21倍。

温压炸药；冲击波；坑道；JWL-Miller状态方程

温压弹是指利用温压炸药爆炸后的高温和高压效应产生杀伤效果的武器，它是在燃料空气弹的基础上发展而来的，与燃料空气弹原理相似，但是威力更强[1]。与普通高能炸药相比，温压炸药中添加了氧化剂以及一些活性金属粉末，这些粉末在高能炸药爆炸后起燃，并释放大量的热量。金属粉末的后燃反应使温压炸药的热效应和压力效应显著提高。

传统高爆炸药爆炸冲击波随传播距离衰减较快，对坑道深处的目标打击效果差；燃料空气炸药具有更强的爆炸威力，但其爆炸时需要从空气中吸取大量氧气，这限制了燃料空气炸药在打击坑道方面的应用；与燃料空气炸药比，温压炸药采用含有氧化剂的固体药剂，当固体药剂呈颗粒状在空气中散开，形成的爆炸杀伤力比燃料空气炸药更强；而且，温压炸药爆炸时无需大量空气，还能将有限空间内的氧气迅速耗尽，从而导致爆炸区内的人员因缺氧窒息而死。因此，温压弹更适合打击坑道等封闭空间内的人员和设备，开展温压炸药爆炸冲击波在坑道中的传播规律研究具有重要意义。

温压炸药坑道内爆炸冲击波传播的研究方法主要有试验研究和数值模拟分析。试验研究[2-4]是在构筑的模型坑道内进行温压炸药爆炸试验，根据实测数据来研究温压炸药爆炸冲击波在坑道内的传播规律。对温压炸药冲击波的数值模拟研究，主要有等效TNT法[5-6]、额外添加能量法[7-9]和用JWL-Miller能量释放模型法[10]。等效TNT法无法考虑温压炸药的后燃反应，在缺少温压炸药参数的情况下可近似应用；额外添加能量法是在温压炸药起爆后的某段时间内，通过向爆轰产物中额外加入铝粉燃烧热近似实现温压炸药的后燃反应[11]。但该方法无法合理确定所额外添加能量的大小和时间段。JWL-Miller能量释放模型法在由温压炸药爆炸试验准确确定模型参数的基础上，利用AUTODYN软件提供的JWL-Miller模型实现温压炸药的爆炸能量释放。该模型能够表示非理想炸药爆炸过程中的额外释放能量，材料参数由试验确定，所以该模型能够较准确地反映温压炸药的爆炸过程。

目前，应用JWL-Miller能量释放模型法研究坑道内温压炸药爆炸冲击波的传播规律，鲜见报道。本文首先利用AUTODYN软件建立了坑道内炸药爆炸的数值计算模型，并利用TNT爆炸试验数据验证了本文数值模型计算结果的可靠性。然后，基于JWL-Miller能量释放模型，通过与TNT冲击波对比，研究了某型温压炸药爆炸冲击波在坑道内的传播规律；通过与空旷地面冲击波的对比，研究了坑道对温压炸药爆炸冲击波的约束作用。研究成果可为坑道防护提供参考。

1 试验概况

笔者进行了TNT坑道堵口爆炸试验。在坑道侧墙不同位置布置压力传感器，传感器捕捉的冲击波压力信号经传输电缆传给信号适配器放大，再由数据采集及处理系统记录波形。试验原理如图1。

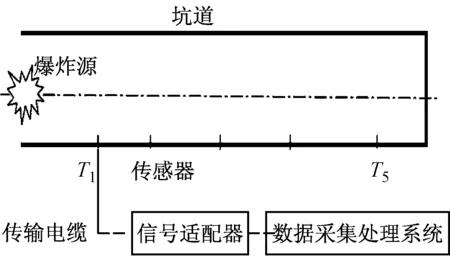
图1 冲击波测试原理Fig.1 Schematic diagram of blast test

试验采用钢筋混凝土直墙圆拱坑道，坑道截面积为0.67 m2。压力传感器与坑口距离分别为X=3.75 m、4.75 m、6.25 m、7.75 m、9.25 m。TNT药量为400～800 g。本文利用此次600 g TNT爆炸的冲击波实测数据验证本文所建立的坑口爆炸数值计算模型。600 g TNT在坑口截面中心爆炸的布置，见图2。

图2 坑道与装药布置Fig.2 Tunnel and charging arrangement

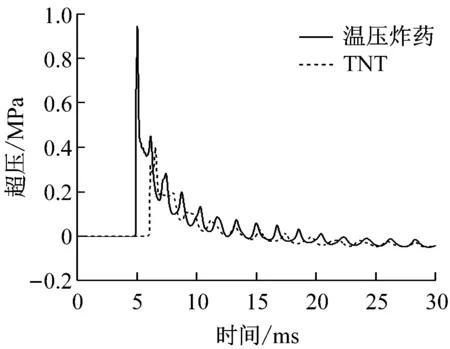
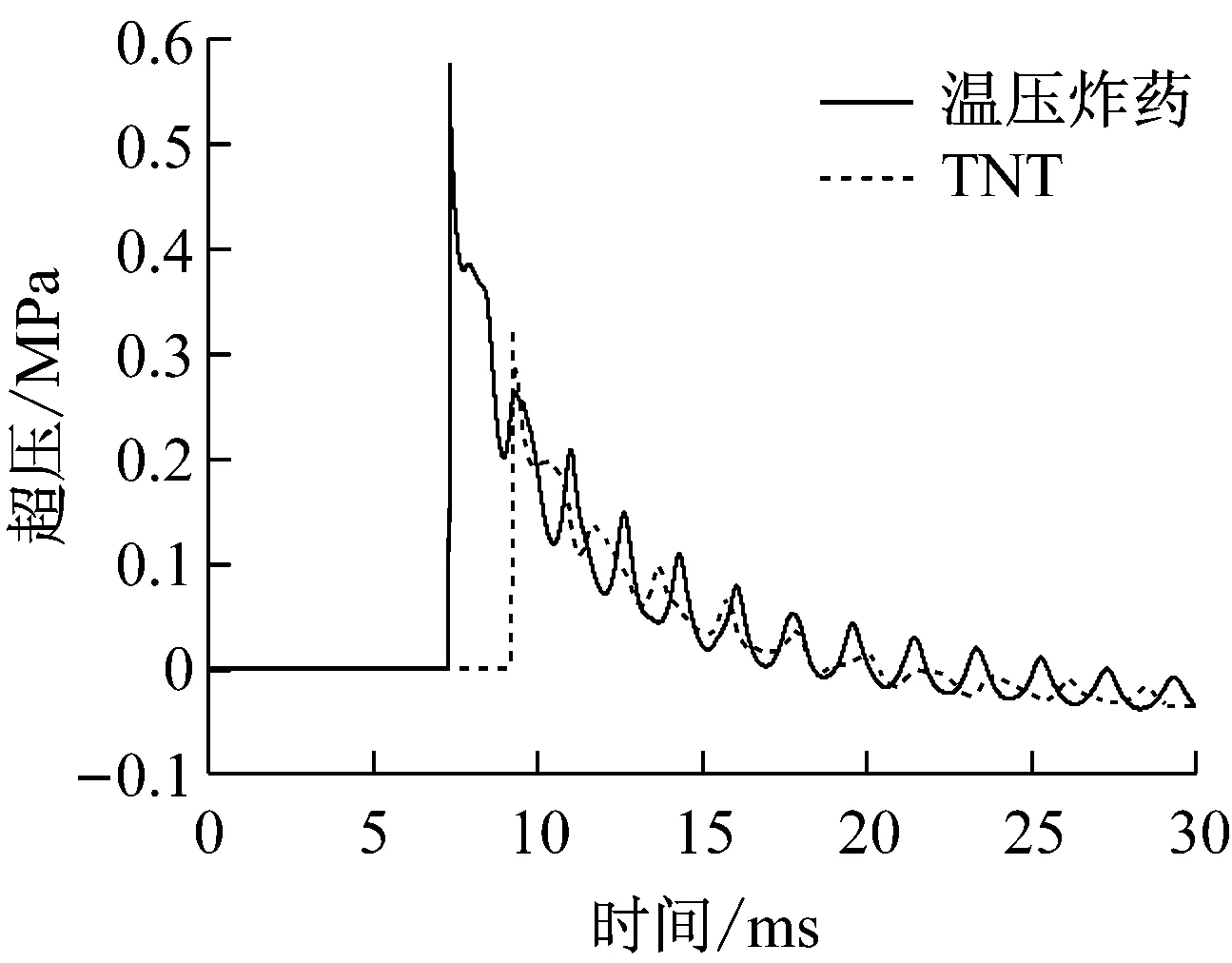
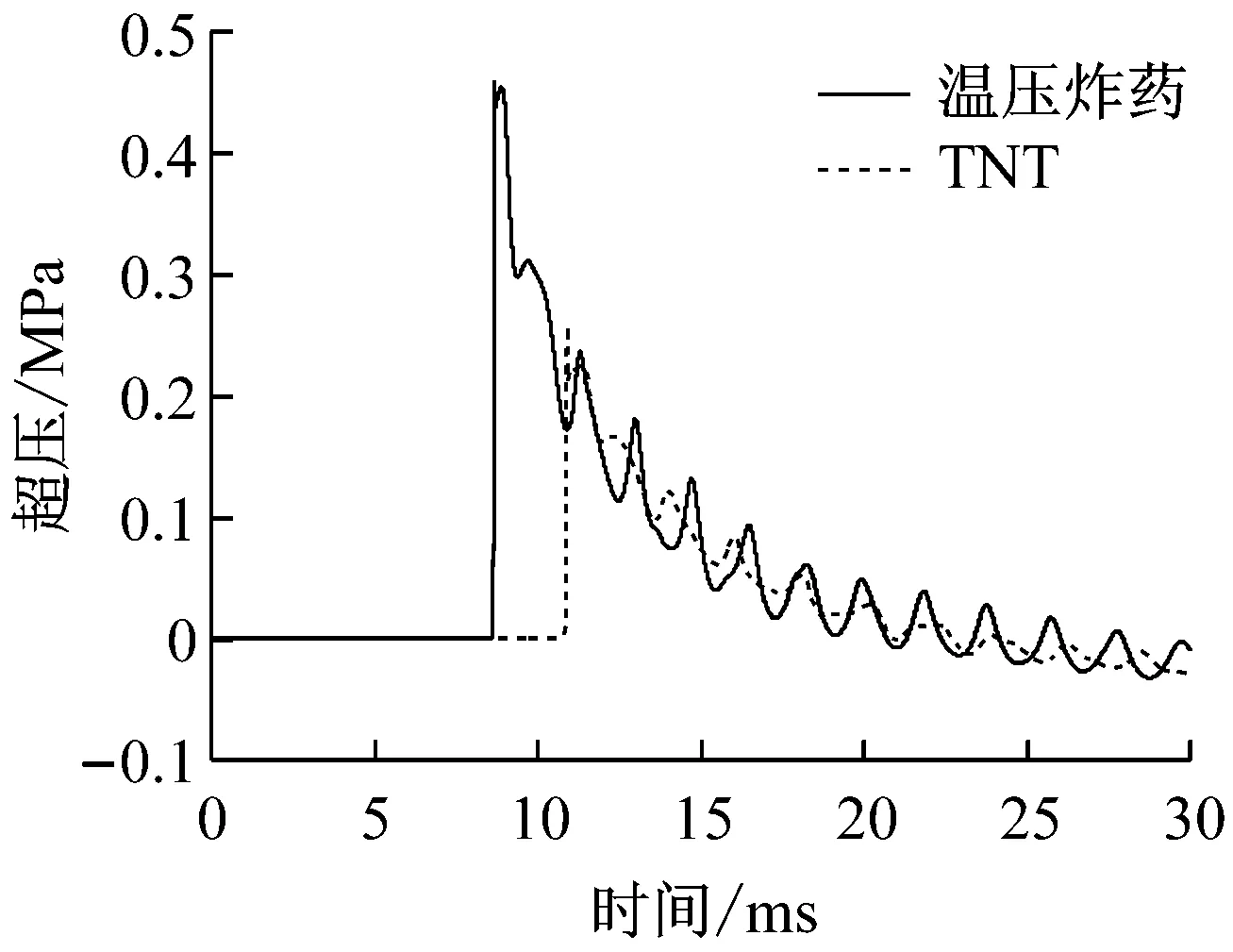
在距离3.75 m和6.25 m处的实测典型波形，见图3所示。

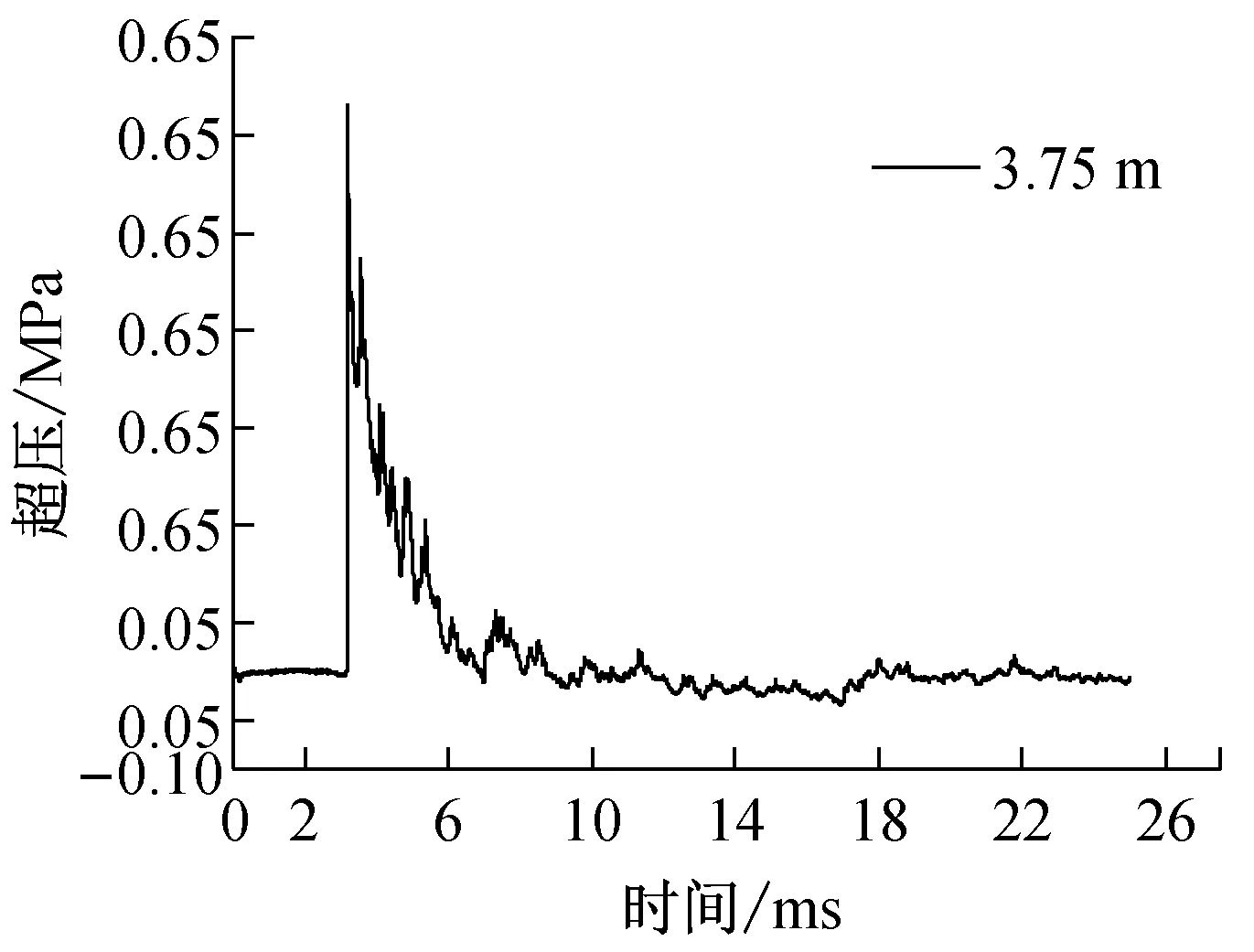
(a) X=3.75 m

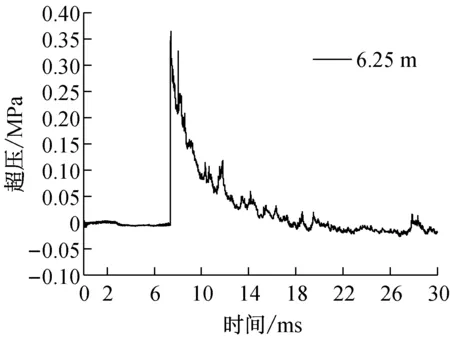
(b) X=6.25 m

2 数值模型的建立

2.1 计算模型

坑道截面等效为圆形，等效直径为0.92 m。本文采用AUTODYN软件建立轴对称的坑道堵口爆炸数值计算模型。坑道壁面刚性约束，计算域只由炸药和空气两部分组成，采用多物质欧拉求解器计算炸药的爆炸过程。炸药端坑道外建立长为100 mm的空气层，坑道两端均采用AUTODYN软件的“外流”(Flow-out)边界条件。炸药位于坑道口部截面中心，简化为等质量的球形装药。600 g TNT的等效半径为44.6 mm，同质量温压炸药的等效半径为42.6 mm。通过网格尺寸影响分析，网格尺寸取10 mm[12]。坑道长度为15 m，在坑道壁面每隔0.5 m设置一个监测点，记录冲击波波形。由于对称性，建立的二分之一模型，见图4。

图4 数值计算模型Fig.4 Calculation model for the tunnel

2.2 材料模型及参数

2.2.1 TNT

TNT材料采用经典的JWL状态方程描述，如式(1)所示

(1)

式中：P为压力；V为相对体积；E为内能密度；A、B、R1、R2、ω为材料常数。TNT材料的参数值[13]，如表1所示。

表1 TNT材料参数Tab.1 Parameters for TNT

2.2.2 温压炸药

温压炸药采用AUTODYN软件中的JWL-Miller能量释放模型[14]描述，如式(2)、(3)所示。

(2)

(3)

式(2)中：λ表示温压炸药中非理想组分的反应度；Q表示非理想组分在冲击面后额外释放的热量；其余符号含义同前。

式(3)表示温压炸药中非理想组分的反应速率方程。a为能量释放常数；m为能量释放指数；n为压力指数。

黄菊等对某型温压炸药能量输出结构进行了研究，并通过试验和数值模拟相结合的方法确定了温压炸药的JWL-Miller参数，如表2所示。

2.2.3 空气

空气的状态方程可近似采用理想气体状态方程描述。其状态方程表达式为

(4)

式中：Pa为空气压力；ρ为空气密度；ρ0为空气初始密度，取值为1.293×10-3g/cm3；γ为绝热指数，取值为1.4；E0为空气的初始比内能，取值为2.068×105μJ/mg。

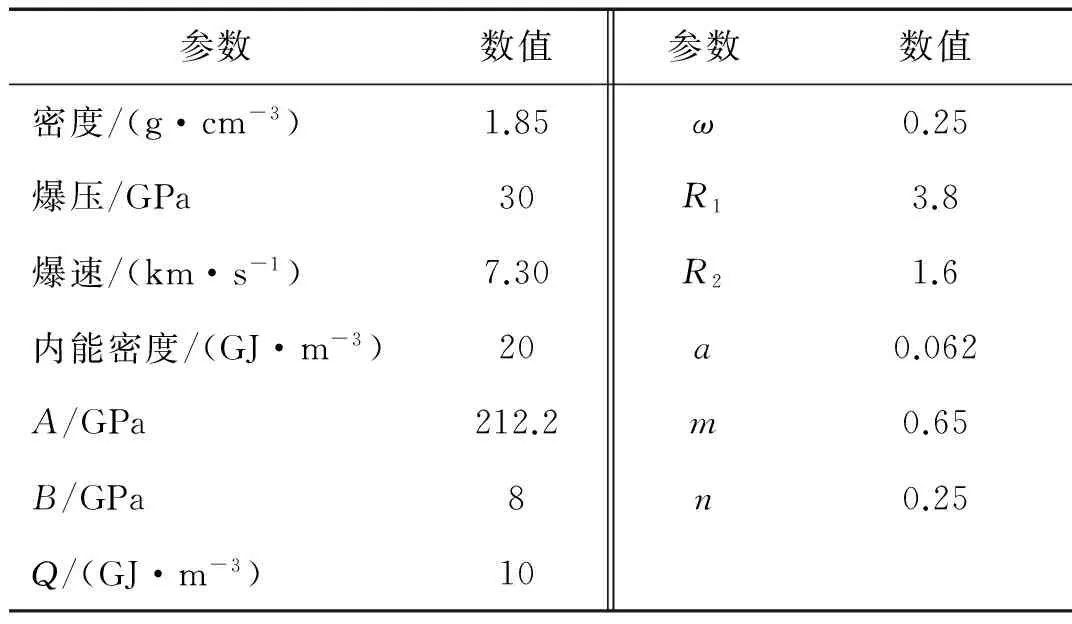
表2 温压炸药材料参数Tab.2 Parameters for thermobaric explosive

3 数值模型的试验验证

采用上述计算模型模拟600 g TNT堵口爆炸，各测点处的冲击波超压峰值、正相冲量值与实测值的比较如表3所示。

由表3可见，5个测点的峰值超压计算值与实测值误差最大为8.7%；对于正相冲量，第一个传感器距爆点较近，所测的实测波形比较杂乱，验证时不参加比较。其余四个测点的误差最大值为-12.6%，平均绝对误差(均按误差绝对值考虑)为7.2%。表明本文所建立的坑口爆炸数值计算模型能够较为准确地预测坑道内的冲击波参数，为本文下一步坑道内温压炸药爆炸冲击波的研究奠定了基础。

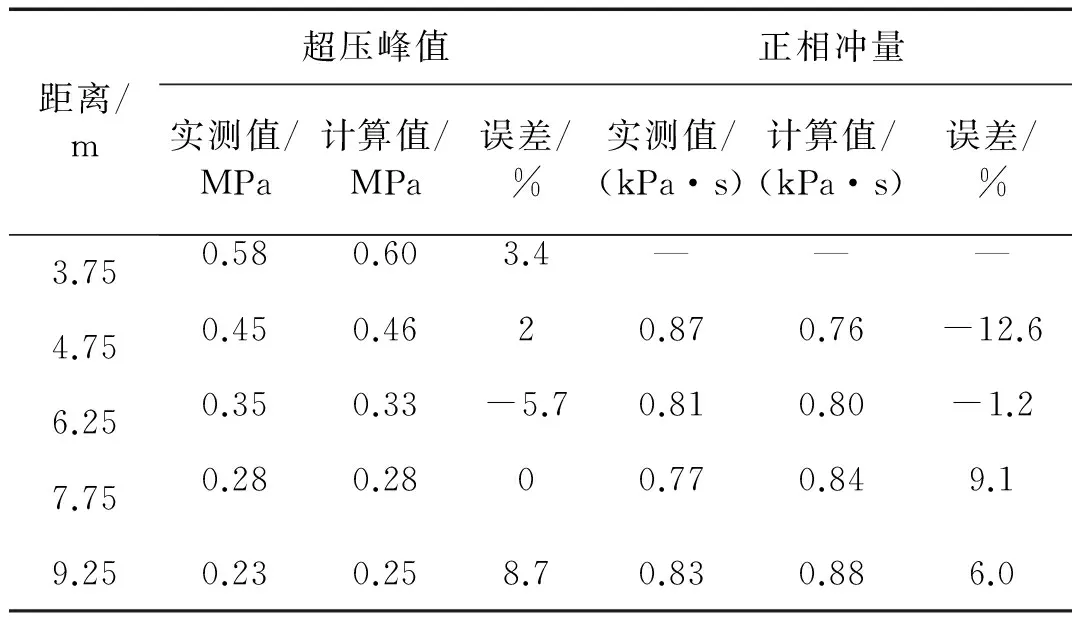
表3 冲击波参数计算值与实测值比较Tab.3 Comparison of calculation and test value of overpressure and impulse

4 坑道内温压炸药的传播规律研究

4.1 冲击波在坑道内的传播云图

温压炸药爆炸冲击波在坑道内不同时刻压力云图，如图5所示。从图中可以看出，温压炸药起爆后，由于受到坑道壁面的约束作用，冲击波在壁面间来回反射，反射波与入射波叠加不断向坑道内部传播。在爆炸初期大约t=1 ms前，冲击波比较杂乱；经过坑道壁面的多次反射，在大约t=6.65 ms后，逐渐形成了规则的平面冲击波。

(a) t=1 ms

(b) t=3.45 ms

(c) t=6.65 ms

(d) t=15.80 ms

4.2 冲击波波形分析

图6给出了距爆点X=6 m、8 m、9 m和10 m测点处温压炸药的冲击波波形。为便于对比，图中同时给出了相应的TNT冲击波波形。

(a) X=6 m

(b) X=8 m

(c) X=9 m

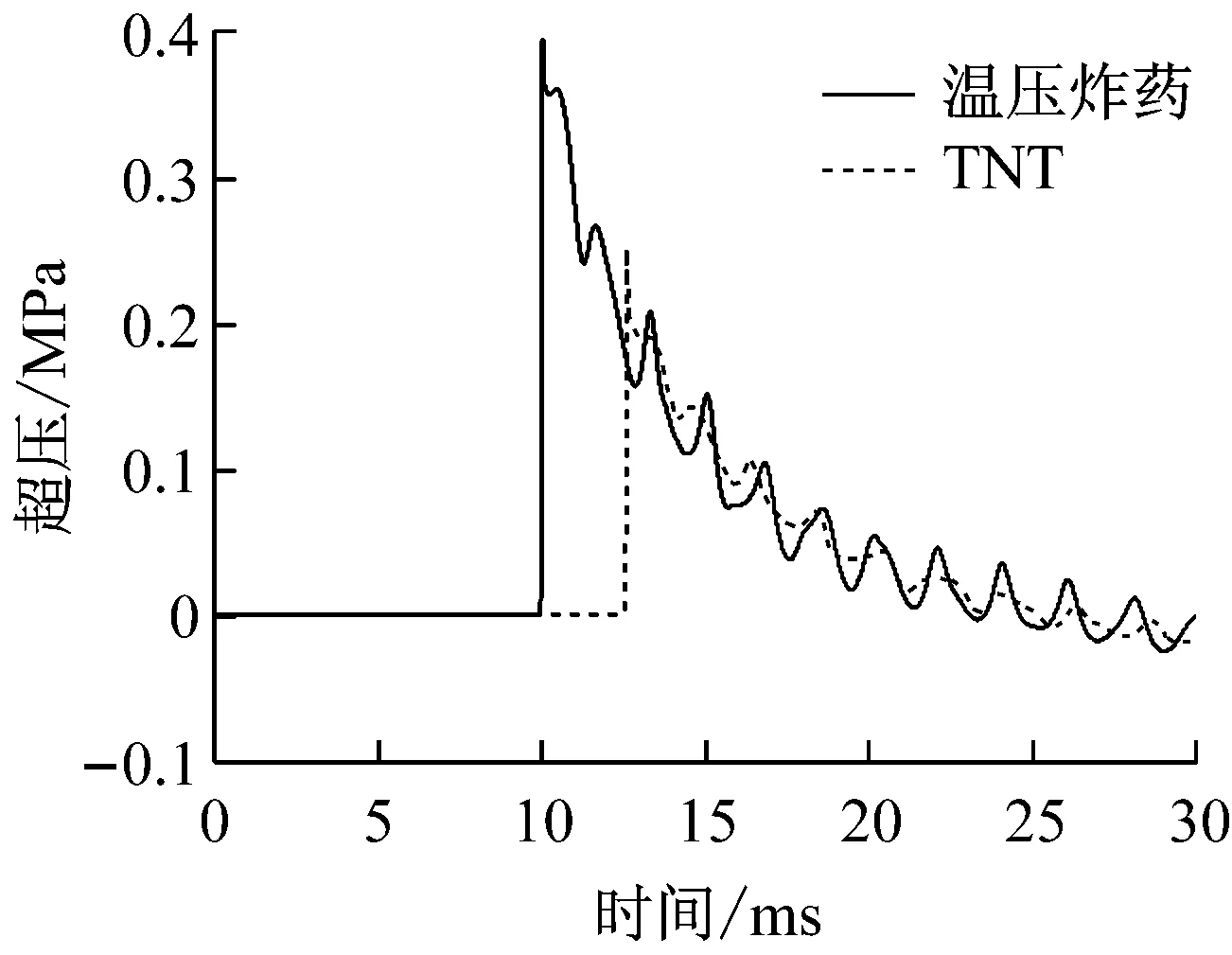
(d) X=10 m

从图6可以看出，在坑道壁面反射波的叠加作用下，坑道内的冲击波波形都呈明显的锯齿状，冲击波压力到达峰值后迅速衰减。与TNT比较可见，温压炸药爆炸冲击波首先到达，表明其传播速度更快；温压炸药的峰值压力、正相冲量、正相持续时间均大于TNT的相应值，表明温压炸药爆炸冲击波具有持续时间长、冲量高的特点，具有更大的破坏威力。

4.3 冲击波参数与传播距离的关系

两种炸药爆炸冲击波超压峰值和正相冲量沿坑道的变化规律，如图7所示。

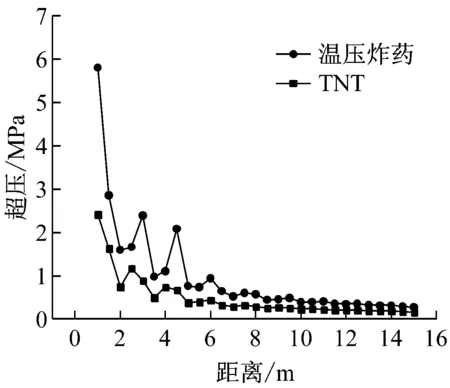
(a) 峰值压力

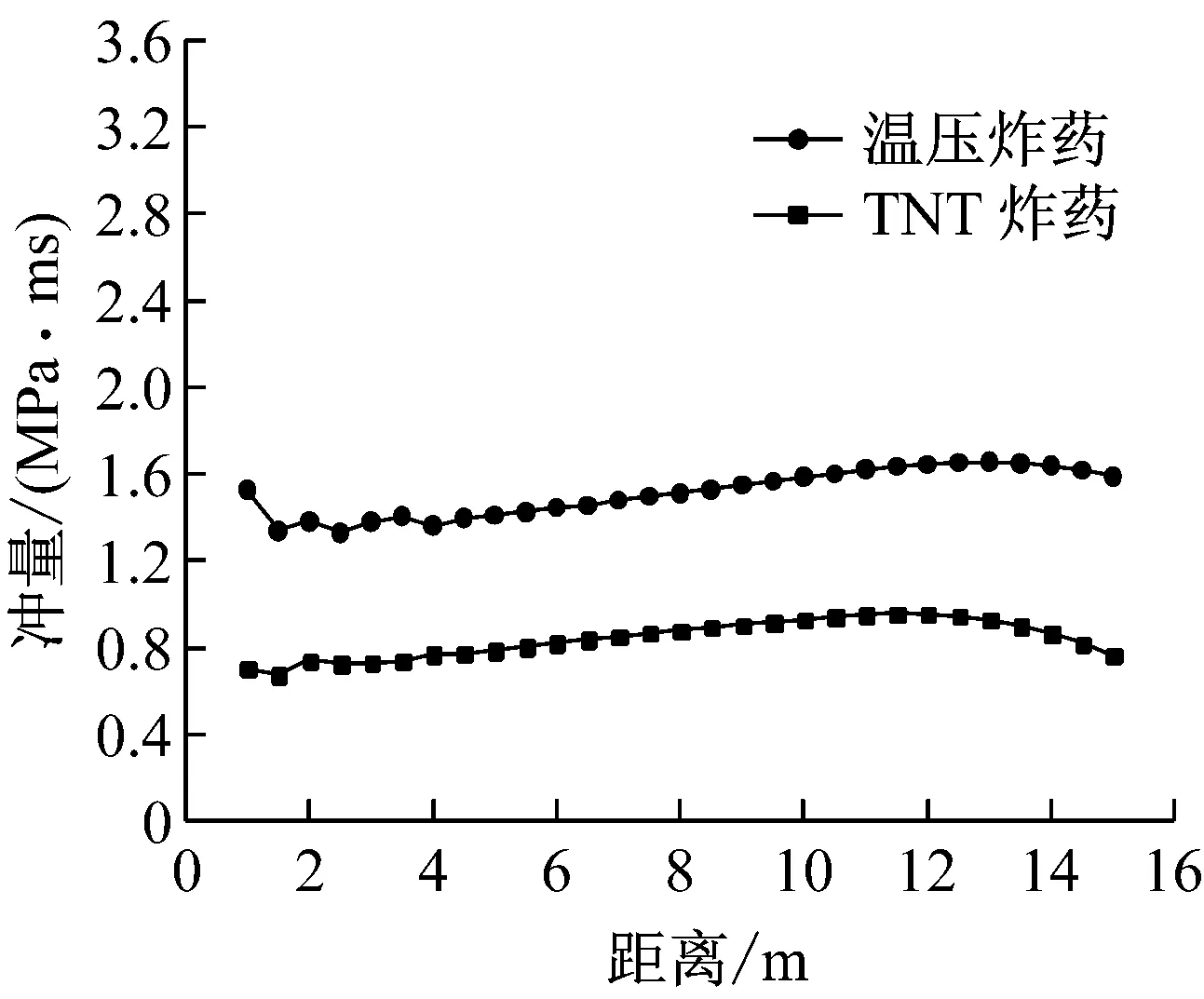
(b) 正相冲量

从图7(a)可以看出，在口部近区(约6 m前)，由于冲击波尚未形成平面波，随着传播距离的增加，冲击波压力衰减规律不稳定。平面波形成后(约6 m后)，冲击波压力随传播距离的增加而不断衰减。统计平面波形成后各测点的温压炸药超压峰值和对应距离处TNT超压峰值的比值，得到温压炸药的平均超压峰值约是TNT的1.91倍。

从能量守恒的角度出发，冲击波冲量随着传播距离的增大而不断减小。但从图7(b)可以看出，随着传播距离的增加，坑道内的冲击波正相冲量基本上首先不断增大，然后再不断衰减。这是因为在坑道口部附近的一段距离内，由于坑道壁面反射冲击波的叠加作用明显，不断增大了传播中的冲击波的正相冲量，这与前述坑道内冲击波具有锯齿状特征的结论一致。统计平面波形成后各测点的温压炸药正相冲量和对应距离处TNT正相冲量的比值，得到温压炸药的平均正相冲量约是TNT的1.82倍。

4.4 温压炸药的TNT当量计算

TNT堵口爆炸坑道内冲击波超压和冲量随距离衰减的经验计算公式[15-16]可表示为

(5)

I=1.2D(W/D3)0.6

(6)

式中：ΔPi为超压峰值(MPa)；W为TNT药量(kg)；S为坑道截面积(m2)；X为计算点到爆心的距离(m)。I为冲击波正相冲量(kPa·s)，D为坑道等效直径(m)。

利用上述TNT堵口爆炸情况下坑道内冲击波超压和冲量的已有经验计算公式，将本文数值模拟得到的温压炸药爆炸冲击波峰值压力和正相冲量值代入反推，即可得到相应的等效TNT药量，从而得到温压炸药的等效TNT当量系数，如表4和表5所示。

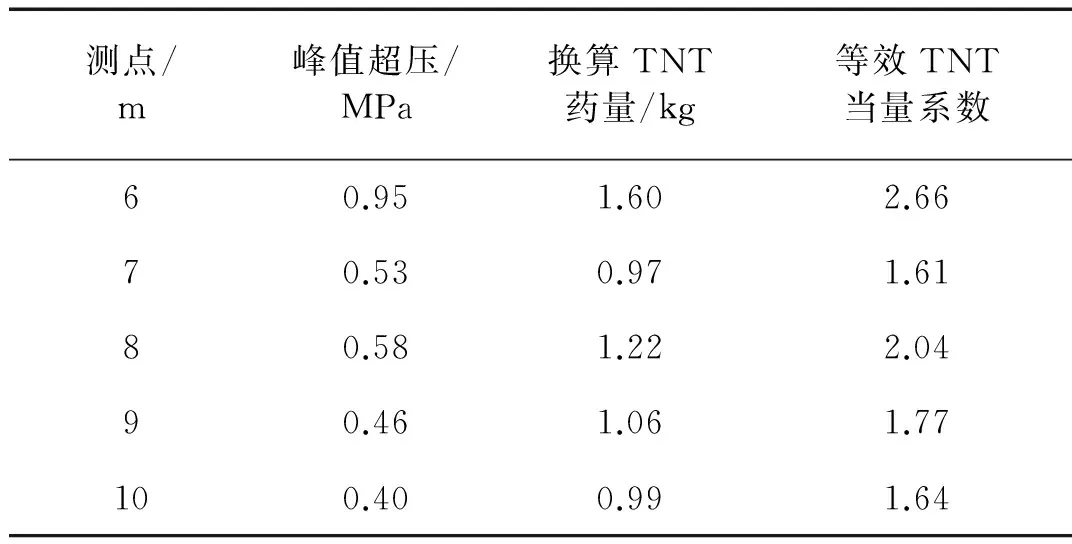
表4 温压炸药各截面超压等效TNT当量计算Tab.4 The TNT equivalence of TBE at different measuring position of overpressure

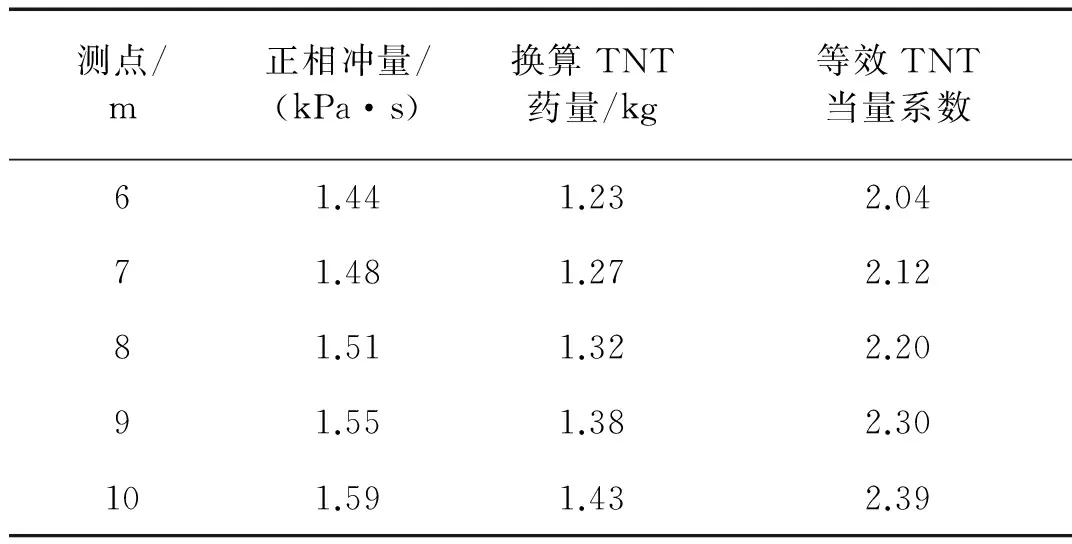
表5 温压炸药各截面冲量等效TNT当量计算Tab.5 The TNT equivalence of TBE at different measuring position of impulse

由表4可知，坑道内不同距离处温压炸药的超压等效TNT当量系数并不相等。除了测点7 m处因压力波动偏小外，随着传播距离的增大，温压炸药的超压等效TNT当量系数逐渐减小。本文取不同距离处等效TNT当量系数的平均值，作为温压炸药的平均压力等效TNT当量系数。计算表明，不同距离处的压力等效TNT当量系数介于1.61～2.66之间，温压炸药的平均压力等效TNT当量系数为1.94。

由表5可知，随着传播距离的增加，温压炸药的冲量等效TNT系数逐渐增加。因此，相对TNT来言，温压炸药爆炸冲击波的持续时间更长、冲量更高，特别适合于打击坑道等地下工程。计算表明，不同距离处的冲量等效TNT当量系数介于2.04～2.39之间，该温压炸药的平均冲量等效TNT当量系数为2.21。

5 坑道对温压炸药冲击波的约束作用

为分析坑道对温压炸药冲击波的约束作用，建立温压炸药在空旷地面爆炸的二维轴对称计算模型，温压炸药药量仍为600 g，如图8所示。其中，地面设置为刚性约束。

表6给出了温压炸药在坑道内和空旷地面距爆点相同距离处的峰值超压值和正相冲量值。

由表6可以看出，在距爆点3～7 m的各个测点处，温压炸药爆炸冲击波在坑道内的超压为在空旷地面上的11.74倍～15.31倍，平均为13.55倍。温压炸药爆炸冲击波在坑道内的冲量为在空旷地面上的12.24倍～16.69倍，平均为15.21倍。这一模拟结果与LUNDERMAN等[17]关于坑道对爆炸冲击波约束作用的研究成果基本一致。表明由于坑道壁的约束作用，温压炸药爆炸冲击波的压力和冲量会大大增强。

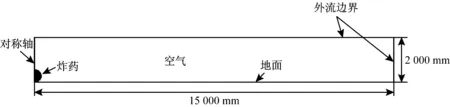
图8 空旷地面计算模型Fig.8 Schematic diagram of the calculation model on the open ground

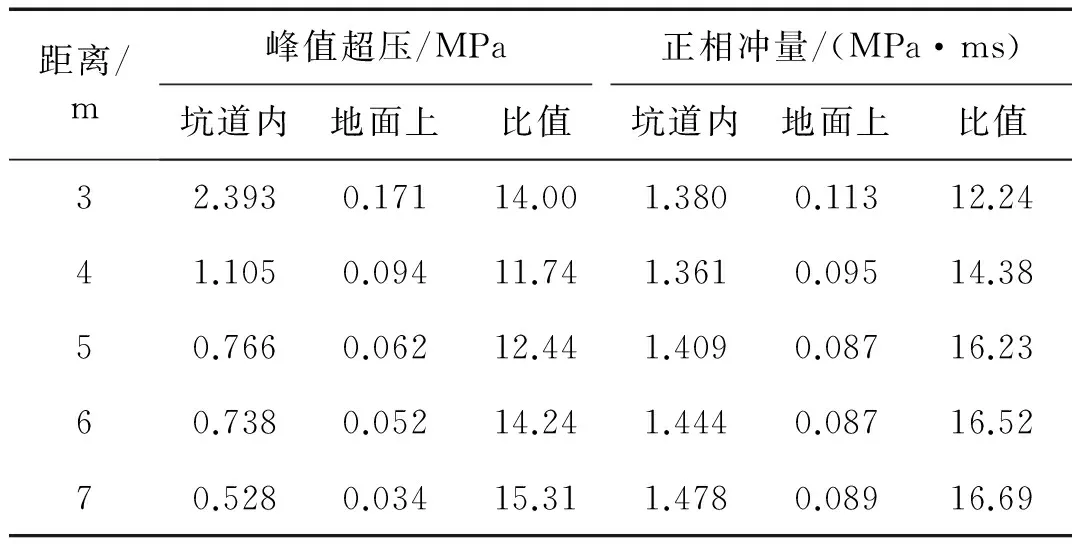
表6 坑道内和空旷地面的超压和冲量比较Tab.6 Comparison of overpressure and impulse of TBE in the tunnel and on unconstrained ground

6 结 论

本文基于JWL-Miller能量释放模型，研究了某型温压炸药爆炸冲击波在坑道内的传播规律，可以得到以下结论：

(1)与TNT爆炸实测数据比较表明，本文数值计算得到的坑道内冲击波峰值超压最大误差为8.7%，正相冲量平均绝对误差为7.2%。表明本文建立的数值计算模型能够较为准确地预测坑道内的爆炸冲击波。

(2)本文计算条件下，坑道内部温压炸药爆炸冲击波的所有测点处的平均峰值超压是TNT的1.91倍，温压炸药的平均正相冲量为TNT的1.82倍。该温压炸药的平均超压等效TNT当量系数为1.94，平均冲量等效TNT当量系数为2.21。表明温压炸药具有更大的破坏威力。

(3)温压炸药爆炸冲击波在坑道内的超压为在空旷地面上的11.74倍～15.31倍，平均为13.55倍。温压炸药爆炸冲击波在坑道内的冲量为在空旷地面上的12.24倍～16.69倍，平均为15.21倍。表明坑道壁面的约束作用会大大增强温压炸药的爆炸冲击波效应。

[1] 郭美芳,阎向前.从燃料空气弹到温压弹[J].现代军事,2002(3):21-23.

GUO Meifang,YAN Xiangqian.From the fuel and air bomb to the thermboric bomb[J].Modern Military, 2002(3):21-23.

[2] 孔霖,苏健军,李芝绒,等.不同装药坑道内爆炸冲击波传播规律的试验研究[J].火工品，2012(3):21-24.

KONG Lin,SU Jianjun,LI Zhirong, et al.Experimental study of explosive wave propagation of different charge in tunnel[J].Initiators & Pyrotechnics, 2012(3):21-24.

[3] 苟兵旺,李芝荣,闫潇敏,等.复杂坑道内温压炸药冲击波实验研究[J].火工品,2014(2):41-45.

GOU Bingwang,LI Zhirong,YAN Xiaomin, et al.Experimental study of thermobaric explosive wave in complex tunnel[J].Initiators & Pyrotechnics, 2014(2):41-45.

[4] 徐利娜,雍顺宁,王凤丹.直坑道内爆炸冲击波超压传播规律研究[J].测试技术学报，2014,28(2):114-118.

XU Lina, YONG Shunning, WANG Fengdan.Explosion overpressure propagation Study in straight tunnel[J].Journal of Test and Measurement Techol, 2014,28(2):114-118.

[5] 苗朝阳,李秀地,孙伟,等.温压弹爆炸冲击波作用下防护门的动力响应[J].四川兵工学报,2015,36(10):51-54.

MIAO Chaoyang, LI Xiudi, SUN Wei, et al.Dynamic response of protective door under the blast wave[J].Journal of Sichuan Ordnance, 2015,36(10):51-54.

[6] 赵新颖,王伯良,惠君明,等.温压炸药爆炸场参数的试验研究与数值模拟[J].火工品,2011(1):31-34.

ZHAO Xinying, WANG Boliang, HUI Junming, et al.Experimental study and numerical simulation of thermboric explosive parameters[J].Initiators & Pyrotechnics, 2011(1):31-34.

[7] 李世民,李晓军,李洪鑫.温压炸药坑道内爆炸冲击波的数值模拟研究[J].应用力学学报,2012,29(5):595-600.

LI Shimin, LI Xiaojun, LI Hongxin.Numerical simulation research of thermobaric blast wave in the tunnel[J].Chinese Journal of Applied Mechanics, 2012,29(5):595-600.

[8] 李世民,李晓军,郭彦朋.温压炸药自由场爆炸空气冲击波的数值模拟研究[J].爆破,2011,28(3):8-12.

LI Shimin, LI Xiaojun, GUO Yanpeng.Numerical simulation of thermobaric blast wave in the free atmosphere[J].Blasting, 2011,28(3):8-12.

[9] 茅靳丰,陈飞,侯普民.温压炸药坑道口部爆炸冲击波毁伤效应研究[J].力学季刊,2016,37(1):184-193.

MAO Jinfeng, CHEN Fei, HOU Pumin.Research on damage effect of thermobaric shockwave at the entrance of the tunnel[J].Chinese Quarterly of Mechanics, 2016,37(1):184-193.

[10] 黄菊,王伯良,仲倩,等.温压炸药能量输出结构的初步研究[J].爆炸与冲击,2012,32(2):164-168.

HUANG Ju, WANG Boliang, ZHONG Qian, et al.Preliminary study on energy output structure of thermobaric explosive[J].Explosion and Shock Waves, 2012,32(2):164-168.

[11] AUTODYN explicit software for nonlinear dynamics user manual[M].Pennsylvania, US: ANSYS Inc,2005.

[12] 杨坤,陈朗,伍俊英,等.计算网格与人工粘性系数对炸药水中爆炸数值模拟计算的影响分析[J].兵工学报,2014,35(增刊2):237-243.

YANG Kun,CHEN Lang,WU Junying, et al.Impact analysis of computational grid and artificial viscosity coefficient to simulation of underwater explosion[J].Acta Armamentarii, 2014,35(Sup2):237-243.

[13] AUTODYN theory manual[M].California Century Dynamics,2006.

[14] MILLER P J.A reactive flow model with coupled reaction kinetics for detonation and combustion of non-ideal explosives[C]//Proceedings of the Symposium on Decomposition,Combustion,and Detonation Chemistry of Energetic Materials.Boston, Massachusetts,1995:413-420.

[15] 杨科之,杨秀敏.坑道内化爆冲击波的传播规律[J].爆炸与冲击,2003,23(1):37-40.

YANG Kezhi, YANG Xiumin.Shock waves propagation inside tunnels[J].Explosion and Shock Waves, 2003, 23(1): 37-40.

[16] 陈海天, 李秀地, 郑颖人.内爆炸坑道中冲击波冲量试验[J].后勤工程学院学报, 2008, 24(2):6-8.

CHEN Haitian, LI Xiudi, ZHENG Yingren.Scale model tests to determine In-tunnel blast impulse from HE-charges inside the tunnel entrance[J].Journal of Logistical Engineering University, 2008, 24(2): 6-8.

[17] LUNDERMAN C, OHRT A P.Small-scale experiments of in-tunnel airblast from external and internal detonations[C]//Proceeding of the 8th International Symposium on Interaction of the Effects of Munitions with Structures.Mclean Virginia, USA, 1997:209-221.

Propagation of blast wave of thermobaric explosive inside a tunnel

GENG Zhengang1, LI Xiudi1, 2, MIAO Chaoyang1, 2, FANG Hao1

(1.Department of Architectural and Civil Engineering, Logistical Engineering University, Chongqing 401311, China；2.Chongqing Municipal Key Laboratory of Geomechanics & Geoenvironment Protection, Logistical Engineering University, Chongqing 401311, China)

Blast wave of thermobaric explosive is a serious threat to personnel and equipment inside a tunnel.Firstly, based on TNT blast test data verification, a numerical calculation model for an explosion entrance was established with the software AUTODYN.Secondly, the blast wave propagation characteristics inside a tunnel of thermobaric explosive whose state equation was described with JWL-Miller energy release model were studied through comparing with those of TNT blast wave.The constraint effect of a tunnel on the blast wave of thermobaric explosive was also investigated through comparing the propagation characteristics of thermobaric explosive side a tunnel with those on unconstrained ground.The results showed that thermobaric explosive has a greater destructive power; the average peak overpressure and positive phase impulse of thermobaric blast wave are1.91 times and 1.82 times of those of TNT, respectively; the equivalent coefficients of average overpressure and impulse of TNT for thermobaric explosive are1.94 and 2.21, respectively; the tunnel constrain effect on the blast wave of thermobaric explosive is obvious, the average peak overpressure and positive impulse of thermobaric shock wave in a tunnel are 13.55 times and 15.21 times of those on unconstrained ground.

thermobaric explosive; blast wave; tunnel; JWL-Miller state equation

全军后勤科研计划项目(CY213J009)；后勤工程学院学术创新基金(YZ0742202)

2016-05-30 修改稿收到日期：2016-07-13

耿振刚 男，硕士生，1990年生

李秀地 男，博士，教授，博士生导师，1970年生 E-mail:lixixudivip@163.com

O389

A

10.13465/j.cnki.jvs.2017.05.005