风电装备行星轮系过盈接触特性分析

向 东，沈 岗，朱 戡，沈银华，蒋 李

(清华大学 机械工程系，北京 100084)

风电装备行星轮系过盈接触特性分析

向 东，沈 岗，朱 戡，沈银华，蒋 李

(清华大学 机械工程系，北京 100084)

风力发电对于保障我国能源安全具有重大意义，但我国风电装备发展中还存在巨大技术瓶颈，如何进一步提高装备可靠性及寿命是亟需解决问题。以行星轮系过盈配合面接触特性与微动磨损关系为切入点，针对NGW型行星轮受力分析，计算获取过盈配合接触分析的载荷边界条件；通过对比不同过盈量在无外载工况下的配合面压力值，理论计算与仿真分析结果的平均误差约为5.74%，验证了仿真的可信度；通过对比不同过盈量在无外载下的变形量，行星轮内孔面与轴承外圈变形占比分别为89.5%和10.5%，定量描述了行星轮相较于轴承的变形程度，更易损伤；稳态载荷工况下，通过对比不同配合公差P6和R6下的最大微动滑移量可知，P6公差带下最大微动量随载荷变化幅度较大，因此风电行星轮配合公差应选R6更合适；非稳态载荷工况下，通过数值积分计算获取不同过盈量下的配合面打滑极限载荷，该极限值作为评定实际服役工况下出现剧烈“打滑现象”的准则，因此设计时应考虑该极限工况。

风电装备；过盈配合；配合公差：微动滑移；打滑现象

风力发电是国家能源安全的重要保障，近几年，风能开发在我国得到高速发展，目前风力发电已成为第三大主力电源。但我国风电装备发展中还存在巨大技术瓶颈，不稳定的阵风、频繁启停及低电压穿越等产生的瞬时载荷甚至超过设计载荷的3倍，恶化动力传动系统零部件关键接触面的性能，诱发失效，导致停机时间已占设计机时的23.9%，带来了巨大损失。

在风电齿轮箱行星轮系中，行星轮与轴承外圈往往采用过盈配合的形式。由于载荷波动，配合面会产生微动滑移现象，当外载波动程度较大时，甚至会出现打滑现象。该微动滑移或打滑现象往往会造成结合界面的微动磨损，影响装备的整体可靠性。针对过盈配合中微动滑移现象及其对结构性能的影响机制，不少学者开展了详细研究[1]。JUUMA[2]研究配合面接触应力和微动幅值对扭转微动疲劳极限的影响，发现随着接触压力增大，配合面间的滑移幅值降低，微动磨损也随之降低；GUTKIN等[3-4]研究过盈配合体在弯扭载荷下微动疲劳裂纹的扩展并与已有的实验数据对比分析，实验发现相对于纯弯矩作用，弯扭共同作用下的疲劳裂纹扩展寿命下降较大，约为50%；LEE等[5]研究循环弯矩作用下过盈配合接触面的微动磨损特征及表面形貌的演变，发现在疲劳循环初期时，接触边界磨损量最大，随着循环的增加，磨损区域逐渐向内部移动；LANOUE等[6-8]研究了滑动幅值与微动疲劳极限之间关系，并对比分析几种不同的疲劳准则，发现DANG VAN准则较符合实际；ALFREDSSON[9]通过实验和仿真结合方法研究过盈配合表面的微动演变，发现在单向滑移区和圆周滑移区出现了不同程度、不同形貌的磨损。

以上研究大多聚焦于过盈配合体受到扭矩作用时配合面的微动滑移及磨损问题上，由于风电装备行星轮与外圈、太阳轮啮合位置处受力方向相同，并未形成扭矩，因此行星轮与轴承配合面的微动特征与扭矩作用下的微动特征有一定区别，造成的磨损机理也有所差异，仍需进一步探究，本文正是基于这一点开展相关研究工作。

1 风电装备行星轮力学参数确定

开展行星轮内孔与轴承外圈过盈接触特性分析研究首先需要确定风电装备行星轮所受载荷参数。某型1.5 MW齿轮箱几何参数如表1所示，由于风机实际运行中二级行星轮系的失效破坏较为严重，因此本文主要针对二级行星轮建立有限元模型开展过盈特性分析。风电二级行星轮系为NGW型行星传动，受力分析如图1所示。图中，X是行星架；C是行星轮；A是太阳轮；B是外齿圈；TX是输入扭矩；TA是反作用扭矩。对于行星轮C而言，FtBC是齿圈施加的圆周力；FtAC是太阳轮施加的圆周力；FrBC是齿圈施加的径向力；FrAC是太阳轮施加的径向力；Rx′C是销轴施加的支反力。各构件在输入扭矩作用下都处于平衡状态，构件间的作用力等于反作用力。已知二级行星轮行星架输入端扭矩为TX=1.65×105N·m，太阳轮输出端扭矩为TA=2.91×104N·m，根据力平衡条件计算的行星轮载荷参数为

(1)

图1 二级行星轮受力分析Fig.1 Force Analysis of secondary planet gears

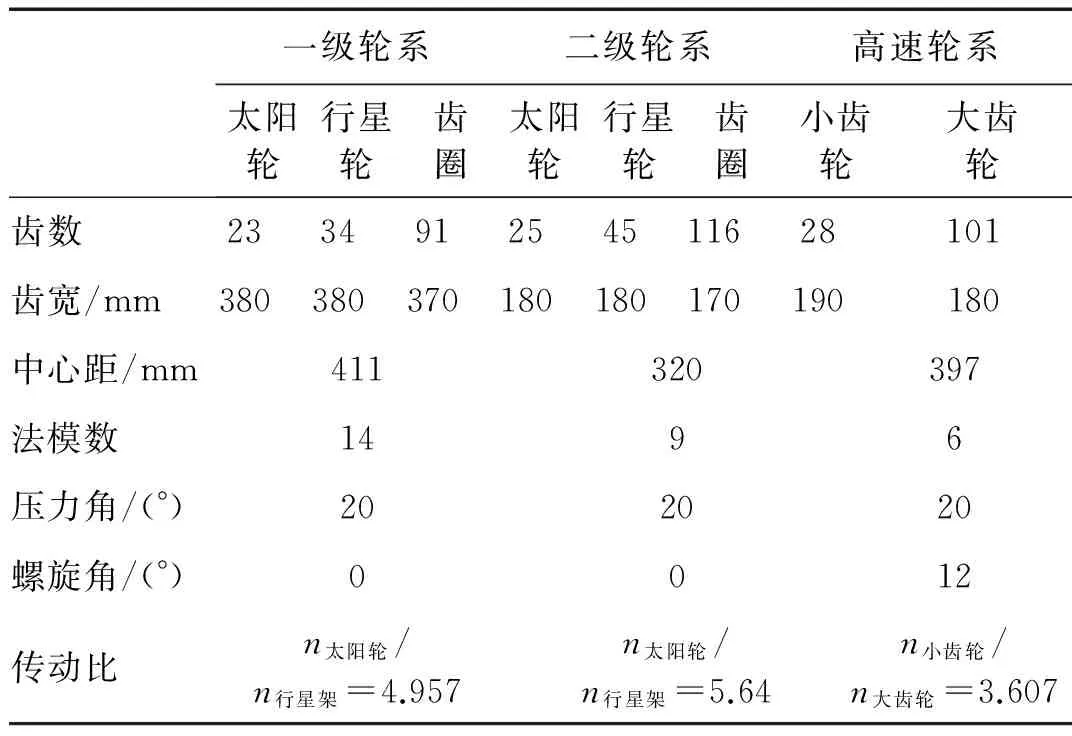
表1 某型1.5 MW齿轮箱几何参数Tab.1 Geometric parameters of 1.5 MW gearbox

2 无外载下过盈配合接触特性分析

本文所涉及的1.5 MW齿轮箱行星轮内孔与轴承外圈采用的配合公差为P6(过盈量为0.012 mm～0.079 mm)，此外其他某风电齿轮箱制造商采用的配合公差为R6(过盈量为0.054 mm～0.121 mm)。因此通过对比分析不同配合公差下的接触特性，可有效减少微动磨损效应，进而指导齿轮箱行星轮的设计。

在获取行星轮载荷参数与配合参数基础上，再结合关键部件行星轮与轴承的材料特性，如图2所示，可形成行星轮系有限元分析的边界条件。后续基于Ansys软件可以开展行星轮内孔与轴承外圈过盈接触状态下的压力与变形分析。

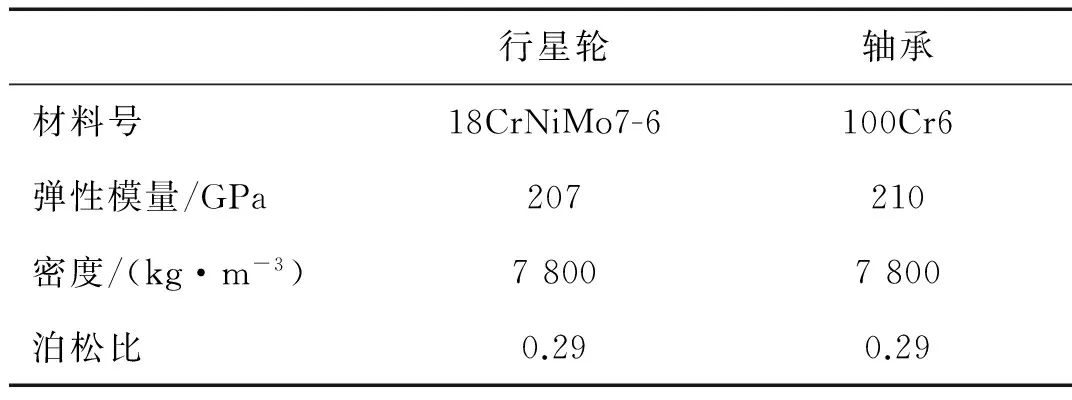
表2 部件材料参数Tab.2 Material parameters of parts

2.1 无外载下配合面压力值

在理论计算方面，根据材料力学有关厚壁圆筒的原理，过盈量与配合面径向压力之间的关系如下：

(2)

式中：p为配合面径向压力；ζ为过盈量；d为配合面公称直径；E1为轴承外圈弹性模量；E2为行星轮弹性模量；C1为轴承外圈刚性系数；C2为行星轮刚性系数。

(3)

式中：d1为轴承的内径；d2为行星轮的外径；v1为轴承的泊松比；v2为行星轮的泊松比。

在有限元计算方面，通过Ansys软件建立三维仿真模型，定义材料参数，施加边界条件，最后获取行星轮内齿面的压力分布。对于两种配合公差对应的四个边界过盈量，将理论值与仿真值获取的配合面压力值对比分析，如图2所示。两种计算结果基本吻合，平均误差为5.74%，因此基于Ansys软件计算的行星轮与轴承过盈配合结果具有很高的可信度。

图2 不同过盈量下配合面压力值Fig.2 Contact pressure of different interference values

2.2 无外载下配合面变形分析

在风机实际运行工况下，行星轮系失效破坏的源头是行星轮内孔面，而微动或打滑又是导致其失效的直接原因，因此需首要分析不同配合公差条件下的配合面变形特性。弹性模量正是反映材料抵抗弹性变形能力的指标，行星轮的弹性模量较轴承的弹性模量小，因此当两者过盈配合时，行星轮相对而言是“软材料”，更易变形磨损。通过Ansys仿真计算行星轮内孔与轴承外圈在不同过盈量下的变形量，如图3所示。在总体变形云图中，δ齿轮内表面+δ轴承面=ζ过盈量，而且统计分析发现，行星轮内孔面的变形量占比约为89.5%，轴承外圈的变形量占比约为10.5%，如图4所示，这也定量描述了行星轮相较于轴承的变形程度，更易出现损伤。

(a) 过盈量0.012 mm(P6)

(b) 过盈量0.079 mm(P6)

(c) 过盈量0.054 mm(R6)

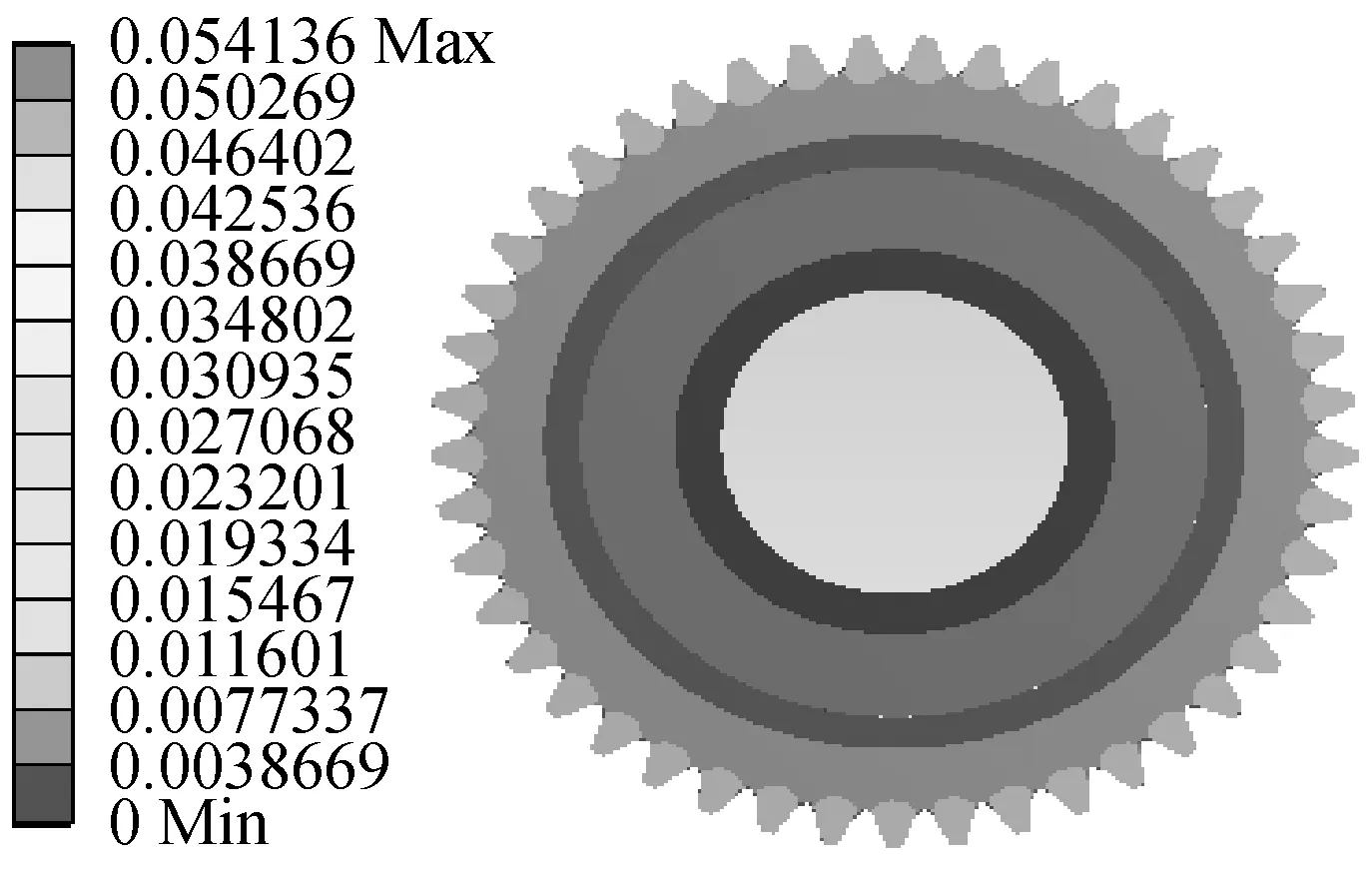
(d) 过盈量0.121 mm(R6)

3 稳定外载下过盈配合接触特性分析

在载荷层面，基于理论计算，额定工况下行星轮配合面处载荷值F=92.9 kN，而实际运行工况下，行星轮所承受的极端载荷约为2.5F～3F。在几何参数方面，分别对两种配合公差P6和R6、四种过盈量值0.012 mm、0.079 mm、0.054 mm、0.121 mm进行接触特性分析。

图4 不同过盈量下配合面变形量占比统计Fig.4 Deformation statistics of different interference values

将仿真获取的行星轮内孔表面滑移参数从Ansys中提取，并在Matlab中数据处理，图5是行星轮内表面的微动滑移量云图，其中颜色深浅与实际微动滑移距离成比例对应。

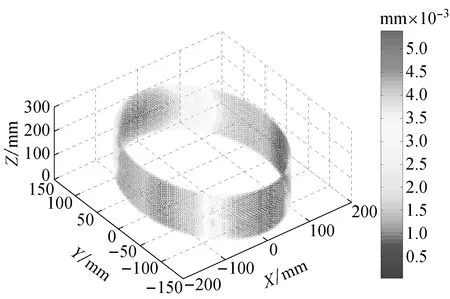
图5 行星轮内表面微动量云图Fig.5 Internal surface’s micro distance of planet gear

基于图5，可获取不同载荷条件(1.0F、1.5F、2.0F、2.5F、3.0F)和不同过盈条件(0.012 mm、0.079 mm、0.054 mm、0.012 mm)下的行星轮内孔与轴承外圈微动滑移量系列图，如图6所示。为进一步比较相对滑移特性，即载荷增大对微动量的影响，将图6的各个曲线与1.0F下的微动量做差后得到曲线，见图7。

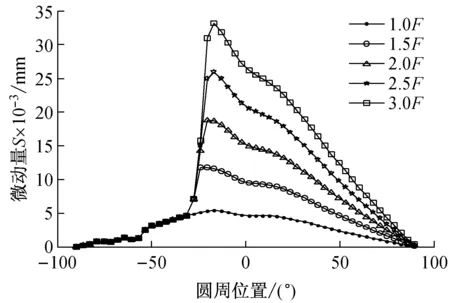
(a) 过盈量0.012 mm(P6)

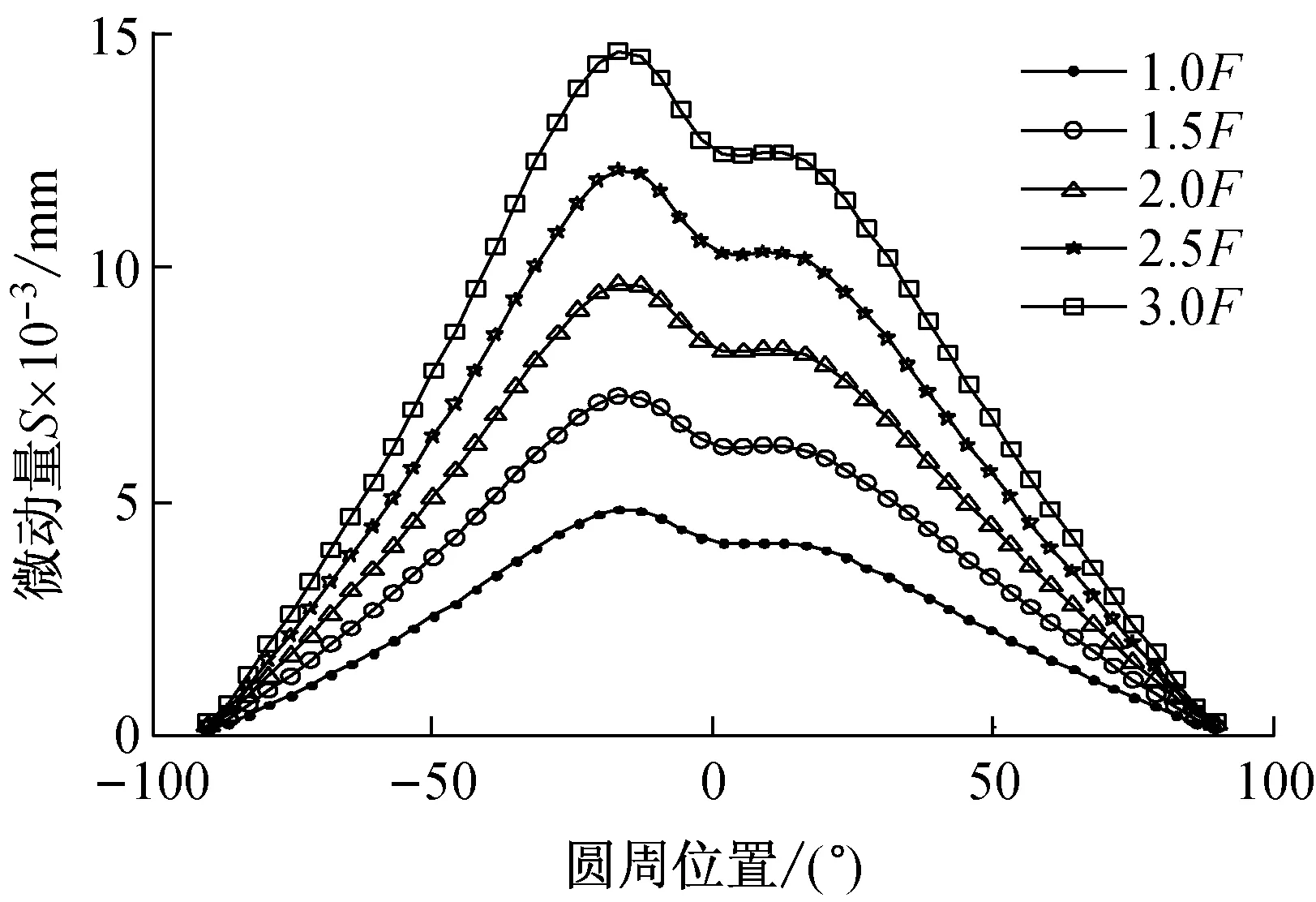
(b) 过盈量0.079 mm(P6)

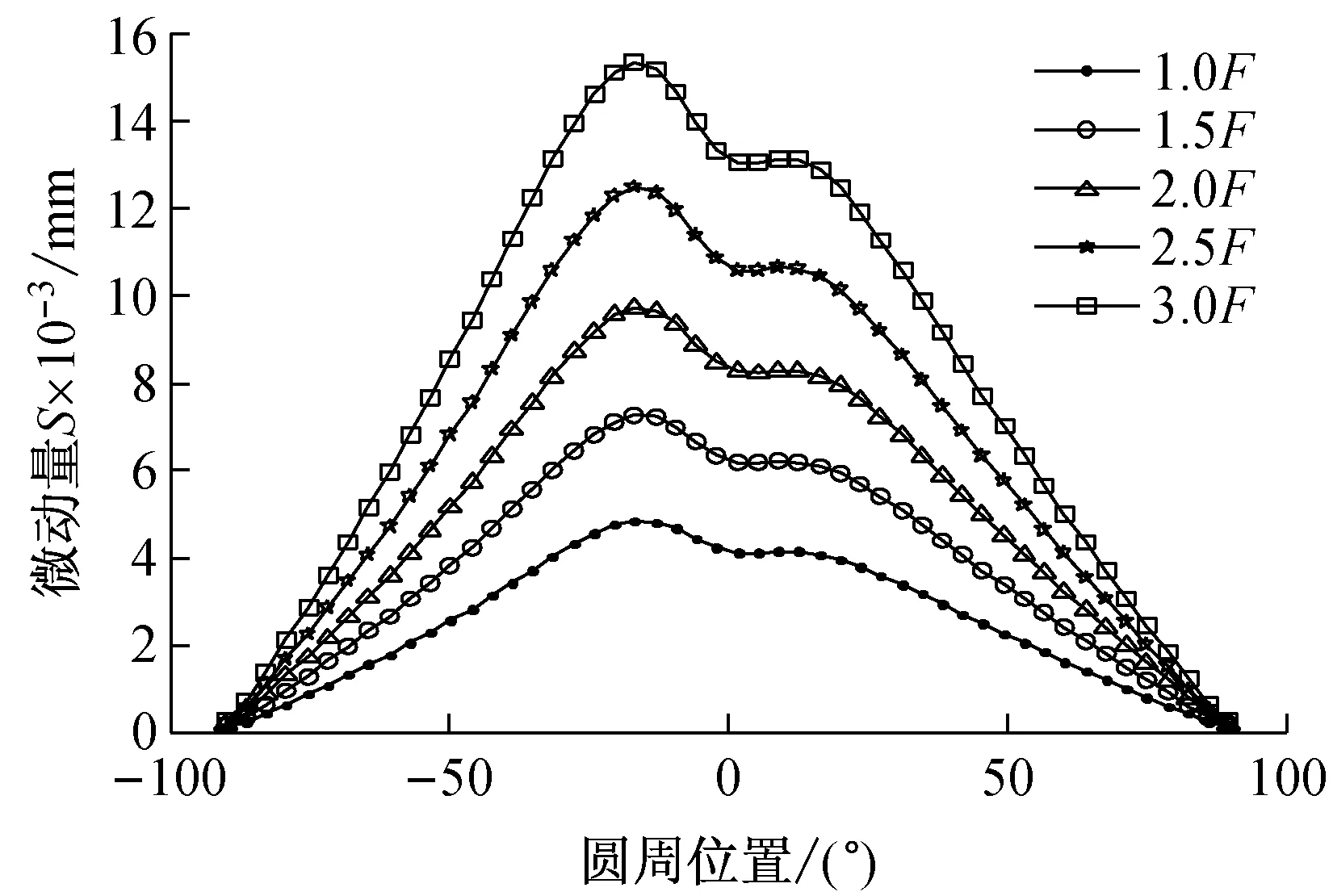
(c) 过盈量0.054 mm(R6)

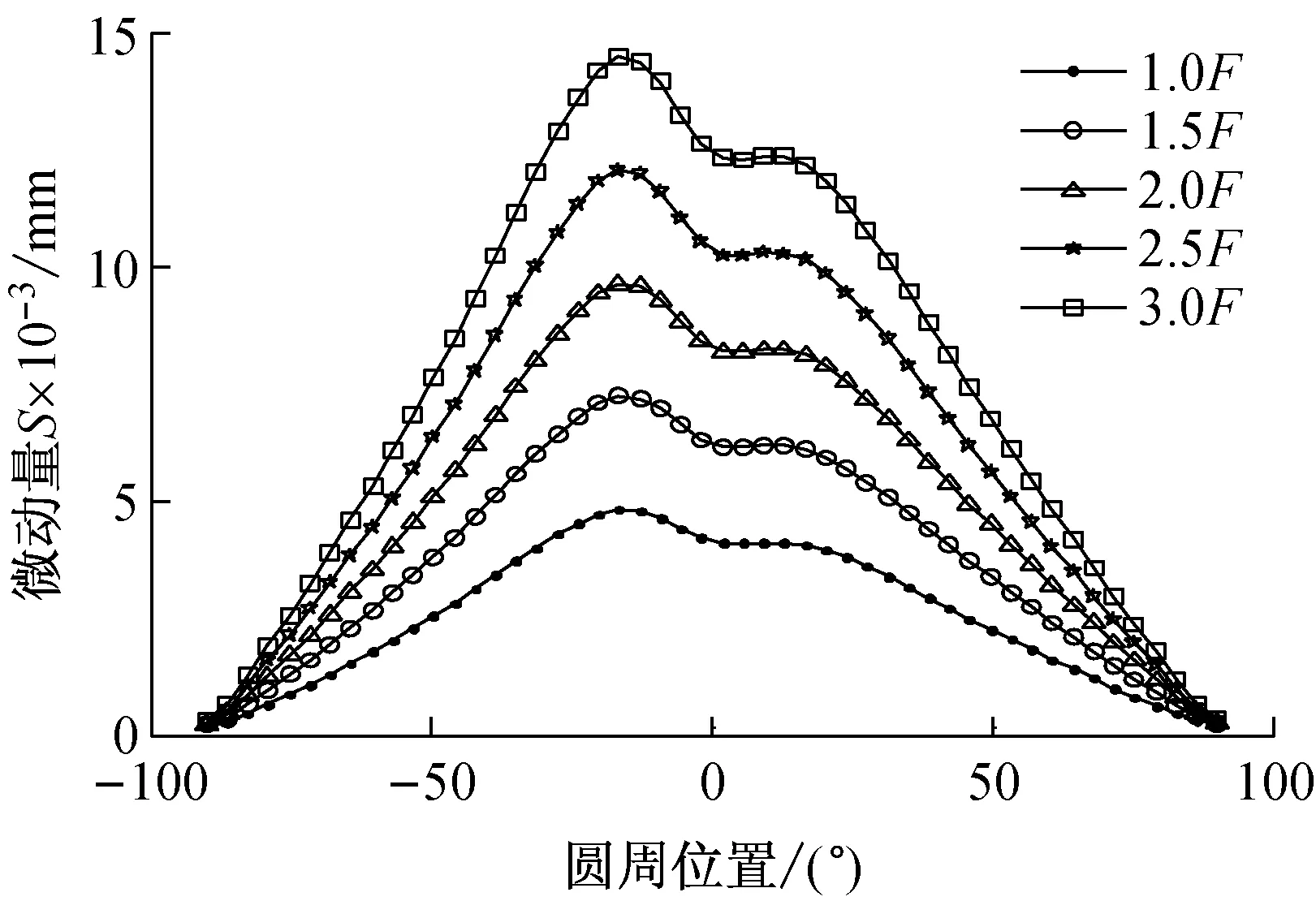
(d) 过盈量0.121 mm(R6)

基于图7的相对微动量对比分析结果，可获取不同配合公差下最大微动量与载荷的关系，如图8所示，行星轮内孔与轴承外圈配合面的最大滑移距离随着载荷递增而增大。针对于配合公差P6的两个极限值，过盈量0.012 mm相对于过盈量0.079 mm，最大滑移距离与载荷关系曲线相差较大，即整个公差带下的最大滑移距离变化幅度很大。然而针对配合公差R6的两个极限值，过盈量0.054 mm相对于过盈量0.121 mm，最大滑移距离与载荷关系曲线相差较小，即整个公差带下的最大滑移距离变化幅度很小，因此风电行星轮系选用R6配合公差更合适。

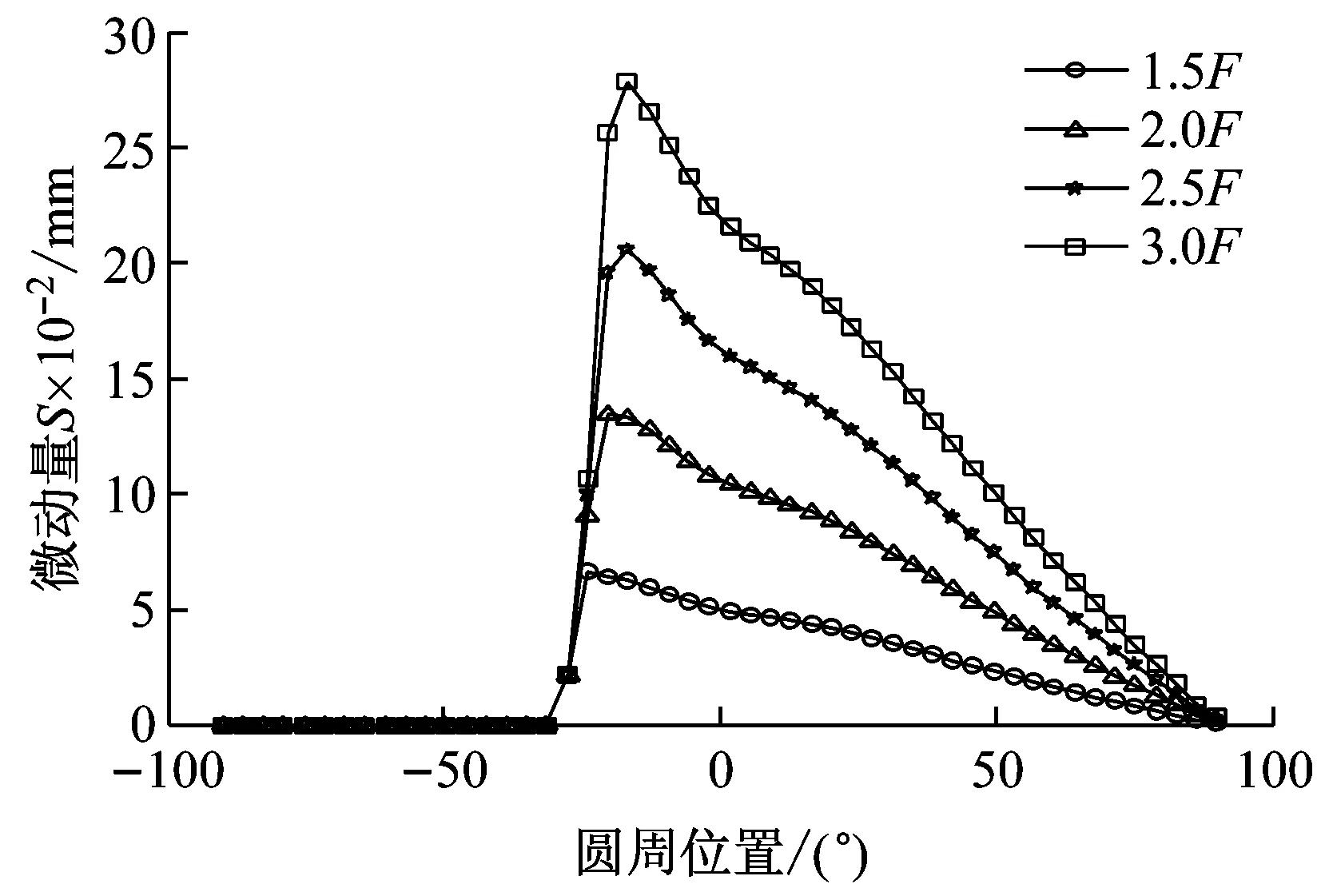
(a) 过盈量0.012 mm(P6)

(b) 过盈量0.079 mm(P6)

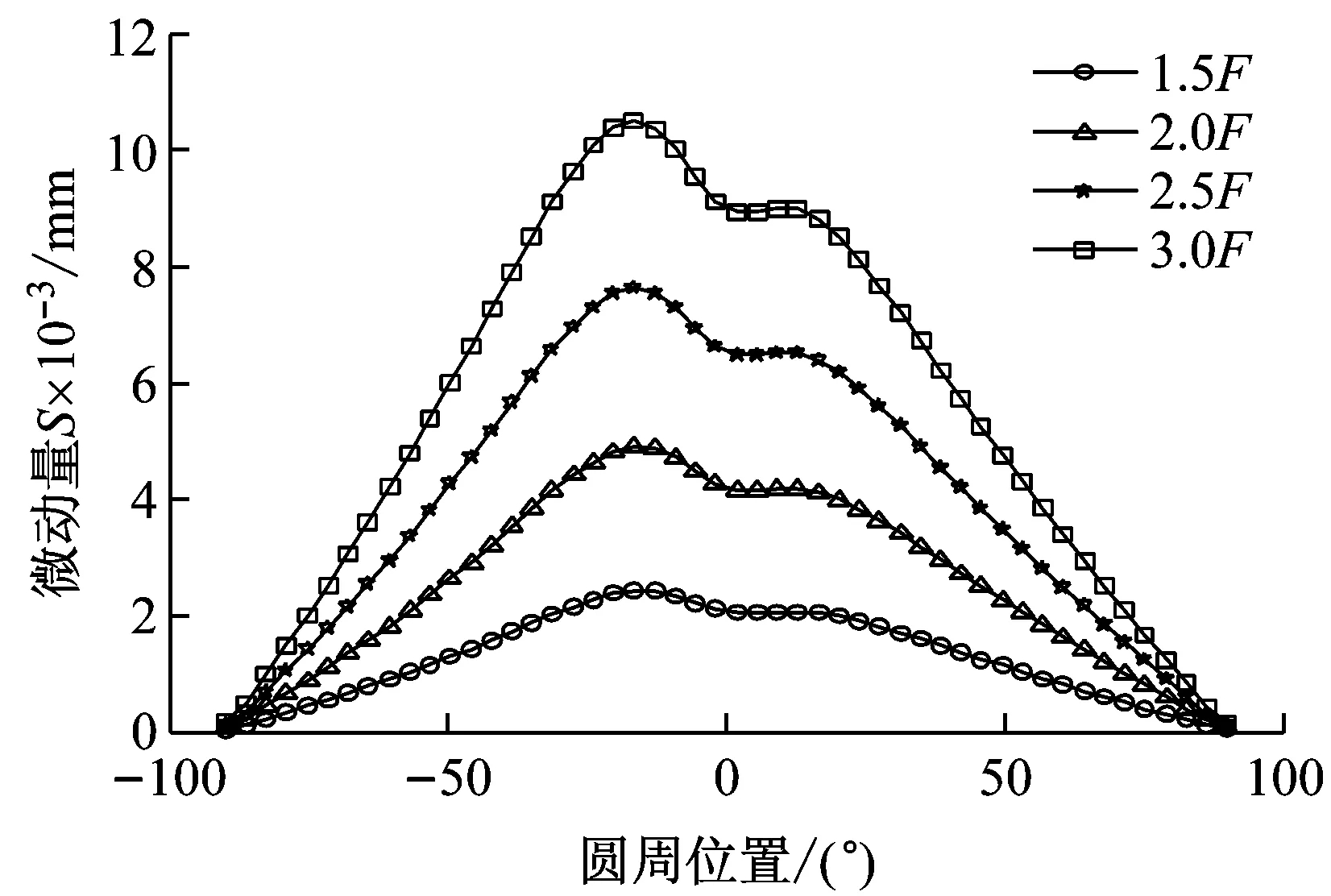
(c) 过盈量0.054 mm(R6)

(d) 过盈量0.121mm(R6)

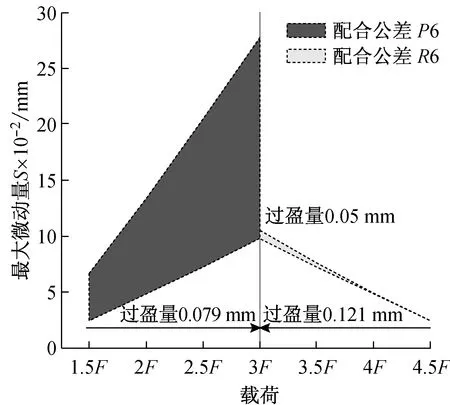
图8 不同配合公差下最大微动量与载荷关系Fig.8 The relation between max micro distance and steady load of different fit tolerance zone

4 非稳态外载下过盈配合接触分析

基于图1的行星轮受力分析与图9的行星轮过盈打滑分析，行星轮内孔与轴承外圈配合面不打滑的条件是：

(4)

式中：ΔT为行星轮两端所受扭矩瞬时差值；Tf为配合面的摩擦阻力矩；Fu为配合面摩擦力。

将式(4)展开，且配合面摩擦力采用圆周数值积分方法获取，可得：

(5)

(6)

式中：ΔFn为行星轮两端所受作用力差值；D为行星轮分度圆直径；α为压力角；u为摩擦因数；B为齿宽。

图9 非稳态载荷下过盈打滑分析Fig.9 Interference sliding analysis of unsteady load

最终计算获取不同过盈量下的打滑极限载荷差ΔFn，如图10所示。可为齿轮箱设计提供一定参考。

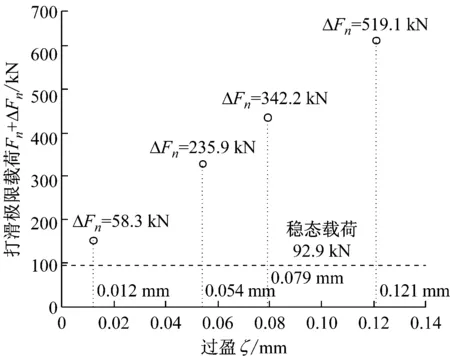
图10 不同过盈量的打滑极限载荷Fig.10 Sliding ultimate load of different interference values

5 结 论

(1) 通过对比不同过盈量在无外载工况下的配合面压力值，采用厚壁圆筒理论计算结果和基于有限元仿真计算结果的平均误差为5.74%，说明基于Ansys开展过盈分析具有较高可信度。

(2) 通过对比不同过盈量在无外载工况下的变形量值，可以发现，行星轮内孔面的变形量占比约为89.5%，轴承外圈的变形量占比约为10.5%，定量地描述了行星轮相较于轴承的变形程度，更易出现损伤。

(3) 稳态工况下，行星轮所承受载荷增大时，在配合面受力位置附近会出现微动滑移。通过对比不同配合公差P6和R6下的最大微动量，R6公差带下最大微动量随载荷变化幅度相对不明显，因此风电行星轮配合公差选择R6更合适。

(4) 非稳态工况下，通过数值积分计算获取不同过盈量下的配合面打滑极限载荷。在实际服役条件下，若行星轮两端所受载荷差值超出该极限值，配合面不仅限于“微动滑移”，而是出现剧烈“打滑现象”。

[1] TRUMAN C E, BOOKER J D.Analysis of a shrink-fit failure on a gear hub/shaft assembly[J].Engineering Failure Analysis, 2007,14(4):557-572.

[2] JUUMA T.Torsional fretting fatigue strength of a shrink-fitted shaft with a grooved hub[J].Tribology International, 2000,33(8):537-543.

[3] GUTKIN R, ALFREDSSON B.Growth of fretting fatigue cracks in a shrink-fitted joint subjected to rotating bending[J].Engineering Failure Analysis, 2008,15(5):582-596.

[4] JAFRI S M M A, VANCE J M B.Shrink fit effects on rotordynamic stability: Theoretical study[Z].Berlin: 2008，5：1017-1024.

[5] LEE D H, KWON S J, YOU W H.Characteristics of fretting wear in a press-fitted shaft subjected to bending load[J].Advanced Materials Research, 2010,97/98/99/100/101:1269-1272.

[6] LANOUE F, VADEAN A, SANSCHAGRIN B.Fretting fatigue strength reduction factor for interference fits[J].Simulation Modelling Practice and Theory, 2011,19(9):1811-1823.

[7] LANOUE F, VADEAN A, SANSCHAGRIN B.Finite element analysis and contact modelling considerations of interference fits for fretting fatigue strength calculations[J].Simulation Modelling Practice and Theory, 2009,17(10):1587-1602.

[8] PAREDES M, NEFISSI N, SARTOR M.Study of an interference fit fastener assembly by finite element modelling, analysis and experiment[J].International Journal on Interactive Design and Manufacturing (IJIDeM), 2012,6(3):171-177.

[9] ALFREDSSON B.Fretting fatigue of a shrink-fit pin subjected to rotating bending: Experiments and simulations[J].International Journal of Fatigue, 2009,31(10):1559-1570.

[10] CROCCOLO D, DE AGOSTINIS M, FINI S, et al.Analysis of the influence of fretting on the fatigue life of interference fitted joints[Z].American Society of Mechanical Engineers (ASME), 2014: 2B.

[11] ZENG F, CAI Z, FENG Z, et al.In situ observation and analysis of a shrink-fitted PMMA shaft subjected to rotating bending[J].Tribology International, 2012,48:149-154.

[12] BERTINI L, SANTUS C.Fretting fatigue tests on shrink-fit specimens and investigations into the strength enhancement induced by deep rolling[J].International Journal of Fatigue, 2015,81:179-190.

Interference contact characteristics of planetary gear train for wind turbines

XIANG Dong, SHEN Gang, ZHU Kan, SHEN Yinhua, JIANG Li

(Department of Mechanical Engineering, Tsinghua University, Beijing 100084, China)

Wind power generation has a great significance for ensuring our country’s energy sources security, but there still is a huge technical bottleneck.So, how to further improve wind turbine’s reliability and service life is an urgent problem to be solved.Here, the relationship between the contact characteristics of interference fitting surfaces and fretting wear was taken as a break through point, and the load boundary conditions were calculated based on the stress analysis of NGW type planetary gear.By comparing stress values of a fitting surface under the conditions of different interferences and no external load, it was shown that the average error between the theoretical calculation and simulation analysis is about 5.74%, it verifies the reliability of the simulation; through comparing the deformation quantities of the fitting surface under the conditions of different interferences and no external load, the deformations of the planetary gear inner hole surface and the bearing outer ring occupy 89.5% and 10.5%, respectively; so, the planetary gear is easier to be damaged than the bearing be; through comparing the maximum fretting slips under the conditions ofP6 andR6 fitting tolerances and steady state load, the maximum fretting slip ofP6 varies greatly with the load variation and that ofR6 is more suitable to planetary gear tolerance; with numerical integration under the condition of non-steady state load, the slip limit loads of the fitting surface under different interferences are calculated, and there limit values should be considered in the design, because these limit values are taken as a criterion to evaluate the severe “slipping phenomenon” in actual service conditions.

wind turbine; interference fit; fit tolerance; fretting slip; slipping phenomenon

国家自然科学基金(51475263)

2015-12-07 修改稿收到日期：2016-02-18

向东 男，副教授，博士生导师，1972年生

沈岗 男，博士生，1989年生

TH113

A

10.13465/j.cnki.jvs.2017.05.004