基于Hoek-Brown准则的混凝土-岩石类靶侵彻模型
2017-04-08曹扬悦也蒋志刚谭清华蒙朝美
曹扬悦也,蒋志刚,谭清华,蒙朝美
(国防科学技术大学 指挥军官基础教育学院,长沙 410072)
基于Hoek-Brown准则的混凝土-岩石类靶侵彻模型
曹扬悦也,蒋志刚,谭清华,蒙朝美
(国防科学技术大学 指挥军官基础教育学院,长沙 410072)
基于空腔膨胀理论建立工程模型是研究侵彻问题的常用方法。针对射弹侵彻岩石-混凝土类脆性材料半无限靶问题,基于靶体的弹性-裂纹-粉碎响应模式,粉碎区采用考虑围压的Hoek-Brown准则,得到了准静态球形空腔膨胀的空腔壁压力。在Forrestal两个阶段侵彻模型中,用所得空腔壁压力代替隧道侵彻阶段的侵彻阻力,得到刚性弹侵彻岩石-混凝土类脆性材料半无限靶的侵彻深度预估公式,与文献侵彻试验以及现有典型侵彻深度预估公式比较表明,预估公式适用范围更广,对于(超)高强混凝土和岩石材料靶的预测精度更高。
侵彻;混凝土-岩石靶;工程模型;空腔膨胀;Hoek-Brown准则
射弹侵彻混凝土-岩石类材料问题一直是防护工程领域的研究热点,已有众多经验公式[1-3]和理论模型[4],其中基于空腔膨胀理论的侵彻模型得到了大量研究。FORRESTAL及其合作者[5-7]基于侵彻试验和空腔膨胀理论,将侵彻过程分为开坑和隧道侵彻两个阶段,建立了卵形头刚性弹侵彻混凝土的半理论公式,LI等[8-9]将其拓展到了任意弹头形状。FORRESTAL等[10]针对混凝土靶的塑性(粉碎)-弹性和塑性(粉碎)-裂纹-弹性两种响应模式,采用Mohr-Coulomb准则,建立了混凝土为不可压缩和可压缩材料的动态球形空腔膨胀理论,并采用数值方法求解可压缩材料空腔膨胀模型,拟合得到了空腔壁压力的无量纲表达式。李志康等[11-14]进一步考虑粉碎区的孔隙压实效应,建立了密实-孔隙压实-裂纹-弹性响应的准静态和动态球形空腔膨胀理论。HE等[15-16]考虑粉碎区的剪胀性,建立了动态球形和柱形空腔膨胀理论。黄民荣等[17]采用Griffith强度准则,建立了粉碎-裂纹-弹性响应的球形、柱形空腔膨胀模型和卵形头刚性弹侵彻深度公式。最近,FENG等[18]考虑应变率效应,采用修正的Drucker-Prager帽盖模型,建立了密实-孔隙压实-裂纹-弹性响应的动态球形空腔膨胀理论。彭永等[19]基于Mohr-Coulomb准则的可压缩材料动态球形空腔膨胀模型,分析了混凝土强度、弹性模量、泊松比和压力硬化系数等参数对侵彻阻力的影响,结果表明:混凝土强度和弹性模量的影响明显,而泊松比和压力硬化系数的影响很小。侵彻试验[20-22]表明,岩石的侵彻效应与混凝土类似。但是,硬质岩石的强度较高,脆性大于混凝土,目前有关岩石侵彻深度经验公式[23]和侵彻模型研究[24-26]均较少。
试验和理论研究表明:① 常规弹速射弹侵彻混凝土-岩石类材料半无限靶的过程可分为开坑和隧道侵彻两个阶段,隧道侵彻阶段的侵彻阻力可采用粉碎-裂纹-弹性响应的球形空腔膨胀模型解。② 在隧道侵彻阶段,粉碎区处于三向受压状态,其本构模型对侵彻深度公式的精度和求解复杂性影响较大。为了得到空腔壁压力的解析解,通常忽略粉碎区材料的压缩性、剪胀性和应变率效应等,并采用简单的强度准则(Mohr-Coulomb强度准则和Griffith强度准则),但所得侵彻深度公式具有局限性;若考虑粉碎区的压缩性、剪胀性或应变率效应,则计算十分复杂,需采用数值方法求解非线性微分方程。③ Forrestal半理论公式及其拓展形式(Li和Chen公式)计算简单,对单轴抗压强度较低的混凝土靶预测精度较好,但对于高强(单轴抗压强度σu大于50 MPa)和超高强(单轴抗压强度σu大于100 MPa)的混凝土和岩石靶体的适用性较差。
为了建立计算简便、适用范围较广,可用于超高强混凝土和高强度岩石的侵彻深度公式,本文基于弹性-裂纹-粉碎响应模式,针对粉碎区为三向受压的特点,首次采用考虑围压影响的Hoek-Brown准则[27-29]描述粉碎区的强度特性,通过求解准静态球形空腔膨胀模型,得到了空腔壁压力的解析解;用其代替Forrestal两阶段模型的侵彻阻力,得到了刚性弹侵彻混凝土-岩石类材料靶的侵彻深度公式;最后,与混凝土和岩石侵彻试验进行了比较。
1 基于Hoek-Brown准则的准静态空腔膨胀模型
1.1 Hoek-Brown准则
HOEK等[27]考虑围压对岩体破坏的影响,通过大量的岩石三轴压缩试验,并结合Griffith强度准则,建立了有围压岩体的强度准则,即Hoek-Brown准则:
(1)
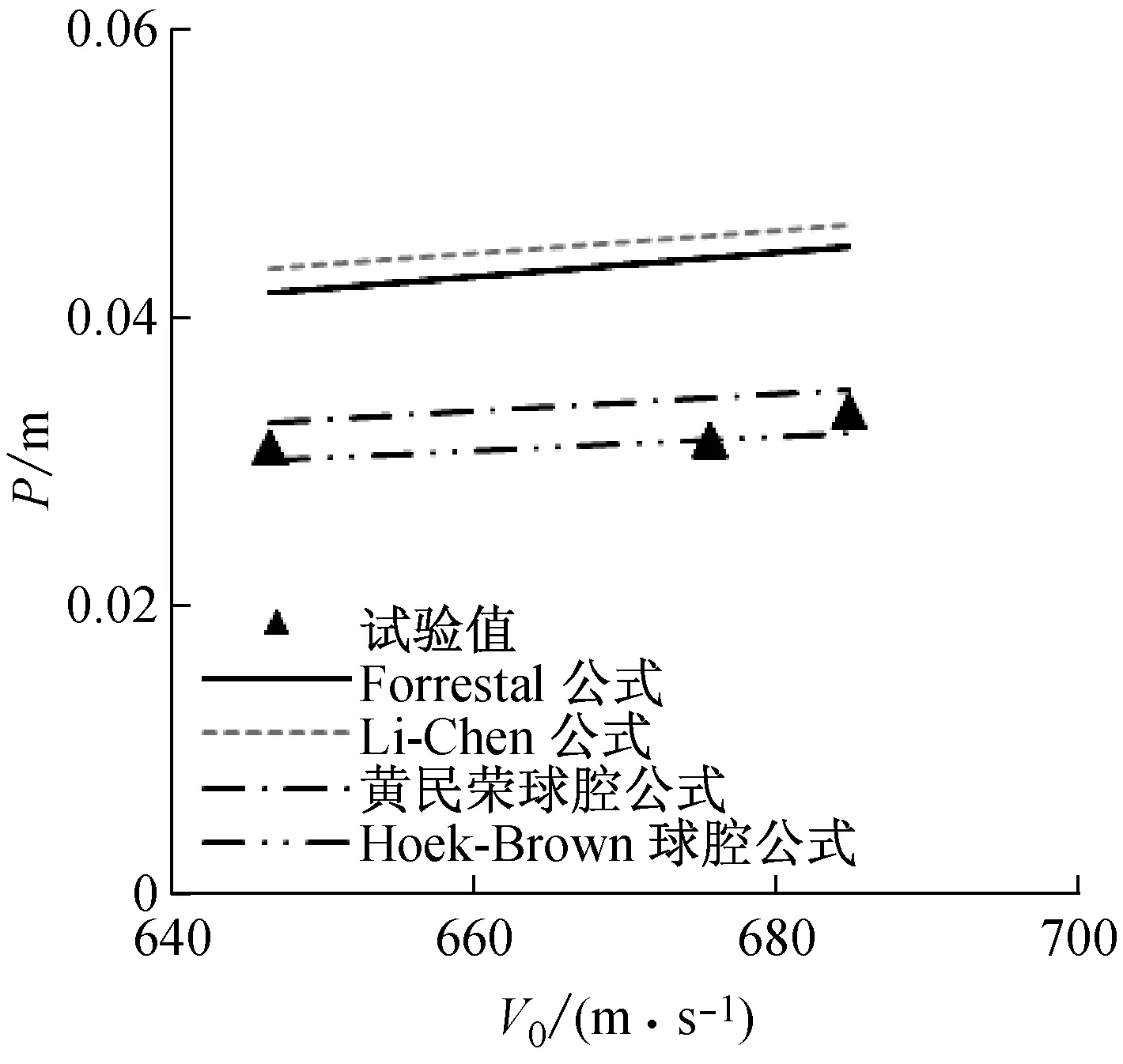
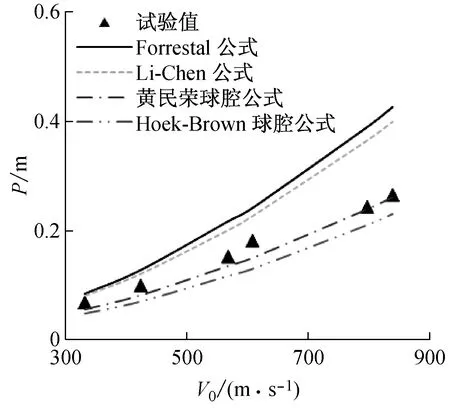
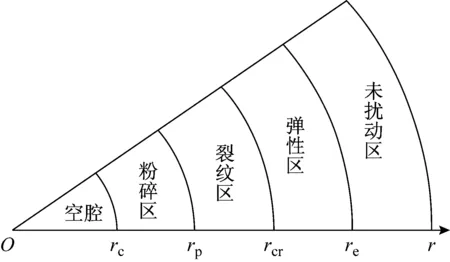
式中:σ1和σ3均以压为正,分别为最大和最小主压应力;σu为材料的单轴抗压强度;m为无量纲经验系数,与材料强度及脆性有关,材料强度及脆性越大,则m取值越大,反之则越小;0 (σ1-σ3)2=σu(mσ3+σu) (2) 根据文献[29],对于混凝土,m的取值范围为5~10;对于岩石,m可近似按以下经验公式计算: (3) 式中,σt为材料的单轴抗拉强度,取绝对值计算。 HOEK等[27-29]指出:Griffith强度准则可反映岩石类材料微裂纹的起裂,但不能反映裂纹的扩展传播和岩体的破坏;Mohr-Coulomb准则可反映岩石类材料的剪切破坏,但由于假设内摩擦角为常数,强度包线为直线,不能反映三向受压状态的破坏特征;Hoek-Brown准则强度包线为曲线,与岩石三向受压试验吻合较好。 混凝土和岩石均为带初始微裂纹的脆性材料,两者力学行为相近,Hoek-Brown准则可推广应用到三向受压混凝土。以文献[30]混凝土三轴受压试验为例,分析比较Mohr-Coulomb、Griffith和Hoek-Brown准则的适用性。试验采用边长为100 mm的立方体试块,混凝土抗压强度σu=35 MPa,抗拉强度σt=5.5 MPa,极限状态的最大、最小主压应力σ1、σ3关系如图1所示。其中:m=5~10曲线为Hoek-Brown准则式(2)的结果;Mohr-Coulomb准则曲线按文献[10]公式计算,取压力硬化系数λ=0.69(根据文献[19],σu=30~150 MPa时,λ=0.62~0.75,平均值为0.69);Griffith准则曲线按文献[17]公式计算。 图1 三种屈服准则与试验结果比较Fig.1 Comparison of yield criterions and test results 由图1可知:① Mohr-Coulomb和Griffith准则与试验偏差较大,均小于试验结果,最大误差分别达到27%和24%左右。② Hoek-Brown准则取m=5~10时,与试验吻合较好,这与文献[29]一致。其中:σ3值较小时(小于约0.5σu),可取m=5~7,最大误差约为14%;σ3值较大时(大于约0.5σu),可取m=8~10,最大误差约为8%。 以上分析表明:Hoek-Brown准则比Mohr-Coulomb和Griffith强度准则更符合混凝土-岩石类材料三向受压的强度特点;在侵彻问题中,粉碎区处于三向受压状态,采用Hoek-Brown准则更合适。 1.2 准静态球形空腔膨胀的空腔壁压力 设一球形空腔在混凝土-岩石类无限介质中以很低的速度均匀膨胀,则准静态空腔膨胀模型,如图2所示。响应区包括粉碎区、径向裂纹区和弹性区。其中,rc、rp、rcr和re分别为空腔半径、粉碎区外半径、裂纹区外半径和弹性区外半径,r为球面径向坐标。采用以下基本假定:粉碎区服从Hoek-Brown准则;裂纹区环向应力恒为0,处于径向受压状态;弹性区为小应变,服从广义虎克定律,材料弹性模量为E,泊松比为υ。 图2 准静态空腔膨胀模型Fig.2 Static cavity expansion mode 对于准静态球形空腔膨胀,响应区的平衡方程为 (4) 式中:σr为径向应力;σθ为环向应力,均以受压为正。 弹性区(rcr≤r≤re),由广义虎克定律、边界条件(r=re,σr=0)和环向拉伸断裂条件(r=rcr,σθ=-σt),可得应力场和位移场[31]: (5) (6) (7) 裂纹区(rp≤r≤rcr),将σθ=0代入平衡方程式(4),并考虑裂纹区与粉碎区交界处的强度条件(r=rp,σr=σu)和径向位移连续条件,可得[31]: (8) (9) 粉碎区(rc≤r≤rp),应力满足Hoek-Brown准则,即式(2)。取σr=σ1﹥σθ=σ3,由式(2),有: (10) (11) 解之得: (12) 式中:c0为积分常数,可由裂纹区与粉碎区交界处径向应力连续条件(r=rp,σr=σu)求得: (13) 将c0代入式(12),得到求解粉碎区径向应力的方程: (14) 式中:粉碎区外半径rp未知,需确定其与空腔半径rc的关系。 考r=rcr虑的径向应力连续条件,可得半径rp与rcr的关系: (15) 类似于文献[31],忽略粉碎区材料密度的变化和粉碎区外边界位移的高阶项,由粉碎区的质量守恒以及r=rp处的位移连续条件,有: (16) 对于准静态空腔膨胀,令re→∞,由式(15)得: (17) 由式(16)得: 赵集手忙脚乱,说:“做做,今儿喝肉汤的人多。”从筐里拎出几根猪腿棒子,搁墩案上,举起斧头,砰、砰砍,骨渣飞溅。 (18) 将式(17)、(18)代入式(14),并取r=rc,σr=σrc,得到求解空腔壁压力σrc的方程: (19) 2.1 现有典型公式 Forrestal公式[5-7](卵形弹头): (20a) (20b) 式中:P为侵彻深度;M和a分别为弹丸的质量和半径;V0为弹丸撞击速度;ρc为靶体材料密度;R=sfc,经验常数S=82.6(fc/10-6)-0.544,其中fc为单轴抗压强度σu(Pa);卵形弹头(曲径比Ψ)的形状系数N*为 (20c) Li-Chen公式[8-9](任意形状弹头): (21a) (21b) 式中:侵彻深度较大时取k=1.5~2.5,侵彻深度较小时取k=0.707+h/d,其中h为弹头长度,d=2a为弹径;经验常数S=72(fc/10-6)-0.5;弹头形状系数N*参见文献[8];其余符号含义同Forrestal公式。 2.2 基于Hoek-Brown准则公式 在Forrestal公式中取R=σrc,得基于Hoek-Brown准则和准静态球形空腔膨胀的侵彻深度公式: (22a) (22b) 式中:σrc为由式(19)解得的空腔壁压力;任意弹头的形状系数N*按Li-Chen公式[8],其余参数含义同前。 选取典型的卵形头刚性弹侵彻混凝土和岩石半无限靶试验进行计算,弹、靶特征参数及来源,如表1所示。 表1 侵彻试验参数Tab.1 Parameters of the Penetration Tests 由图3和图4可知: (1) Forrestal公式和Li-Chen公式的计算结果基本一致,对于σu小于或接近50 MPa的普通混凝土靶,计算结果与试验吻合较好,其中例1和例2的最大误差分别不超过16%和22%。但是,对于(超)高强混凝土和岩石靶(例3-6),由于经验系数S来源于强度较低的普通混凝土靶侵彻试验,外延性较差,而(超)高强混凝土和岩石的强度和脆性均比普通混凝土大,经验系数S已不适用,因此侵彻深度计算结果明显偏大。 (2) 黄民荣球腔公式基于Griffith强度准则和球形空腔模型,例1-5侵彻深度计算结果均大于试验,最大误差分别约为26.0%、17.2%、16.7%、9.3%和25.9%。由于Griffith强度准则不能反映其在三向受压状态下的破坏,基于Griffith强度准则球形空腔模型的空腔壁压力偏小,因此黄民荣球腔公式的例1-5计算结果大于试验。需指出,例6由于试验靶体不是半无限靶,因此黄民荣球腔公式结果小于试验。 (3) 本文Hoek-Brown球腔公式计算不同强度混凝土和岩石靶侵彻深度的结果均与试验吻合较好,其中例1-5的最大误差分别为15.8%、9.9%、5.4%、4.6%和19.2%。需指出,例6由于靶径与弹径比值偏小,不满足半无限靶条件,试验中靶的响应模式为裂纹-粉碎响应[20],且侧向约束不够,导致侵彻阻力小于半无限靶,所以本文Hoek-Brown球腔公式的计算侵彻深度小于试验结果。 总体而言,对于弹速为250~1 600 m/s的刚性弹侵彻强度35~150 MPa的混凝土和岩石靶体问题,本文Hoek-Brown球腔公式具有较高预测精度。 本文采用Hoek-Brown准则描述粉碎区材料的强度特性,得到了空腔壁压力的解析解,并用其代替Forrestal两阶段模型的侵彻阻力,建立了刚性弹侵彻混凝土-岩石类材料靶的侵彻深度公式。与混凝土和岩石半无限靶侵彻试验比较,表明: (1) Forrestal公式和Li-Chen公式适用于刚性弹侵彻普通混凝土半无限靶的侵彻深度,但不适用于(超)高强混凝土和岩石靶;黄民荣基于Griffith强度准则球腔公式侵彻深度计算结果偏大。 (a) 例1(编号1,混凝土,σu=36.0 MPa) (b) 例2(编号2,混凝土,σu=51.0 MPa) (c) 例3(编号3,混凝土,σu=87.8 MPa) (d) 例4(编号4,混凝土,σu=150.9 MPa) (a) 例5(编号5,岩石,σu=60.0 MPa) (b) 例6(编号6,岩石,σu=154.0 MPa) (2) 本文基于Hoek-Brown准则球腔公式适用范围较广,精度较高,并能较好地预测刚性弹侵彻(超)高强混凝土和岩石半无限靶的侵彻深度。 [1] HEUZE F E.An overview of projectile penetration into geological materials, with emphasis on rock[J].Int J Rock Mechanics and Mining Sciences and Geomechanics Abstracts, 1990, 27(1):1-14. [2] LI Q M, REID S R, WEN H M.Local impact effects of hard missiles on concrete targets[J].Int J Impact Eng., 2005, 32: 224-284. [3] RANJAN R, BANERJEE S, SINGH R K, et al.Local impact effects on concrete target due to missile: An empirical and numerical approach[J].Annals of Nuclear Energy, 2014, 68: 262-275. [4] BEN-DOR G, DUBINSKY A, ELPERIN T.Analytical engineering models for predicting high speed penetration of hard projectiles into concrete shields: A review[J].Int J Damage Mechanics, 2015, 24(1): 76-94. [5] FORRESTAL M J, ALTAN B S, CARGILE D, et al.An empirical equation for penetration depth of ogive-nose projectile into concrete targets[J].Int.J.Impact Eng., 1994, 15: 395-405. [6] FORRESTAL M J, FREW D J, HANCHAK S J, et al.Penetration of grout and concrete targets with ogive-nose steel projectiles[J].Int J Impact Eng., 1996, 18: 465-476. [7] FREW DJ, HANCHAK S J, GREEN M L, et al.Penetration of concrete targets with ogvie-nose steel rods[J].Int.J.Impact Eng., 1998, 21: 489-497. [8] CHEN X W, LI Q M.Deep penetration of a non-deformable projectile with different geometrical characteristics[J].Int.J.Impact Eng., 2002, 27: 619-637. [9] LI Q M, CHEN X W.Dimensionless formula for penetration depth of concrete target impacted by a non-deformable projectile[J].Int.J.Impact Eng., 2003, 28: 93-116. [10] FORRESTAL M J, TZOU D Y.A spherical cavity-expansion penetration model for concrete targets[J].Int J Solids and Structures, 1997, 34(31/32): 4127-4146. [11] 李志康, 黄风雷.考虑混凝土孔隙压实效应的球形空腔膨胀理论[J].岩土力学, 2010, 31(5): 1481-1485. LI Zhikang, HUANG Fenglei.A spherical cavity expansion theory of concrete considering voids compacted effects[J].Rock and Soil Mechanics, 2010, 31(5): 1481-1485. [12] 李志康, 黄风雷.高速杆弹侵彻半无限混凝土靶的理论分析[J].北京理工大学学报,2010,30(1): 10-13. LI Zhikang, HUANG Fenglei.High velocity long rod projectile’s penetration into semi-infinite concrete targets[J].Transactions of Beijing Institute of Technology, 2010,30(1): 10-13. [13] 郭香华, 张庆明, 何远航.弹体正侵彻混凝土厚靶的运动规律理论研究[J].北京理工大学学报, 2011, 31(3): 269-271, 293. GUO Xianghua, ZHANG Qingming, HE Yuanhang.Study on kinematics properties of projectile normal penetration into semi-infinite concrete targets[J].Transactions of Beijing Institute of Technology, 2011, 31(3): 269-271, 293. [14] 郭香华, 张庆明, 何远航.混凝土厚靶在弹体正侵彻下的响应研究[J].北京理工大学学报, 2011, 31(7): 765-767. GUO Xianghua, ZHANG Qingming, HE Yuanhang.Study on behavior of semi-infinite concrete targets subjected to projectile normal penetration[J].Transactions of Beijing Institute of Technology, 2011, 31(7): 765-767. [15] HE T, WEN H M, GUO X J.A spherical cavity expansion model for penetration of ogival-nosed projectiles into concrete targets with shear-dilatancy[J].Acta Mechanica Sinica, 2011, 27(6): 1001-1012. [16] GUO X J, HE T, WEN H M.Cylindrical cavity expansion penetration model for concrete targets with shear dilatancy[J].Engineering Mechanics, 2012, 139(9): 1260-1267. [17] 黄民荣, 顾晓辉, 高永宏.基于Griffith强度理论的空腔膨胀模型与应用研究[J].力学与实践, 2009, 31(5): 30-34. HUANG Minrong, GU Xiaohui, GAO Yonghong.Cavity expansion model based on the Griffith strength theory and its application[J].Mechanics in Engineering, 2009, 31(5): 30-34. [18] FENG J, LI W, WANG X M, et al.Dynamic spherical cavity expansion analysis of rate-dependent concrete material with scale effect[J].Int.J.Impact Eng., 2015, 84: 24-37. [19] 彭永, 方秦, 吴昊,等.对弹体侵彻混凝土靶体阻力函数计算公式的探讨[J].工程力学, 2015, 32(4): 112-119. PENG Yong, FANG Qin, WU Hao, et al.Discussion on the resistance forcing function of projectiles penetrating into concrete targets[J].Engineering Mechanics, 2015, 32(4): 112-119. [20] 张德志, 张向荣, 林俊德,等.高强钢弹对花岗岩正侵彻的试验研究[J].岩石力学与工程学报, 2005, 24(9): 1612-1618. ZHANG Dezhi, ZHANG Xiangrong, LIN Junde, et al.Penetration experiments for normal impact into granite targets with high-strength steel projectile[J].Chinese Journal of Rock Mechanics and Engineering, 2005, 24(9): 1612-1618. [21] 沈俊, 徐翔云, 何翔,等.弹体高速侵彻岩石效应试验研究[J].岩石力学与工程学报, 2010, 29(2): 4207-4212. SHEN Jun, XU Xiangyun, HE Xiang, et al.Experimental study of effect of rock targets penetrated by high-velocity projectiles[J].Chinese Journal of Rock Mechanics and Engineering, 2010, 29: 4207-4212. [22] 王海兵, 寿列枫, 张建鑫,等.弹丸撞击下花岗岩靶破坏效应试验与数值分析[J].岩石力学与工程学报, 2014, 32(2): 366-375. WANG Haibing, SHOU Liefeng, ZHANG Jianxin, et al.Experiments and numerical analysis of destructive effects of granite target under impact of projectile[J].Chinese Journal of Rock Mechanics and Engineering, 2014, 32(2): 366-375. [23] 张德志, 林俊德, 唐润棣,等.高强度岩石侵彻经验公式[J].兵工学报, 2006, 27(7):15-18. ZHANG Dezhi, LIN Junde, TANG Rundi, et al.An empirical equation for penetration depth of projectiles into high-strength rock targets[J].ACTA Armamentarii, 2006, 27(7):15-18. [24] 王明洋, 谭可可, 吴华杰,等.钻地弹侵彻岩石深度计算新原理与方法[J].岩石力学与工程学报, 2009, 28(9): 1863-1869. WANG Mingyang, TAN Keke, WU Huajie, et al.New method of calculation of projectile penetration into rock[J].Chinese Journal of Rock Mechanics and Engineering, 2009, 28(9): 1863-1869. [25] 吴昊, 方秦, 龚自明,等.应用改进的双剪强度理论分析岩石靶体的弹体侵彻深度[J].工程力学, 2009, 26(8):216-222. WU Hao, FANG Qin, GONG Ziming, et al.Analysis on penetration depth of projectiles into rock targets based on the improved twin shear strength theory[J].Engineering Mechanics, 2009, 26(8): 216-222. [26] 吴昊, 方秦, 龚自明.考虑刚性弹弹头形状的混凝土(岩石)靶体侵彻深度半理论分析[J].爆炸与冲击, 2012, 32(6): 573-580. WU Hao, FANG Qin, GONG Ziming.Semi-theoretical analysis for penetration depth of rigid projectiles with different nose geometries into concrete (rock) targets[J].Explosion and Shock Waves, 2012, 32(6): 573-580. [27] HOEK E, BROWN E T.Empirical strength criterion for rock masses[J].Journal of the Geotechnical Engineering Division (ASCE), 1980, 106(9): 1013-1035. [28] HOEK E.Strength of jointed rock masses[J].Geotechnique, 1983, 23(3): 187-223. [29] HOEK E, Martin C D.Fracture initiation and propagation in intact rock——A review[J].Journal of Rock Mechanics and Geotechnical Engineering, 2014, 6: 287-300. [30] 王哲.平面应变状态下混凝土力学行为的三轴试验研究[J].土木工程学报, 2012, 45(10): 62-71. WANG Zhe.Tri-axial experimental study of the mechanical behavior of concrete in plane strain state[J].China Civil Engineering Journal, 2012, 45(10): 62-71. [31] SATAPATHY S, BLESS S.Calculation of penetration resistance of brittle materials using spherical cavity expansion analysis[J].Mechanics of Materials, 1996, 23(4): 323-330. [32] ZHANG M H, SHIM V P W, LU G, et al.Resistance of high-strength concrete to projectile impact[J].Int.J.Impact Eng., 2005, 31: 825-841. [33] FREW D J, FORRESTAL M J, HANCHAK S J.Penetration experiments with limestone targets and ogive-nose steel projectiles.ASME J.Appl.Mech., 2000, 67: 841-845. [34] FOSSUM A F, PFEIFLE T W, MELLEGARD K D, et al.Experimental determination of probability distributions for parameters of a salem limestone cap plasticity model[J].Mechanics of Materials, 1995, 21: 119-137. Penetration model for concrete-rock targets based on hoek-brown criterion CAO Yangyueye, JIANG Zhigang, TAN Qinghua, MENG Chaomei (College of Basic Education, National Universityof Defense Technology, Changsha 410072, China) The cavity expansion theory is a common method to establish an engineering model for penetration problems.Based on a target’s elastic-cracked-comminuted response model, a new semi-infinite spherical cavity expansion model for brittle materials, such as, rock and concrete was built here.The material in the comminuted region was assumed to obey Hoek-Brown yield criterion.The static cavity expansion stress was obtained, and used as an alternative for the penetration resistance in the two-stage penetration model proposed by Forrestal.A predicting model of penetration depth for rigid projectiles penetrating a semi-infinite brittle material target was developed.It was shown that compared with previous models,the proposed prediction model here is more adaptive,especially, for high strength concrete and rock targets. penetration; concrete-rock target; engineering model; cavity expansion; Hoek-Brown criterion 国防科学技术大学优秀研究生创新资助(S150901) 2015-11-11 修改稿收到日期:2016-02-22 曹扬悦也 女,硕士,博士生,1991年3月生 蒋志刚 男,博士,教授,1961年9月生 TV331;TD313;O347.3 A 10.13465/j.cnki.jvs.2017.05.008
2 刚性弹侵彻深度预估公式
3 侵彻试验算例分析

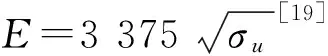
4 结 论