优化情境创设 提高教学效益

【摘 要】当前情境创设中存在情境偏离教学目标，片面理解情境，情境远离学生实际，忽视情境的简洁性与可行性等问题。针对上述问题进行分析并提出改进建议：情境要围绕“问题”和课堂核心目标创设，情境要有“数学味”，要考虑情境的适切性。

【关键词】情境创设；数学问题；数学思维；数学味

【中图分类号】G633.6 【文献标志码】A 【文章编号】1005-6009（2017）19-0039-03

【作者简介】韩新正，江苏省泰州市海陵学校（江苏泰州，225300）校长，高级教师，泰州市学科带头人。

《义务教育数学课程标准（2011年版）》（以下简称《标准》）在第四部分实施建议中指出，要创设合适的问题情境，激发学生的学习兴趣，并在学习中获得“四基”和“四能”。[1]但在实际教学中，关于数学问题情境的创设还存在一些问题。下面，笔者结合案例谈谈自己对创设数学问题情境的一些想法，供大家交流。

一、例析情境创设中的问题

1.情境偏离教学目标，缺少直抵本质的问题导引。

情境本是为激发学生的学习兴趣创设的，是学习新知的先行组织者。如果过分注重情境的生活化和娱乐性而忘记了教学目标，那么教学就会走上弯路，教学目标就难以实现。

【案例1】一位教师讲“直线”这一概念时，设计了如下的教学流程：（1）播放十分钟左右的电视连续剧《西游记》的片段；（2）讨论孙悟空的金箍棒是怎么来的；（3）提问金箍棒有什么特点；（4）说明直线概念。[2]结果学生强烈要求“视频再播放得长一点，还不过瘾”；回答金箍棒是怎么得来的学生讲得兴高采烈，回答金箍棒有何特点却只能说出“要多大有多大，要多长有多长”。整节课学生都沉浸在孙悟空的故事情节中，由于缺少直抵“直线”本质（直的、无限长、向两端延伸）的问题导引，学生无法关联起“金箍棒”和“直线”内在本质的联系。

【分析】情境是为导入新课服务的，所以，情境的创设既要简洁又要不失“数学味”。本案中教师播放了十分钟的电视剧片段，时间长，冲淡了主题，缺乏直抵“直线”本质的追问，从情境到目标之间出现了岔路，学生顺着电视剧的情节在讨论，而没有进行由“金箍棒”抽象出“直线”的思维活动，以致后来的课堂教学无法正常进行。其实，本节课教师可以这样设计：“同学们一定看过《西游记》吧？请你从数学的角度来思考孙悟空的金箍棒吧。（1）金箍棒是笔直的吗？世界上还有比它更直的东西吗？（2）它是一端可以伸长，还是两端都可以伸长的？（3）它的伸长是有限的还是无限的？”然后引导学生得出直线的概念，最后指出直线在现实世界中是不存在的，在我们的数学世界中把类似金箍棒这样的东西理想化为直线。

2.片面理解情境，只考虑“生活现实”。

《标准》在教材编写建议中指出：呈现内容的素材应贴近学生现实。学生的现实主要包括以下三个方面，生活现实、数学现实、其他学科现实。同理，根据数学知识的发生、发展过程来考虑，课堂情境的创设也可以从上述三种现实进行选择。但有不少教师把情境片面理解为“生活现实”，以致逼仄了自己的思维。数学家张奠宙教授提出的“超经验”教学，指的就是为从数学的内部自然生长知识而创设的“数学现实”，它是新知识的起点和生长点，揭示的是数学内部最本质的联系。

【案例2】笔者听的一次评优课，授课内容是“直线和圆的位置关系”，教材提供的素材是太阳从海平面升起的生活现实，于是所有的参赛教师都选择了这一情境，因为大家认为“太阳与地平线的关系”是直线与圆的关系的“真实写照”，没有人想到创设“数学现实”或“其他学科现实”。

【分析】这一情境能让学生感受到数学与生活的关系，但忽视了学生的学习起点，与学生之前已经学过的各种位置关系毫不相关，忽略了知识体系的构建和学习方法的迁移。事实上，学生已经学过比较多的位置关系，比如点和圆的位置关系，两直线的位置关系。本节课可以从复习点和圆的位置关系开始，把点换成直线，自然生长出直线与圆的位置关系，再类比点与圆的位置关系中的半径（r）和圆心与点的距离（d）的大小关系，来研究直线与圆的关系的数量表示。这样的情境建立在学生已有的“数学现实”基础之上，注重了知识的自然生长，关注了知识间内在的逻辑联系。笔者最近观摩了几节李庾南老师的教学录像，李老师就常常使用“数学现实”导入新课，迅速架起了联系新旧知识的桥梁，从旧知识生长出新知识，强化了知识间的逻辑关联，教学自然流畅。

3.情境远离学生实际，无法激发学生兴趣。

我国幅员辽阔，各地差异较大，在一些学生看似平常的“生活现实”，对于另一地区的学生來说就很陌生，甚至难以理解。如果创设的情境学生需要很长时间才能理解，甚至无法理解，课堂教学就很难从“情境”自然过渡到探究、猜想等活动中去，激发学生的学习兴趣更是无从谈起。所以，选择情境必须立足学生的生活实际和认知现状。

【案例3】笔者所在的地区是平原地带，多数学生没有登山的经历。一位教师在讲“一元一次不等式组”第一课时，创设了如下情境：某种杜鹃花适宜生长在平均气温为17～20℃的山区，已知这一地区海拔每上升100米，气温下降0.6℃，现测出山脚下的平均气温是23℃，估计适宜种植这种杜鹃花的山坡的高度。教师用PPT展示出这一情境之后，立即有学生质疑：海拔越高，离太阳越近，气温不是越高吗？怎么反而会下降呢？于是学生展开讨论，教学秩序被打乱。

【分析】本节课创设的情境，目的是为了引入不等式组的概念，但这样的情境确实达不到预期的效果。首先，学生很难理解为什么随着海拔的上升，气温会下降（这是由于缺乏生活经验和地理知识造成的理解障碍）；其次，准确列出气温与海拔高度的关系不是一件容易的事，如果没有教师的指导，很多学生是无法列出这样的不等式的。创设情境的目的旨在导入新课，让学生在非常愉悦的心境下进入新知识的学习和探究，相对于一节课的内容来讲，它是序曲、铺垫。如果学生在情境上花费太多的时间，甚至花了时间都列不出式子，还怎么导入新课？因此，本例可做如下改进：一个钝角的度数为（5x-35）°，请大家列出有关x的不等式（组）。这一情境简洁且有数学味。

4.忽视情境简洁性，教学引入冗长低效。

情境创设应回归简洁性和数学性。情境是导入新课的前奏，是探究新知的铺垫，其性质就决定了情境的简洁性。在实际教学中，部分教师过分追求情境的真实性和过程性，花费了大量的时间用于情境准备而忽视了课堂目标，甚至忘记了教学目标，对课堂缺少整体把握，致使课堂教学本末倒置，课堂核心内容无法完成。

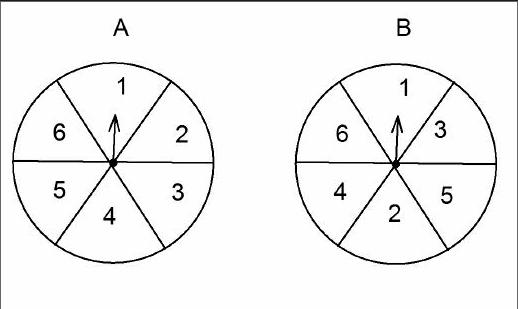
【案例4】一位教师讲“游戏公平吗？”第一课时[3]，设计如下情境：如图，（1）甲自由转动转盘A，乙同时自由转动转盘B；（2）转盘停止后，指针指向几就顺时针走几格，得到一个数字（如在转盘A中，如果指针指向4，就按顺时针方向走4格，得到数字2）；（3）如果得到的数字是偶数就得1分，否则不得分；（4）转动10次转盘，记录每次得分的结果，得分高的为胜者。

第一环节，教师出示两个转盘，口述游戏规则，并用不同的力量转动两个转盘，问学生指针所指的位置，时间约为5分钟；第二环节，将学生两个人分一组，拿出课前准备的转盘，一个人为A盘，另一个人为B盘，让学生自由活动，教师巡视，约9分钟；第三环节，三名学生在讲台上进行展示，两人操作，一人记录，其他学生观看，教师不时进行指导，最后得出结论：甲同学转动转盘A获胜，时间约为8分钟。

整个活动耗时22分钟，且仅仅是创设了情境，没有探讨甲为什么获胜，活动过程无数学味，压缩了探究“游戏公平”本质的时间。

【分析】活动的三个环节松散，耗时过多，可以进行适当整合，第一环节，教师用2分钟时间讲解规则，第二、三环节合并，三名学生在讲台上做，同时，下面三人一组进行合作，最后各组交流，约6分钟，这样情境部分只需8分钟即可。同时在游戏中思考如下问题：两个转盘转动后指针落在每个数字上是随机的吗？是等可能的吗？为什么转盘A总能得到偶数？最后聚焦两个转盘的数字分布。导入新课后直抵“游戏公平”的本质分析。这样课堂就不会出现头重脚轻的现象了。

5.忽视活动可行性，强行得出结论。

通过数学活动创设情境，引导学生通过观察、实验、猜想等活动方式来获得数学结论，并在过程中积累活动经验，培养思维能力，这本是很好的教学手段，但在实际运用中，部分教师不顾活动的可行性，想当然地开展活动，导致活动无法完成，最后只能强行得出结论，草草收场。

【案例5】一位教师在教学“勾股定理”第一课时[4]，创设了如下的情境：请同学们画一个直角三角形，要求两直角边分别是3cm和4cm，并量出斜边是多少？几分钟的画图、测量后有学生举手发言。

学生1：4.9cm。

教师：再量一次。（期望同学们得到预设答案5cm）

学生1：还是4.9cm。

教师：你量得不够准吧，这样吧！取近似值，精确到1cm，结果为多少？

学生2：5cm。（不知道学生2是真量出此结果还是猜到了教师想要的答案）

教师：请同学们再画一个直角三角形，要求两直角边分别是5cm和12cm，并量出斜边是多少？

……

后面的结果可想而知，如果没有教师的暗示，要想量出准确数据还真不容易。

【分析】教师预设是通过学生多次尝试画直角三角形和测量边长，然后根据测量的数据发现直角三角形三边之间的关系，进而发现勾股定理的结论，这样的想法是好的，但实际操作中，画图和测量的每一步都可能出现误差。由于铅笔的粗细不同、视线的影响等，学生很难作出准确的线段长度和直角，测量出现误差在所难免。没有准确数据的保证，观察、猜想就成无源之水了。本案例可做如下改进，用几何画板进行实验，教师在几何画板中画出直角三角形，然后拖动三角形进行大小变化，让学生记下三边的大小，然后分小组合作，探究三边之间的关系。（其他如黄金分割，三角形相似的判定定理的发现都可以用几何画板实验来探究）或者，直接采用教材的情境，利用图形的“割”“补”来发现正方形面积之间的关系，进而发现三边之间的关系。

二、归纳情境创设的三个要点

情境创设本身不是目标，只是一种策略。落实教学目标，突破教学重、难点才是情境创设的根本目的，那种游离于教学目标的情境创设仅仅是一种时髦的形式，只能导致教学活动的费时低效。[5]如何创建激发学生兴趣的、适切的、直抵教学本质的情境呢？我们不妨从数学问题情境的三个核心词开始思考：问题、数学、情境。

1.情境要围绕“问题”和课堂核心目标创设。

情境是吸引学生参与到数学活动中来的一种手段，它不是教学的目的。“问题”是数学的核心，有效的情境起始于有效的问题，这就要求在情境中巧妙设计数学问题，教师要基于问题设计情境，学生要带着问题进入情境，自然进入学习状态，在课堂核心目标的引领下完成教学。例如案例1中，教师虽然创设了《西游记》的情境，但没有让学生带着问题进入情境，所以学生就把情境当成电视剧欣赏起来了。

2.情境创设要有“数学味”。

数学课堂上的所有活动，如创设情境、实验、探究等都是指向“数学”的，没有数学的活动只是游戏，没有数学的探究只是好奇，没有数学味的情境只是形式。只有把课堂的核心目标细化成具有数学味的问题蕴含于情境之中，学生在情境的引领下进入愤悱状态，才能自然进入数学的探究和学习过程中。案例1中，从金箍棒抽象出直线的概念，需要找到金箍棒和直线相通之处，笔者设计的三个问题恰恰揭示了直线的本质，学生带着这些问题进入情境，经过思考、抽象得出直线的概念。案例2中，所有参赛教师创设的都是生活情境，没有创造数学情境，他们忽视了学生的学习起点，忽略了知识体系的构建和学习方法的迁移。如果从复习点与圆的位置关系开始，把点换成直线，自然生长出直线与圆的位置关系，这样的情境建立在学生已有的“数学现实”基础之上，注重了知识的自然生长，关注了知识间内在的逻辑联系，岂不更有数学味？

3.創设情境要考虑“情境”的适切性。

创设情境的本意是为了吸引学生积极参与到教学活动之中，是课堂教学的热身阶段，目的是激发学生兴趣，为新的学习提供先行组织者，在情境的吸引下自然进入探求新知的过程中，这就要求情境“适切”教学目标，符合学生认知规律，便于教学过程顺利进行。情境的选择通常有三种，我们可以选择生活情境，也可以选择数学情境，还可以选择其他学科情境（比如通过物理公式认识反比例函数等）。本文所举的五个案例在“适切”性上均存在一定的问题。案例1忽视了情境的数学性，偏离教学目标，导致整个活动就是看电视剧讨论金箍棒，而无法由金箍棒抽象出直线的概念。案例2忽视了学生的学习起点，忽略了知识体系的构建和学习方法的迁移，忽视了数学现实的创设。案例3忽视了对学生认知基础的了解，学生无法想象山上的气温会随着高度上升而降低。案例4忽视了情境的简洁性，导致活动时间过长，揭示数学本质的时间被压缩。案例5忽视了情境的可操作性，理论上动手操作，发现规律是可行的，但实际中画图、测量的误差无法避免，导致活动难以顺利进行。

情境创设有其教学价值，在数学教学中创设适切的情境，能有效激发学生的学习兴趣，使其自然进入探求新知的过程中。但情境创设中存在的问题也不容忽视，还需要从理论和实践上进行研究和探索。

【参考文献】

[1]义务教育数学课程标准（2011年版）[S].北京：北京师范大学出版社，2012.

[2]袁武.对于求真务实课堂教学的探索[J].中学数学教学参考：下半月，2007（10）.

[3]方卫.活动要善于揭示本质[J].中学数学教学参考：中旬，2009（06）.

[4]钱云祥.基于有效对话的教学策略研究[J].中学数学教学参考：中旬，2014（08）.

[5]钟文琴.创设情境，提高初中数学课堂有效性[J].中学数学：下半月，2010（08）.