春兰秋菊 互有长短——理性选择求二面角余弦值的方法

广东省徐闻县徐闻中学(524100) 钟聘

春兰秋菊 互有长短
——理性选择求二面角余弦值的方法

广东省徐闻县徐闻中学(524100) 钟聘

立体几何中的二面角问题是高考的高频考点,题目一般是中等难度.自从新课标引入了向量知识,使得求二面角余弦值的方法在以往综合法的基础上又多了一个以向量为工具的向量解法.向量法又细分为基向量法及空间向量坐标法.当前学生对综合法听得懂,解题时却无法作出辅助线,功亏一篑;而对坐标法听得清,也喜欢使用,但解题时计算错误,满盘皆输.这也是高三师生一直困惑的问题.笔者受文[1]的启发,通过例题的解法,进行方法的比较,分析每一种解法的适用条件,难易程度,利于以后理性选择求二面角问题的最佳方法.

1 方法比较

方法综合法基向量法空间向量坐标法思路找或用定义法、垂面法作出二面角的平面角,需要添加辅助线.把空间角转化为平面角,求三角形各边并由余弦定理求解.需选择一个适当的基向量,在两个半平面分别作公共棱的垂线或无需添加辅助线.用基向量表示垂直棱的向量或表示两个半平面的法向量,再求向量夹角,然后定号.需建立合适的空间直角坐标系,在两个半平面分别作公共棱的垂线或无需添加辅助线.用坐标表示垂直公共棱的向量或求两个半平面的法向量,再求向量夹角,然后定号.适用条件能找出二面角的平面角或能作出二面角平面角,且均能求出三角形的边.每个基向量的模(长度)可求(已知)且每个基向量的夹角(或关系)已知.能依据几何体的特征建立空间直角坐标系且相关点的坐标能求.

2 例题呈现

图1

(2016年全国高考理科数学乙卷18题)如图1,在以A,B,C,D,F为顶点的五面体中,面ABEF为正方形,AF=2FD,∠AFD=90°,且二面角D−AF−E与二面角C−BE−F都是60°.

(I)证明:平面ABEF⊥平面EFDC;

(II)求二面角E−BC−A的余弦值.

3 例题解析

(I)由已知可得AF⊥DF,AF⊥FE,FE∩FD=F,所以AF⊥平面EFDC.又AF⊂平面ABEF,故平面ABEF⊥平面EFDC.

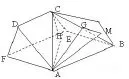
图2

(II)解法1(综合法)如图2,由平面ABEF为正方形知AB//EF,则AB//平面EFDC,所以AB//CD,又二面角D−AF−E与二面角C−BE−F都是60°,且AF⊥平面EFDC,AF//BE,所以∠DFE=

点评二面角的平面角问题,可通过找(作)、证、算、下结论的几个步骤来解决.既可用定义法或垂面法作出二面角的平面角,也可用两个距离即点到公共棱及点到半平面的距离来解决.本解法可理解为垂面法或用两个距离来计算,避开找或作二面角平面角的难点,但求距离是难点且要判断二面角的大小才能定号,是易错点.

图3

解法2(综合法)如图3,过点A作AG⊥BC于G,过G作GH⊥BC交BE于H,连接AH,则∠AGH是二面角E−BC−A的平面角.由解法1知AG=

点评该解法利用定义法作出二面角的平面角,其余弦值不需通过判断二面角大小来定号.显然,在作二面角的平面角辅助线不难,但要解决三角形三边的求值,所以本解法求所作出三角形的三边是重点及难点.

图4

解法3(空间向量坐标法)如图4,过D作DO⊥EF,垂足为O,由(I)知DO⊥平面ABEF.以O为坐标原点,方向为

点评该解法利用向量坐标表示法相关运算来求两个半平面的法向量来解决问题,即是用代数运算代替了几何思维,便于学生掌握,是学生青睐的方法.但寻找一点并判断从该点引出的三条两两相互垂直的直线是重点及难点,还要判断二面角大小定号,是易错点.

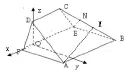
图5

解法4(空间向量坐标法)如图5,建立坐标系同解法3,过点A作AM⊥BC于M,过E作EN⊥BC于N,由

点评该解法利用向量坐标表示法相关运算来求两半平面公共棱的法向量来解决问题,学生容易忽略.两个法向量同时指向公共棱或从公共棱指出时,则两法向量的夹角的余弦值即是二面角的余弦值,减少余弦值的符号错误.

图6

点评该解法利用了基向量法,是学生使用较少的方法,本法选用从一点出法的三个不共面的向量作为基底,通过求出两个半平面的法向量来解决问题,避开了找建系条件的难点,但找一点出发的三个基底的大小及夹角(关系)是重点及难点.

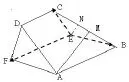
图7

4 反思

从以上解法对比可知,用综合法或向量表示法或基向量法求二面角的余弦值都有破题的重点及难点,所以只要审清题目条件,结合这些方法的适用条件理性选择最佳方法,就可以把问题迎刃而解,提高解题效率.

[1]黎伟初,理性选择“求异面直线所成角”的三种求解方法.[J].中学数学教学参考(高中)2006.9.上半月.