让学生拥有更多的可能性——《认识小数》教学设计与思考

袁晓萍（特级教师）

【教学内容】

北师大版三年级上册第80、81页。

【教学过程】

一、顺势而导，直奔重点难点

学生在认识小数之前，已经对小数有一定的生活经验和知识基础。随着学生生活经验的积累，概念的同化应该成为他们获得小数概念的主要方式。

教学片断1：记录价格，体会小数的价值

师：这里是买一本数学书要花的钱，你能把这本书的价格记录下来吗？

（出现了两种记录价格的方法：6元7角6分和6.76元）

师：两种记录方法，你更喜欢哪一种呢？

生：我喜欢第一种，因为第一种记法容易看懂。

生：我喜欢第二种，因为第二种记录方法方便、简单。

师：两种方法各有长处，而第二种记数方法更简单、明了、方便，今天我们就一起来研究这样的数。

【思考：小数的产生是生产和生活中计量的需要，这个片断的教学，引导学生进一步体会小数产生的价值。】

二、自主交流，分享经验积淀

小数是学生生活中非常熟悉的“数”，“颜值”不高，“内涵”不够，因此在新课学习时往往会遭遇“内外”兼失、乏善可陈的尴尬境地。教师在教学中应注重丰富多元的自主学习，让学生充分发挥个体经验基础，使自主学习最大化。

教学片断2：头脑风暴，自主交流小数的基本知识

师：小数怎么读？怎么写？哪里有？表示什么？同学们能自学关于小数的知识吗？你可以用“我知道……”“我想问……”这两句话，也可以用这些小数作材料，把你知道的关于小数的知识在小组内交流一下！

生：我知道超市的标价牌上有小数，我们测量的时候也要用到小数。

生：我知道计算的时候也可能产生小数。

生：我知道写小数的时候，小数点一定要写成小圆点，不要写成顿号。

生：我会读小数，65.65元读作六十五点六五元。

师：哪一部分和我们以前的读法不一样？

生：小数点我们就读作“点”，小数点左边就按照整数的读法读数，右边要按顺序一个数字一个数字地读。

生：我知道65.65元应该付65元6角5分。

师：0.09元和0.90元这两个以元为单位的数里面都是两个“0”，一个“9”，为什么表示的价格却不一样呢？

生：9所在的位置不一样，所表示的钱数就不一样。

师：这些表示商品价格的小数，同学们是怎么理解的？

生：小数点左边的数表示几元，小数点右边第一个数表示几角，第二个数表示几分。

【思考：对于小数，学生在生活中有着丰富的生活经验，教师以“我知道……”“我想问……”为向导，引导学生展开数学探究和发现之旅，让学生在自然、放松的课堂环境中自主交流，学生的学习情绪就会高涨。就在这种看似平淡、随意的交流中，教师引导学生带着“怎么读、怎么写、哪里有、表示什么”这几个问题进行交流，巧妙地激活和引导着学生的思维。】

自主的课堂，让教师的角色发生了巨大的变化，教师更多的责任是引发学生提出问题、引导学生理解问题、引领学生运用知识。课堂转变成师生之间、生生之间自由轻松的互动、交流、分享、答疑、解惑的场所。

教学片断3：自主质疑，探底学习小数的疑难困惑

师：关于小数，你还有哪些想知道的问题？

生：我想问，小数点后面能不能是三个数字？

生：我想问，整数部分的元可不可能是几百元？

生：我想问，有没有最大的小数？

生：我知道，没有最大只有更大，因为数是可以无限大的。

生：我想问，小数的历史和小数是谁发明的。

师：通过“我知道”的交流和“我想问”的相互启发，同学们自主学习了这么多关于小数的知识。我们一起来看一段与小数有关的视频，看看能不能知道更多关于小数的知识。

（播放微课：小数的历史）

【思考：提出问题不仅是数学研究的重要组成部分，也是数学教学的重要目标。教学中通过引导学生回忆所学的知识，以类比思维引导学生提出一个个“小数领域”中更有研究价值的问题。通过提问，让意犹未尽的学生带着问题看微课，了解更多小数的历史与发展。】

三、沟通联系，完善数系结构

教师在教学时基于学生已有认知结构，从整数计数方法的知识结构出发，把小数看作整数计数的概念推广，以十进制表示数（量）为基础，学生的“数概念”学习就会轻松许多。

教学片断4：感受小数的十进关系

（出示：1元、1角、1分三枚硬币）

师：这3个“1”表示的意思一样吗？1.11元再加0.04元是多少？再加0.40元是多少？

师：你能再接着往后数吗？

（学生用实物数数）

生：1.56 元、1.57 元、1.58元、1.59元……然后满了 10分，就要向前一位进一。

师：好一个“满十进一”，我们跟着一起往后数吧！

生：1.60 元、1.70 元、1.80元、1.90元，满十进一，2.00元。

师：刚才我们一起数钱的过程，你熟悉吗？让你想起了什么？

生：我们以前数整数的时候，也是这样数的。

小结：我们以前学的整数知识在学习小数的时候也能用上，它们的计数方法差不多。

【思考：通过圈钱、数钱的环节，让学生在小数学习时不仅满足于会认、会读、会写小数，还要回答一些更为本源的问题，比如小数和自然数是什么关系？尽量把构建“小数”背后的数学思想方法用学生易懂的方式表示出来，用学生已经熟悉的十进制位值系统的知识结构来同化小数的概念，对学生来说，更容易理解小数的意义，因为这对其知识结构的构建来说，不仅能凸显小数的本质，也是十进制位值系统完善的需要。】

四、引导迁移，丰盈活动体验

学生只有在参与中体验、感悟数学，才能真正领略数学的魅力。教师在教学中可以采用语言表征、实物表征、分数表征、画图表征等多维表征方式，让学生逐步建构小数的本质内涵，并上升为以符号表征为主的形式化理解，以此帮助学生建立良好的数感。引导学生在活动体验的基础上感悟，在感悟中提升认识，使学生对数的理解上升到更高的水平，使学生对“小数”的理解从感性认识上升到理性认识。

教学片断5：多元表征，感受小数与分数的联系

1.提出任务：怎样在计数器里表示0.8？除了计数器，还能用其他方法表示0.8吗？

（课件出示）

提出学习建议：以四人小组为单位，用画一画、标一标、圈一圈、写一写……这些方法，尽可能用不同的方法表示出0.8。

反馈学生的作品：

教师引导学生寻找联系：你觉得哪些表示方法是相似的？哪些表示方法稍稍改变一下，就和其他作品相似了？

生：①和②相似的，把①放进②就一样了。

生：把①中每个硬币用珠子线段表征，就可表示⑥了。

生：①、②、③、④都差不多，都表示了10份里面取8份。

生：④和⑤也差不多，就是窄一点，细一点。

【思考：从另一个角度讲，分数的意义也是小数意义的基础。学生在这一主题活动中的学习体验，首先利用图形的各种表征，加深对小数的理解，丰富小数的内涵；其次利用图形直观，渗透分数与小数的联系。在寻找各种表征方式的过程中，彻底拓展学生的思维，让学生在头脑中构建小数的图形表征的各种可能，学生在寻找联系的过程中，加深对小数的理解，渗透数系扩展的思想，使学生能更完整地认识小数的本质。】

2.小结：让我们一起来整理一下同学们的表示方法。

（课件演示：由钱币图到长方形图，由线段的表示过程到计数器，再到数位顺序表的变化过程）

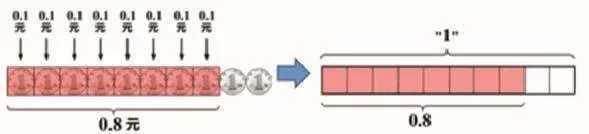
生：“0.8”可以用多种方式来表达。

生：这些表达方式之间都是有联系的。

生：0.8就是10个当中的8个。

【思考：此时的微课有效发挥了“微提示，深思考”的价值作用，整个过程用时不多，却自然充分、一气呵成，引导学生积极进行观察、分析、比较、概括、表达。学生通过微课将原本个体细碎的思考链接成整体，有方法、有思考、有情趣，知识与技能自然达成，促进了认知与元认知彼此交融，拓展了思维的宽度和深度。】

【课后反思】

一、整体构建，注重概念系的建立

将概念放到关系网中，在概念的相互联系中去认识概念，是一种比较有效的教学方法。小数是生活中不能用自然数计量时产生的新数，它与自然数都是用来计量的，遵循十进制位值系统的一切规则。张奠宙教授指出：小数是十进制计数沿着另一个方向（越来越小）的延伸，不是分数的附庸。整数的计数方法已存在于学生的认知结构中，本节课不是孤立地认识小数，而是充分利用学生的数概念基础，将小数放在数的体系中，让学生创造小数的计数方法，使其原有认知与新的概念形成一个全新的认知系统，从而深刻理解小数的意义，从数（整数、小数）的整体关系网中，感受到数之间的联系与区别，从而更系统地认识小数。

二、数形结合，在变化中感受不变

《认识小数》属概念教学，较为抽象、凝炼。根据学生对概念的认知，一般遵循：感知——表象——抽象概括——形成概念这一规律。本课中，教师充分挖掘和利用概念中的直观成分，采用数形结合的方法，利用直观模型，帮助学生认识小数，了解以“元”为单位的小数的含义，体会小数和整数的相似性，普通的钱币、长方形、线段图及数轴组合在一起，所要传达的却是促进学生学习的重要策略——数形结合的思想，把数与形在同一时空中呈现，将小数具体化、形象化，并让学生在相互比较与联系中感受，在不同中看到相同，在变化中看到不变，其目的是让学生对小数含义的理解变得多维而深刻。

三、学法迁移，关注经验的生长省悟

学生建构数学概念的过程，绝不能是一个教师简单告诉的过程，学生的概念学习需要经历一种经验性的活动过程。具体地，在小数含义建构过程中，教师应该引导学生通过操作体验，主动沟通小数与整数的联系，理解小数的含义。经历不等于经验。投入数学实践性活动，要能够脱身出来，对经历的学习过程进行反思省悟。同时，教师要承认学生不同的认知起点，作为组织者将学生课堂生成的材料有选择的通过展示沟通、对比交流、分析总结，学生对小数含义的理解才是主动的、生动的。