行“通融”之径进“无痕”之境

许贻亮

“无痕，是教育的至高境界。”怎样的教育是无痕教育？笔者基于无痕教育的理念，在教学实践中提出并践行了“通融数学”——行“通融”之径，进“无痕”之境。

“通融”是两个词语的叠加，其一为“通”，其二为“融”。通，心理学上类似于“顺应”，在“顺应中求通”，从而明白到“原来是这样啊！”“通”含有：通俗、通道、直通、通透、变通等之义。融，心理学上类似于“同化”，在“同化中求融”，从而感悟到“它们是一样的！”“融”含有：融合、融洽、融和、融化、融通等之义。其根源在于无痕教育，追求的是在教学中“有情有理，有法有度”，让一切教学资源“自然和谐”，从而达成不露痕迹、重剑无锋、润物无声的无痕境界。

中医上说，“通则不痛，痛则不通”，想通了、理通了，学习就水到渠成了。如教学物体的运动方式“旋转”时，“顺时针”怎样让学生通透地理解？如果我们反复地强调“像时针、分针那样旋转的方向就是顺时针”，这样便要求学生理解并掌握“顺时针”就显得有点无理了。如果教师能够用简单、通俗的数学语言，简洁易懂地说清其数学本质，通透的理解就可达成。譬如，借用钟面上的12个数字，其中12既是终点又是起点，还可以看作0，从而就形成了一个有序的等差数列：0、1、2、3、4、5、6……如是观之，当旋转时经过的区域对应的数字是从小到大的，即为顺时针，反之即为逆时针。这样就“通”了，无需死记硬背，学生自然可感悟到“原来是这样啊！”这样教学，进入了潜移默化中理解的“无痕”之境。

与此同时，教者应有广阔的教学视野，生活与数学、现代与古代、数学与其他学科、知识的前世今生未来等无一不是教学的优质资源。如果能纵观全局，聚零为整，融多为一，那么产生的价值将大大超过“1+1＝2”。如教学《比例的认识》时，可以问学生：“比例，我们今天刚学，它是全新的知识还是以往就学过的旧知识？”帮助学生梳理知识之间的联系，可以感知到其和商不变规律、分数的基本性质、比的基本性质等“形变质不变”。

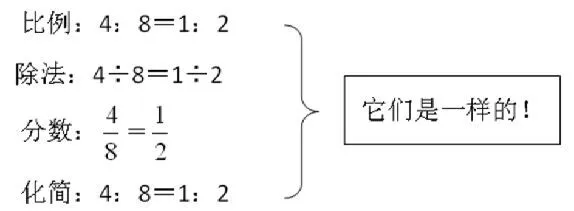
这样，学生在不知不觉中思考、分析、对比，便无缝地融入原有的认知结构中，体会到数学之间丰富的联系，感悟到“变中不变”的数学思想，达成春风化雨中提升数学能力的“无痕”效果。

“有之以为利，无之以为用。”“通融”与“无痕”是“目与纲”的关系，纲举目张；“通融”与“无痕”是“枝与根”的关系，根深枝茂；“通融”与“无痕”是“形与神”的关系，神足形备。下面，以北师大版五年级上册《分数的再认识》一课为例，展开来谈。

一、通融之间应不露痕迹

让学习在“不知不觉中开展”是无痕教育的实践策略之一。如何做到？通俗与融合可以做到。通俗，就是低起点，能够让学生无声中感到亲切。融合，就是巧蕴蓄，能够让学生不露痕迹地思考、深入。

教学中，在先简单地回顾三年级学过的分数内容：把谁平均分？平均分几份？取了多少份？怎么读？怎么写？怎么算？接着，逐次出示如下教学素材：

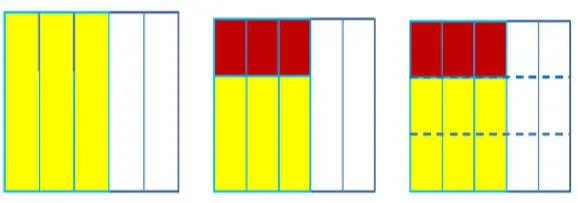
第1图，属于旧知的范畴；第2图，就属于新知的领域，这时涂色的部分占了整个长方形的几分之几？是八分之三、十一分之三、十五分之三？学生在观察与思考中展开“变通”之旅：画辅助线，一条不够，再画一条，如第3图。这里，素材是通俗的：长方形；问题是通俗的：阴影部分占几分之几？但在这通俗之中，先“分”再“数”，“分数，先分一分，再数一数”的理解与感悟却在不知不觉中展开，既浅显易懂又深刻到位。这样教学，比纠结于“一个整体”有几种情况？“若干份”是什么意思？等更有教学的价值。

二、通融之间应重剑无锋

让学习“在循序渐进中掌握”是无痕教育的实践策略之一。如何做到？通透与融化可以做到。通透，就是看得清，能够让学生破除认知中的迷障；融化，就是化得了，能够把新知融入原有认知结构之中。

如本教学单元中，有着关于“大于1的分数”的认识，这是教学的难点。其难在于，学生在三年级学习分数的初步认识之后，其思维中关于分数也就有了个不完善的“前概念”，以为“等于1的分数”已经是最大的分数了，因此“大于1的分数”难以理喻。在教学中，我以数轴为载体，让学生思考：“往下数是几？”

教学中，退到学生的已有旧知和思维起点，从一份数起，再一份一份地累加。道生一、一生二、二生三、三生万物。从已经是最大的”认知冰点到“分数也可以无限大”的思维热点，再把分数的数、整数的数、小数的数融在一起，感悟其中的“同”：它们是一样的！认知就这样在对话中无声无息地达成。

三、通融之间应润物无声

让学习“春风化雨中提升”是无痕教育的实践策略之一。如何做到？变通与融通可以做到。变通，就是会活学，能够让学生具体问题具体分析；融通，就是会活用，能够让学生彼此相连，融会贯通。

如教学“两个未知的整体，比较取相同分率或不同分率的部分，无法确定”。我们提供怎样的教学素材合适些？——谁取的乒乓球多？

方案一：

方案二：

如果采取方案一，学生常滞于物，囿于两个两箱可见的大小关系，常问的问题是“第一个箱子里面可以放几个第二个箱子？”难以跳出具象的思维全方位地考量三种不同情况。而采取方案二，则学生常能顿悟出：“都有可能！”甚至会“小大人”的口吻道：“不知道，别乱说！”从比较两个已知整体到比较两个未知整体，从确定性思维到不确定性思维，挑战的是学生的分析、想象、推理等数学素养。教学中，改变的只是把第二个小箱子换成一个集合图，便能够帮助学生跳出认知的误区，教学中，学生多数人第一反应都是“第二个箱子取出的乒乓球多大于在有人质疑的情况下，变通之旅随之展开，通过举例知道也有可能第二个箱子取出来的多。这时，可以引导思考：“怎么两种想法都对呢？”明白本题的独特性“未知的两个整体”，让学生经由“同化”“顺应”再到认知“平衡”。不自见，故明；不自是，故彰。教学中，一问一疑一导，教师似乎只是在穿针引线，没有做鲜明的强调或教学，而学习于此就润物无声地达成了。“处无为之事，行不言之教。”折射出来的是“真水无香”的无痕追求。

无痕教育，言有尽而意无穷。在实践中、在思考中、在研究中，越是前行，对于前方的风景就越是期待。