《两位数乘两位数》教学尝试与反思

覃佳韵

【教学内容】

浙教版三年级上册第60、61页。

【教学过程】

一、情境引入

师：我们学校的同学准备去看球赛，你能从图中找到什么数学信息？

生：我在图中找到关于足球票价格的信息——甲级票的价格是28元/张，乙级票的价格是23元/张。

生：我在图上看到的信息是，15位同学买甲级票，19位同学买乙级票。

师：你们能通过这些数学信息提一个数学问题吗？

生：15位同学买甲级票一共花了多少钱？

生：19位同学买乙级票，他们买票花了多少钱？比买甲级票的钱多还是少？

二、研究28×15的计算方法

师：我们先来解决买15张甲级票，一共需要多少钱？

生：15×28，28×15。

师：这两个算式是一样的，那老师就这样写：28×15。

师：算式列出来了，答案等于多少呢？这就是我们这节课要研究的《两位数乘两位数》的计算。

【设计意图：从生活情境引入，引导学生经历整理信息、提出问题的过程，培养图文阅读能力。进而从情境中抽象出算式，产生计算两位数乘法的需要，转入相关的数学学习。】

师：28×15你们会算吗？别着急，今天我们不只是要比谁算得对，还要比一比谁想到的方法多？谁的方法好？

（学生尝试——教师巡视，选择部分学生答案誊抄）

（学生集体反馈）

师：请停笔。老师找了一些方法比较有特点的同学，我们把这些方法编上号，请他们先来介绍自己的方法。

生 ：28×15= （20+8）×15=20×15+8×15=420①我先把28拆成20和8，再乘以15，也就是20×15+8×15=420。

师：听懂他的方法了吗？他是把哪个数拆分开了？

生：把28拆成20+8的和。

生：28×15=28×（10+5）=10×28+5×28=420②我先把15分成10和5，再乘以28，也就是 10×28+5×28=420。

师：同学们，你们看懂他是怎么拆的了吗？

生：把15拆成10+5的和。

生：这两种方法都是把其中一个因数拆成一个整十数加一个一位数的和。

生：接下来都可以应用乘法分配律计算整十数乘两位数和一位数乘两位数。

生：28×15=（30-2）×15=30×15-2×15=450-30=420③把28分成30-2，先算 30×15-2×15，再算 450-30，等于 420。

生：他是拆成了两个数的差。

生：28×15=28×5×3=140×3=420④我先把15拆成3×5，先算 5×28 等于 140，再算3×140等于120。

生：他是把15拆成3×5的积，没有用乘法分配律，用的是乘法结合律。

师：真有眼光！这里还有一位同学是这样的算法，比较特别，请你也来介绍介绍吧！

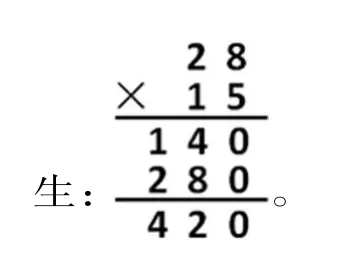
⑤我先算五八四十，写0进4，再算二五一十，与进上来的40加起来，就是140。再算一二得二，就是200，2写在百位，一八得八，8个十，写在十位，这样加起来是420。

师：这些方法的答案都是420，看一看，想一想，你们能给这些方法分分类吗？

生：第①、②、③种分成一类，他们都是用乘法分配律来计算的。第④种分成一类，它利用的是结合律。第⑤种再分一类，别的都是横式，它是竖式。

师：其他同学的想法呢？

生：我建议把第⑤种竖式也分到第一类。你们看，竖式的第一层算的就是28×5，第二层算的是28×10，相当于把15分成了10+5的和，用的其实也是乘法分配律。

小结：28×15的算法有很多，既可以利用乘法分配律进行计算，也可以利用乘法结合律。同样利用乘法分配律，有的同学用横式计算，有的同学用竖式计算。

【设计意图：充分考虑学生已有的认知基础，鼓励学生自主探索、构建新的算法，感悟化归的思想方法。通过交流，丰富学生个体的认知，增加思维的发散性。在理解各种算法步骤及其依据的基础上，进行分类，突出基本的算理——乘法分配律和乘法结合律，培养思维的深刻性。】

三、研究23×19的计算方法

师：刚才我们解决了第一个问题，后面还有一个问题“买19张乙级票，一共需要多少钱？”怎样列式？

生：23×19。

师：这也是两位数乘两位数，你们也能把它算出来吗？现在请你们动笔写一写。

（学生尝试——教师巡视，选择部分学生答案誊抄）

师：我看到很多同学已经算出来啦，而且不止一种方法。现在我们看这位同学是怎么算出来的。

生：23×19=23×（10+9）=10×23+9×23=230+207=437。

生：23×19=（20+3）×19=20×19+3×19=380+57=437。

师：计算根据的是什么？

生：乘法分配律！

师：还有其他方法吗？

生：我用 23×（20-1）。

师：这位同学把19看成了？

生：20-1。

师：他的算法是分配律还是结合律呢？

生：分配律。

师：还是分配律。那老师就有疑问了，为什么你们都是用分配律，没有用结合律呢？

生：因为23和19都不能拆成几和几相乘。

师：但是23和19可以拆成一个整十数和另一个数相加或相减。

师：所以这道题我们不能用乘法结合律，只能用乘法分配律。看来，计算两位数乘两位数时，乘法分配律的应用范围会比较广一些。

【设计意图：通过设计数据，巧妙地让学生体会到乘法分配律的通用性和乘法结合律的适用性。从探索“多法”到深入“通法”经历的是一个理性选择的过程，这样的过程，有助于学生体会数学学科的特点，培养学生的自主精神和理性精神。】

四、研究竖式算理，与乘法分配律建立联系

师：这道题也有同学用竖式计算。两位数乘两位数的竖式我们还没有正式学习过，让我们重点来研究一下——

师：他是怎么算的？“207”是从哪里来的？

生：207是23×9得到207。（教师在竖式旁对应板书：23×9）

师：下一层的“23”呢？

生：是23×10得到的。（教师对应板书：23×10）

生：为什么竖式只写了23？

生：“23”中的3是和十位对齐的，说明是23个十，就是230。

生：十位上的“1”乘“23”得到23个十，直接在十位处写23就可以了。

小结：直接相乘，算起来比较快；写在对应位置上，就可以表示相应的数值。

师：老师也进行了计算，请你们看看我是怎么算的？算得对吗？

（如果学生有高位算法就展示学生的）

高位算式:

生：老师只是把230和207位置换了一下。

生：老师算23乘10。

师：能不能请同学完整地介绍一下老师的算法？我第一步是算什么？第二步是算什么？我的方法和你们的方法有什么不同？

生：老师的这种竖式是先算23乘10，从高位开始算，我们的竖式是先算23乘9，从低位开始算。都是利用乘法分配律，结果是一样的。

师（指板书）：28×15也有同学写了一个竖式：

你们看看这个竖式属于——

生：属于28×10＋28×5，高位算起。

师：你还能够根据乘法分配律，作出不同的拆分、写出不同的竖式吗？

生：我把28拆成20和8，先算15×20得300，再算15乘8得120，最后加起来得420。

师：这是高位算起还是低位算起？

生：高位。

生：我还能写一个低位算起的竖式。

小结：同样根据乘法分配律，拆分方法不同，计算顺序不同，可能写出不同的竖式。

【设计意图：竖式也可以多样化。提供多样的竖式，允许学生选择自己喜欢的算法进行计算，在使用和比较的过程中，一是进一步感悟基本算理——乘法分配律。二是体会算法的自主和自觉，自主是指：哪些是算法可以变化的部分，哪些是不能变化的；自觉是指：不同算法有什么优点？适合计算什么样的数据？等等。】

【教学反思】

浙教版《两位数乘两位数》的编写与一般教材不同。从课程的脉络上看，浙教版先安排学习乘法分配律和乘法结合律，帮助学生准备好了知识基础，使算法的探究成为可能。从课时编排看，浙教版不只强调竖式算法，还为学生预留了自主的空间，通过设计因数的特点来调控教学的进程。例题 1“28×15”，学生既可以根据乘法分配律计算，也可以利用乘法结合律来计算；例题2“23×19”，聚焦到乘法分配律，进而聚焦到竖式计算。在这样的过程中，学生始终在主动地思考、选择和创造。

理解到浙教版教材的这些意图，并通过与张天孝老师及其团队面对面的交流，我对《两位数乘两位数》一课的认识从“计算”提升到了“能力”。原来，教一节计算课，不仅是要让学生会算，更要通过学会算的过程，发展思维的深刻性、灵活性和创造性。因此，在课堂上，我对这样的理念进行了充分的实践和小小的创造。

首先，根据三年级学生的特点，创设看球赛的情境，激发学生的兴趣，引起计算的需要；其次，充分信任学生的潜能，直接把“28×15”的计算任务抛给学生，鼓励学生根据自己的认知储备和认知偏好，自主探索各种算法。通过交流，来丰富和深化个体的认识，包括：1.听取和理解不同的算法；2.分类，理解不同的算法背后相同的依据。尤其是突破“横式”和“竖式”的表征，认识到竖式的计算原理；3.体会一道题有不同的算法，培养思维的开放性。再次，利用素数“23×19”，引导学生感悟乘法分配律的通用性，并正式学习新算法——竖式算法，结合算理的理解突破竖式写法上的一些特殊性。最后，对经典竖式再作突破，引导学生根据乘法分配律及竖式的书写约定，创造新竖式，包括高位算起和低位算起、包括第二因数去乘第一因数和第一因数去乘第二因数等等，帮助学生再次体会到算理的主导性和算法的创造性。

诚如学生在陈述课堂收获时所说的，上完这节课，他们不是简单地学会了“两位数乘两位数”的竖式计算，而是把“两位数乘两位数”计算当作一个研究任务，经历了分析和综合的过程、理解和推理的过程、创造和评价的过程，激发和激励了他们的自主性和成就感，锻炼和提升了他们的数学思维能力。