谈如何开发《探索勾股定理》的拓展性课程

姜纪华+毛作洪

摘要：本文以开发《探索勾股定理》的拓展性课程为例，展示了以学校教研组为团队如何依托数学课本开发拓展性课程。以期抛砖引玉。

关键词：数学教学；《探索勾股定理》；拓展性课程

中图分类号：G633.6 文献标识码：A 文章编号：1992-7711（2017）02-0087

众所周知，勾股定理的内容非常丰富，但现行的教材（以浙教版为例）只安排两个课时，教学受课时的限制，不能充分利用勾股定理发展学生的问题解决、人文积淀、理性思维等核心素养。本文以开发《探索勾股定理》的拓展性课程为例，展示以学校教研组为团队如何依托数学课本开发拓展性课程，以期抛砖引玉。中国学生发展六大核心素养中有十八个基本要点，其中三个是问题解决、人文积淀、理性思维，《数学课程标准》的前言中也有类似的表述。对应三个基本要点确定三个课时的拓展性课程，在上完基础性课程的两个课时后进行。因篇幅所限，只展示每个课时的教学目标、学习内容及要求、课外作业。

第一课时：勾股定理在生活中的应用

设置缘由：数学课最缺的是实践课，学生非常喜欢实践课，开发团队成员一致同意每学期开发一节实践课。

教学目标：引导学生观察生活，体验生活中的数学，体验用数学模型刻画现实世界。

活动内容及要求：（1）带学生参观有人字梁结构的农村老宅，请当地手艺比较好的手艺人，一个木匠，一个泥水匠当讲解员。（2）泥水匠展示方地基的方法。造房子时要先奠基，在一百多平方米的地上要设置很多个直角，选好位置打下木桩，固定好线，沿线做墙脚。怎样使墙角正好是直角呢？先沿房子的朝向打下两个木桩，两个木桩之间的距离为三尺，调整第三个木桩的位置，使它与前两个木桩的距离分别为四尺与五尺。拉上线，再微调。泥水匠师傅说，这种方地基的方法是师傅们口耳相传的好方法，若是正式造房子开工方地基的日子，仪式很隆重。（3）木匠师傅主要举了两个例子。一个例子是如何预算建造斜屋顶结构的房子用到的木料，特别是人字梁结构中斜线部分的木料长度的计算方法。第二个例子是如何在大块的板材中确定直角。（4）教师作为主持人、主持师傅与学生的互动，让学生尝试用数学模型解释实际应用问题。

课外作业：找一个生活中实际用到勾股定理的例子，写心得体会交流。

第二课时：勾股定理的历史文化

收集方法：这部分内容多而杂。动员团队所有成员参与，从网上和书本中搜集并整理。

教学目标：在对勾股定理历史了解的过程中，感受数学文化，感受历代世界人民的智慧和探索精神，感受数学知识源远流长和数学价值的伟大。

学习内容及要求：

（1）勾股定理的发现：公元前1100多年的《周髀算经》中，就有勾股定理的记载，相传是商代商高发现的。三国时的赵爽给出了证明，2002年北京国际数学大会的徽标就是赵爽证明勾股定理用的弦图。勾股定理被西方人称为毕达哥拉斯定理，是古希腊数学家毕达哥拉斯于公元前550年发现的。相传毕达哥拉斯花了很多的精力才证明了这个定理，他很高兴，于是宰了百头牛庆贺一番，不过毕达哥拉斯对勾股定理的证明方法已经失传。这个定理有流传很广，印度、希腊、巴比伦、中国、埃及等文明古国对此定理都有所研究。要求学生课前和课后整理出赵爽和毕达哥拉斯的相关成果，了解《周髀算经》等中国古代经典数学著作。

（2）勾股定理巨大辐射能力：①勾股定理是数与形结合的典范，启发后人对函数的研究；②毕达哥拉斯学派的希帕索斯利用勾股定理导发现了根号2，引发了第一次数学危机，数从有理数扩展到实数；③勾股定理使数学在追求逻辑体系和数学美的过程中发展了现代数学；④勾股定理中的公式是一个最早的不定方程，引发了包括著名的费马大定理。⑤勾股树的拓展，勾股树中的正方形可以变换为正三角形、半圆、月亮形等许多图形。要求学生例举数形结合的例子；能描述三次数学危机；能举例一些现代数学；了解费马大定理的内容及费马的成就。

（3）勾股定理的证明方法多样化。由于勾股定理的证明起点很低，所以千百年来下至业余数学爱好者、普通的老百姓，上至著名的数学家、国家总统都参与了勾股定理的证明。勾股定理有四百多种证明方法，目前还找不到一个定理的证明方法之多能超过勾股定理。

“总统”证法的故事：1876年一天的傍晚，美国的议员伽菲尔德由于受到了两个小孩的追问，开始对勾股定理证明进行思考……后来他在继承的基础上反复思考终于找到了独特的证法。1876年，伽菲尔德在《新英格兰教育日志》上发表了他的证法。由于在1881年伽菲尔德就任美国第二十任总统，人们就把这一证法称为“总统”证法。要求学生课前和课后搜集有趣的勾股定理证明故事并交流。

第三课时：勾股定理的证明方法

证明方法选择的标准：证法有四百多种，但不能穷尽，要选择重要的、典型的、适合初中学生的证法。

教学目标：在勾股定理的探索过程中培养学生的理性思维和创新能力，体会深层次的数形结合；发展形象思维，体验解决问题方法的多样性，培养探索精神。

学习内容及要求：

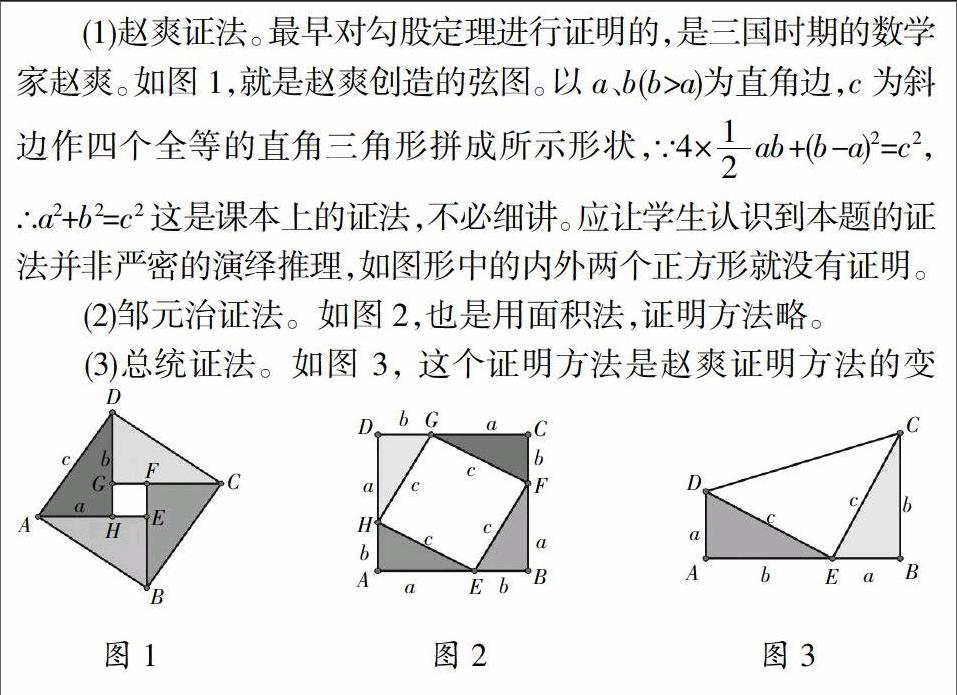
（1）赵爽证法。最早对勾股定理进行证明的，是三国时期的数学家赵爽。如图1，就是赵爽创造的弦图。以a、b（b>a）为直角边，c为斜边作四个全等的直角三角形拼成所示形状，∵4×（1/2）ab+（b-a）2=c2，∴a2+b2=c2这是课本上的证法，不必细讲。应让学生认识到本题的证法并非严密的演绎推理，如图形中的内外两个正方形就没有证明。

（2）邹元治证法。如图2，也是用面积法，证明方法略。

（3）总统证法。如图 3， 这个证明方法是赵爽证明方法的变形，也是用面积法，证明方法略。

（4）欧几里德证法。如图4，以a、b、c分别为直角边斜边Rt△ABC，再分别以a、b、c为边，在直角三角形外部作正方形ABED、CBKG、ACHF，连结BF、CD，过C作CL⊥DE，交AB于点M，交DE于点L.∵AF=AC，∠FAB=∠CAD，AB=AD，∴△FAB≌△CAD.∵S△FAB=（1/2）a2，而S△CAD等=（1/2）S矩形ADLM，∴S矩形ADLM=a2。同理可证，S矩形MLEB=b2.∵S正方形ADEB=S矩形ADLM+S矩形MLEB，∴c2=a2+b2，即a2+b2=c2。应让学生认识到本题的证法是典型演绎推理，是欧氏几何，后面两种证法也是如此。

（5）相似三角形性质证法。如图5，Rt△ABC中，a、b、c分别为直角边斜边，过点C作CD ⊥AB，垂足为D.可证得△CAD∽△BAC， ∴AD/AC=AC/AB，∴AC2=AD× AB.同理BC2=BD× AB，∴AC2 +BC2=AB（AD+ BD）= AB2，即a2+b2=c2。

（6）切割線定理证法。如图6，Rt△ABC中，a、b、c分别为直角边斜边，以B为圆心、a为半径作圆，交AB及AB的延长线分别于D、E，则BD=BE=BC=a，因为∠BCA=90°，点C在⊙B上，所以AC是⊙B的切线。由切割线定理得AC2=AD×AE=（AB-BD）（AB+ BE） =（c-a）（c+a）=c2-a2， 即b2=c2-a2，所以a2+b2=c2。

（7）证法评析。中国证法的独到之处是善用面积法，巧妙地避开了角的性质及平行线性质的繁琐理论，简洁明了，吴文俊、张景中等发展的数学机械化方法深受中国古代数学思想的影响。后三个证法追求严谨的逻辑体系，对提升人们的理性精神，注重演绎推理的科学精神具有不可替代的地位。

课外作业：找一种勾股定理的证明方法与学生交流。

总之，要设计好《探索勾股定理》的拓展性课程，开发团队要有广阔的数学视野、深厚的数学史功底以及良好的数学理解能力。