单相全桥谐振直流环节软开关逆变器

王强， 单瑞香， 王天施， 刘晓琴

(辽宁石油化工大学 信息与控制工程学院，辽宁 抚顺 113001)

单相全桥谐振直流环节软开关逆变器

王强， 单瑞香， 王天施， 刘晓琴

(辽宁石油化工大学 信息与控制工程学院，辽宁 抚顺 113001)

为提高逆变器的效率和简化控制方式，提出一种单相全桥谐振直流环节软开关逆变器。通过单独开关控制辅助谐振电路，使直流环节电压在逆变器主开关需切换时下降到零，逆变器的主开关可以实现零电压开关，同时辅助开关也可以实现零电压开关。而且，逆变器直流环节电压不会超过直流源电压。由于谐振过程和零电压持续时间都较短，因而可以减少功率消耗和提高直流电压的利用率。依据不同工作模式下的等效电路，分析其工作原理，结合相平面分析法研究其动力学行为，给出了软开关实现条件和参数设计过程，搭建了实验样机。实验结果表明逆变器的主开关和辅助开关都实现了软开关，可以有效地降低该软开关逆变器的开关损耗和提高其效率。

谐振；逆变器；软开关；单独开关；零电压

0 引 言

随着当今社会电力电子技术的快速发展，在直流变换器领域里软开关技术取得了显著的成就，使人们对在逆变器方面使用软开关技术产生了浓厚的兴趣。传统硬开关会涉及如低的开关频率、对环境的电磁干扰、高开关损耗和音频噪声等问题[1]，因而软开关技术就会显得尤为重要。在20世纪80年代末，谐振直流环节软开关逆变器由美国的Divan博士首次提出，由于其具有结构简单、控制方式简便的优点，该方面领域的专家给予了很大重视，是目前软开关逆变器的主要发展方向。但是传统的谐振直流环节软开关逆变器在很多方面还面临着不少问题，如电压应力大，谐振电压的峰值过高，电压过零点的时刻难以与逆变器开关时刻同步[2]。

文献[3]提出的谐振直流环节逆变器虽然辅助电路里只使用了1个辅助开关，但辅助电路的无源器件除了1个谐振电感外，还有两个相互耦合的谐振电感，辅助电路结构相对复杂，较难控制，且其谐振电压峰值高于直流源电压。文献[4-7]提出的软开关逆变器虽然其直流环节电压峰值没超过直流源电压，但其辅助电路设置了3个辅助开关，控制相对繁琐。文献[8-10]提出的箝位谐振直流环节逆变器的电压虽然被嵌位在直流源电压的1.3倍附近，但是需额外设置箝位开关、箝位电容等辅助元件才可以实现其功能，会增加硬件成本。

本文提出了一种新型单相全桥谐振直流环节软开关逆变器，对上述的缺点和不足进行了改进，且具有以下特点：1)辅助谐振电路只有1个辅助开关器件，控制相对简单，且直流环节电压没有超过输入直流电源电压，主开关和辅助开关都可以实现零电压开关；2)辅助谐振电路的谐振元件只使用了1个谐振电感和1个谐振电容，且谐振电容的端电压可近似认为恒定，电路结构与控制都相对简单；3)谐振过程时间较短，消耗的功率较小，且直流环节零电压持续时间短，直流电压的利用率得以提高。本文通过一个开关周期内不同工作模式的等效电路图，对每个模式的工作方式做了详尽的分析，给出了软开关实现条件和参数设计过程，并建立起了辅助谐振电路损耗的数学模型，最后用实验去验证上述的新型拓扑电路的有效性。

1 电路结构和基本工作原理

1.1 电路结构

图1为单相全桥谐振直流环节软开关逆变器配置图，由直流电源Edc、辅助谐振电路，桥式逆变器和阻感性负载构成。直流环节开关Sdc、缓冲电容Cdc、反并联二极管Ddc、谐振电感Lr和谐振电容Cr共同构成了辅助谐振电路，桥式逆变器由开关S1-S4，反并联二极管D1-D4和缓冲电容Ca组成。桥式逆变桥应遵循如下原则：(a)正向功率转移：当输出为正半周期时，S1-S2工作，续流由S2-D4(或S1-D3)完成。当输出为负半周期时，S3-S4工作，续流由S4-D2(或S3-D1)完成；(b)反向功率转移：当V0为正时， D1-D2参与功率转移，续流由S4-D2完成；当V0为负时，D3-D4参与功率转移，续流由S2-D4完成。为简化分析做以下假设：1)各个元件的运行可以认为在理想条件下；2)谐振电感与负载电感相比很小，因而逆变桥开关状态过渡瞬间的负载电流可以等效为恒流源I0；3)用Si、Sa等效逆变器的主开关器件，用Di、Da等效与其反并联的二极管。具体等效原则：(a)正向功率转移：当输出在正半周期时，开关Si等效于S1，开关Sa等效于S4且一直保持关断(在负半周期到来时，负载电流I0将流过S4)；当输出在负半周期时，开关Si等效于S3，开关Sa等效于S2且一直保持关断(在正半周期到来时，负载电流I0将流过S2)。(b)反向功率转移：当V0为正时，开关Si等效于S1(在V0的负半周期到来时，负载电流I0将流过D3)，开关Sa等效于S4；当V0为负时，开关Si等效于S3(在V0的正半周期到来时，负载电流I0将流过D1)，开关Sa等效于S2；4)电容Cs为Cdc和桥式逆变器的缓冲电容Ca的等效电容，其大小为Cs=Cdc+2Ca；5)由于谐振电容Cr足够大，因而通过它的电压近似恒定为Ea，且远小于直流源Edc，可以设Edc=(10-20)Ea。图1所示的拓扑结构可等效为图2所示的电路，各部分的电流和电压的正方向如图1、2所示。

1.2 基本工作原理

正向功率转移以输出在正半周期为例，对其工作原理进行分析，在一个开关周期内本电路分为7个工作模式，电路的特征工作波形与工作模式的等效电路分别如图3、图4所示，由于等效开关Sa一直关断，因而工作模式分析中，Sa可以忽略。

图1 谐振直流环节逆变器主电路Fig.1 Main circuit of resonant DC-link inverter

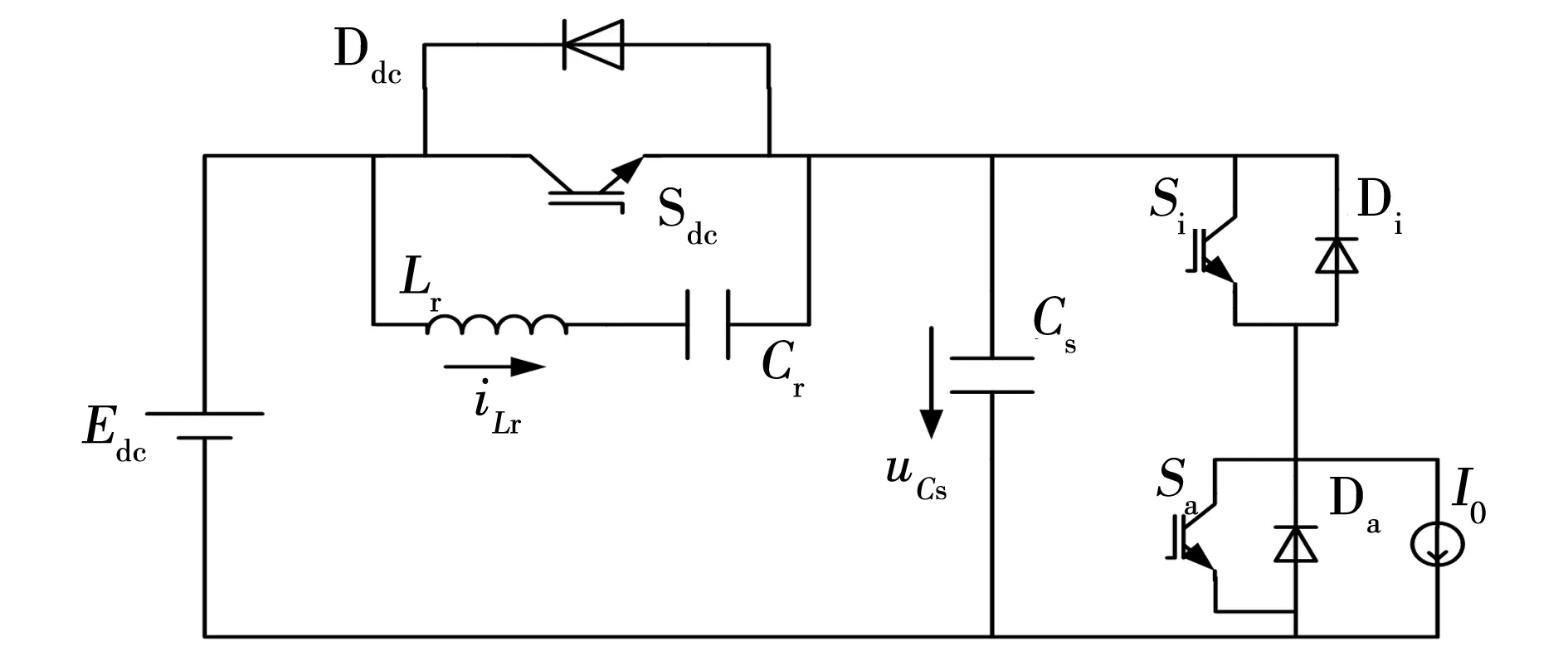
图2 谐振直流环节逆变器的等效电路Fig.2 Equivalent circuit of resonant DC-link inverter

图3 电路的特征工作波形Fig.3 Characteristic waveforms of circuit

图4 各工作模式的等效电路Fig.4 Equivalent circuits under different operation modes

模式1(t0～t1)：在t0时刻，iLr(t0)=-Ia，uCs(t0)=Edc，负载电流I0从二极管Da续流，电感Lr与电容Cs谐振，Cs放电，Lr被充电，uCs逐渐减小，iLr逐渐增大，在t1时刻，当uCs衰减至零时，模式1结束。本模式运动轨迹如图5(a)中t0-t1段，本模式运动曲线方程为

(1)

将uCs(t1)=0代入式(1)中，可以得到Lr的电流值Ib1为

(2)

本模式中uCs(t)，iLr(t)的表达式分别为

Eacos[ωr(t-t0)]。

(3)

iLr(t)= -Iacos[ωr(t-t0)]-

ωrCsEasin[ωr(t-t0)]。

(4)

Sdc关断瞬间的电压变化率为

(5)

本模式持续时间为

(6)

模式2(t1～t2)：在t1时刻，二极管Di导通，电感Lr的电流经Di反向线性减小，同时流经Da的电流线性减小，在t2时刻，当iLr为零时，流经Di的电流为零，因而其自然截止，模式2结束。本模式持续时间为

(7)

模式3(t2～t3)：在t2时刻，Si开通，由于开通前直流环节电压为零，因而实现了零电压开通，iLr线性增加，流经Da的电流线性减小，当iLr增至I0时，通过Da的电流为零，然后二极管Da的反向恢复电流开始流动，在t3时刻，当Da截止时，模式3结束。

trr是二极管Da的反向恢复时间，则反向恢复电流Irr的表达式为

(8)

本模式持续时间为

(9)

模式4(t3～t4)：在t3时刻，负载电流经开关Si流动，电感Lr与电容Cs谐振，Lr和Cs都被充电，iLr和uCs逐渐增大，在t4时刻，uCs增加为Edc时，iLr达到最大值Ip1，模式4结束。本模式的运动轨迹如图5(a)中t3～t4段。本模式的运动曲线方程为

(10)

将uCs(t4)=Edc代入式(10)中，得Lr最大电流值Ip1为

(11)

本模式中uCs(t)，iLr(t)的表达式分别为

uCs(t)= (Edc-Ea){1-cos[ωr(t-t3)]}+

Irrωrsin[ωr(t-t3)]。

(12)

iLr(t)=I0+Irrcos[ωr(t-t3)]+

(13)

本模式持续时间为

(14)

模式5(t4～t5)：在t4时刻，二极管Ddc导通。iLr流经Ddc线性减小，在t5时刻，流过Lr的电流衰减为I0时，Ddc自然截止，模式5结束。本模式持续时间

(15)

模式6(t5～t6)：在t5时刻，Sdc开通，因为Sdc开通前两端电压为零，所以完成了零电压开通。iLr经开关Si线性减小为零，此时流经Sdc的电流增至I0，然后iLr开始经Sdc反向增加，iSdc也持续增加，在t6时刻，当通过电感Lr的电流达到设定值-Ib2时，开关Si断开，由于并联缓冲电容的存在，开关Si实现了软关断，模式6结束。本模式持续时间为

(16)

模式7(t6～t7)：在t6时刻，Da导通，负载电流I0从Da续流，iLr反向线性增加，在t7时刻，当iLr为-Ia时，开关Sdc关断，电容Cs降低了Sdc的电压上升率，Sdc实现了零电压关断，模式7结束。本模式持续时间为

(17)

然后电路从模式1继续工作，开始下一个开关周期。至此，一个开关周期的电路曲线运动方程建立完成，可以绘制出相平面上的运动轨迹，如图5(a)所示。

图5 谐振直流环节逆变器的相平面Fig.5 Phase-plane of resonant DC link inverter

反向功率转移以V0为正为例，来分析电路的工作原理，一个开关周期内可以分为8个工作模式，图6、图7分别为电路的特征工作波形与工作模式的等效电路。

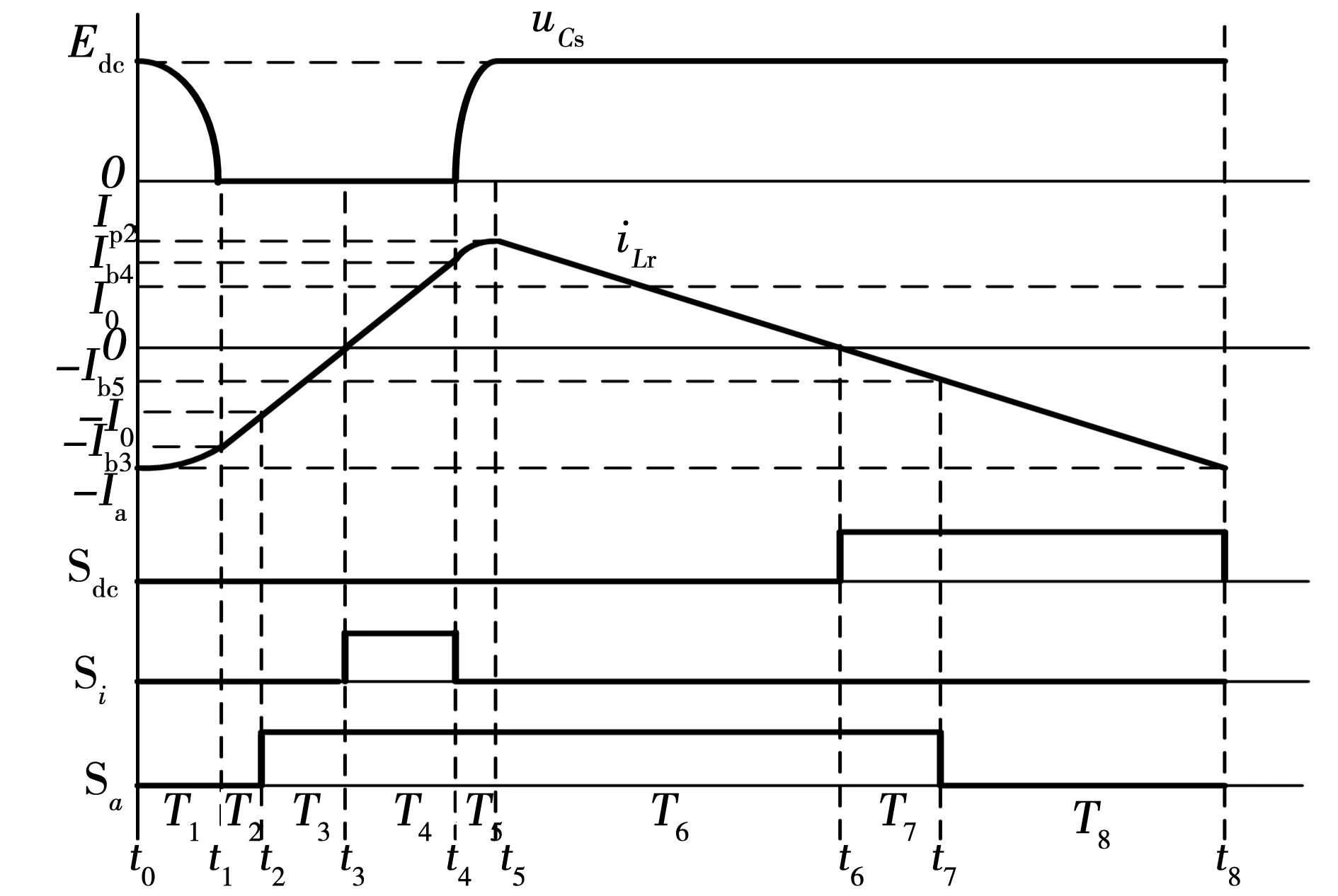
图6 电路的特征工作波形Fig.6 Characteristic waveforms of circuit

图7 各工作模式的等效电路Fig.7 Equivalent circuits under different operation modes

模式1(t0～t1)：在t0时刻，iLr(t0)=-Ia，uCs(t0)=Edc，负载电流I0经Di流向直流环节，电感Lr与电容Cs谐振，电容Cs放电，电感Lr被充电，uCs逐渐减小，iLr逐渐增大，在t1时刻，当uCs衰减至零时，模式1结束。本模式运动轨迹如图5(b)中t0-t1段，本模式运动曲线方程为

(18)

将uCs(t1)=0代入到式(18)中，可以得到Lr的电流值Ib3为

(19)

本模式中uCs(t)，iLr(t)的表达式分别为

Eacos[ωr(t-t0)]。

(20)

iLr(t)= -(Ia-I0)cos[ωr(t-t0)]-

ωrCsEasin[ωr(t-t0)]-I0。

(21)

本模式持续时间为

(22)

模式2(t1～t2)：在t1时刻，二极管Da导通。电感Lr的电流经Da反向线性减少，在t2时刻，当iLr为-I0时，二极管Da截止，模式2结束。本模式持续时间为

(23)

模式3(t2～t3)：在t2时刻，Sa开通，由于开通前直流环节电压为零，Sa实现了零电压开通。负载电流I0经Sa续流，Lr的电流反向线性减少，在t3时刻，当iLr为零时，二级管Di截止，模式3结束。本模式持续时间为

(24)

模式4(t3～t4)：在t3时刻，开关Si开通，由于开通前，直流环节电压为零，Si实现了零电压开通，iLr经Si，Sa线性增加，在t4时刻，当iLr为Ib4时，模式4结束。本模式持续时间为

(25)

模式5(t4～t5)：在t4时刻，Si关断，在Cs的作用下，Si的端电压不能突变，因而实现了零电压关断，电感Lr与电容Cs谐振，Lr和Cs都被充电，iLr和uCs逐渐增大，在t5时刻，当uCs增加为Edc时，iLr达到最大值Ip2时，模式5结束。本模式的运动轨迹如图5(b)中t4～t5段。该模式的运动曲线方程为

(26)

将uCs(t5)=Edc代入到式(26)中，得到Lr的最大电流值Ip2为

(27)

本模式中uCs(t)，iLr(t)的表达式分别为

(28)

iLr(t)=Ib4cos[ωr(t-t4)]+ωrCs(Edc-Ea)sin[ωr(t-t4)]。

(29)

本模式持续时间为

(30)

模式6(t5～t6)：在t5时刻，二极管Ddc导通。iLr经Ddc线性减小，在t6时刻，当iLr减为零时，Ddc自然截止，模式6结束。本模式持续时间为

(31)

模式7(t6～t7)：在t6时刻，Sdc开通，因为Sdc开通前两端电压为零，所以Sdc完成了零电压开通。iLr经Sdc反向线性增大，在t7时刻，当iLr为-Ib5时，模式7结束。本模式持续时间为

(32)

模式8(t7～t8)：在t7时刻，开关Sa关断，由于缓冲电容的存在，因而实现了软关断。二级管Di开始导通，负载电流I0经Di流向直流环节，iLr反向线性增加，在t8时刻，当iLr为-Ia时，开关Sdc断开，且电容Cs降低了Sdc的电压上升率，Sdc实现了零电压关断。模式8结束。本模式持续时间为

(33)

然后电路从模式1继续工作，开始下一个开关周期。至此，一个开关周期内的电路的曲线运动方程建立完成，可以绘制出相平面上的运动轨迹，如图5(b)所示。

1.3 软开关实现条件及设计规则

以下分析以正向功率转移为例，反向功率转移的分析方式与其相似，因此不再分析。

1)为确保Sdc实现零电压关断，器件允许的电压变化率应大于等于其开通瞬间的电压变化率，即

(34)

2)为确保Sdc实现零电压开通和逆变器正常向负载供电，Sdc应在t4-t5时间段内开通，Sdc处于开通状态的时间TSdc(on)应满足

T6+T7≤TSdc(on)≤T5+T6+T7。

(35)

3)为使逆变桥上的主开关Si实现零电压开关，直流环节的电压必须减为零，由于Edc远大于Ea，因而Ea可以忽略，由式(3)可得

(36)

4)为了限制反并联二极管Da因反向恢复电流引发的损耗，因而其反向恢复电流的变化率应不大于设定值A。即

(37)

5)谐振电容Cr与谐振电感Lr的谐振频率fr与开关频率fc相比应该很小，谐振频率fr为

(38)

6)为确保逆变器桥臂上的主开关可以实现零电压开通，同时便于控制，在实际应用中软开关逆变器的主开关的切换时刻与硬开关逆变器相比要滞后时间Td，以确保逆变器主开关在直流母线电压下降为零时开始切换，为实现这一目的，需要满足T1≤Td，即

(39)

7)流过谐振电感Lr的最大电流过大会对辅助电路的损耗产生影响，因而其应不大于两倍负载电流最大值I0max。由式(11)可以得到

(40)

8)由于谐振过程中会产生功率损耗，因而逆变器直流环节电压上升和下降的时间不宜过长，因而要设定时间Tv，使T1≤Tv和T4≤Tv，以减少损耗。由式(6)和式(14)得

(41)

(42)

9)逆变器对直流电压的利用率会随着直流环节零电压持续时间的增长而减小，因而每个开关周期的零电压持续时间Tz不宜过长，零电压持续时间与开关周期T之比小于等于设定值B，即

Tz=T2+T3≤BT。

(43)

为在全负荷范围内可以实现软开关，并尽可能减少损耗，当负载电流取最大值时，Lr、Cs、Cr、Ia的取值应满足式(34)至式(43)。

2 辅助电路功率损耗的理论分析

逆变桥上的主开关为零电压开关，开关损耗为零；Sdc实现了零电压开关，开关损耗为零；但是Sdc反并联二极管Ddc存在通态损耗。在理想状态下，Lr、Cs和Cr的功耗可以近似为零，原因是其电阻值很小。辅助开关Sdc与二极管Ddc通态压降可分别设为VCE和VEC，开关频率为fc。

Sdc及Ddc的通态功耗PSdc和PDdc可表示如下：

(44)

(45)

辅助谐振电路的总功耗Padd可表示如下：

Padd=PSdc+PDdc。

(46)

将Irr和Xr1的表达式代入式(45)，根据式(46)，辅助谐振电路的总功耗Padd可表示如下：

(47)

接下来用Padd分别对Lr，Cs，Ib2，Ia求偏导，来研究Lr，Cs，Ib2和Ia的变化对功率损耗的影响。

(48)

由式(48)和式(49)可知其偏导都大于零，因而辅助谐振电路的功率损耗会随着Cs和Lr增大而增大，所以在满足软开关实现条件和设计规则的前提上，Lr和Cs尽量取较小值。

(50)

(51)

由式(50)和式(51)可知其偏导都大于零，因而辅助谐振电路的功率损耗会随着Ia和Ib2增大而增大，所以在满足软开关实现条件和设计规则的前提上，Ia和Ib2尽量取较小值。

3 参数设计过程

参照软开关实现条件及功率损耗分析，参数的设计过程如下。

已知实际电路参数和性能指标：单相全桥软开关逆变器样机额定输出功率P0=4 kW，负载电阻R0=12 Ω，负载电感L0=1 mH，最大输出电流I0max=25 A，逆变器的直流电源电压Edc=400 V，输出电压V0=220 V，缓冲电容Ca=Cdc=20 nF，开关器件允许的关断瞬间电压变化率(du/dt)r=300 V/μs，二极管Da的反向恢复时间trr=120 ns，每个开关周期的直流母线电压上升和下降的规定时间Tv≤5 μs，反向恢复电流的变化率设定值A≤7 A/μs，每个开关周期内直流母线零电压持续时间Tz与开关周期T的比值B≤0.2。开关频率fc=10 kHz。

设计过程：谐振电容满足Cs=Cdc+2Ca=60 nF，由于Edc=(10-20)Ea，可取Ea=(1/13)Edc，即Ea=30 V。

根据式(37)，为限制反并联二极管Da因反向恢复电流引发的损耗，需满足

(52)

考虑到Lr对辅助谐振电路损耗的影响，理论上应取Lr=53 μH，但是为留有一定的裕量，实际上取Lr=60 μH。

根据式(34)和式(36),为确保Sdc实现零电压关断和主开关Si可以实现零电压开关，需要满足

(53)

(54)

可以得到初始电流值Ia的范围，即12.6 A≤Ia≤18 A，考虑到Ia对辅助谐振电路损耗的影响，因而取较小值13 A。

由于谐振电容Cr与谐振电感Lr的谐振频率fr与开关频率fc相比应该很小，可以认为谐振频率fr为3 kHz，由式(38)得

(55)

由于trr=120 ns，由式(8)得到反向恢复电流Irr为

(56)

将上述数据代入式(40)，可以得到通过谐振电感Lr的最大电流值为

(57)

所以参数设计的Ip1满足谐振电流最大值的要求。

(58)

因此，当Td=2.26 μs时，可以确保逆变器的主开关可以在直流母线电压下降到零时完成切换，保证了零电压开通的实现。

由式(41)、(42)和(43)可以得到

T1=2.26 μs≤Tv。

(59)

T4=3 μs≤Tv。

(60)

(61)

通过式(59)、式(60)得出逆变器直流环节电压可以在规定时间Tv内完成上升和下降，由式(61)可以得出直流母线零电压持续时间Tz满足设计要求。

为确保Sdc实现零电压开通和逆变器正常向负载供电，根据式(35)可得辅助开关Sdc开通时间的范围为

(62)

即62 μs≤Ton(Sdc)≤85 μs，因而Ton(Sdc)可以取为70 μs，则辅助开关Sdc的占空比为

ρSdc=Ton(Sdc)fc=0.7。

(63)

根据直流电源电压和谐振电流最大值，可以确定电路中开关器件承受电压不超过400V，承受的电流不超过35A，据此来选择开关器件。

至此，参数设计完毕，以上实际电路参数的设计完全依据软开关实现条件设计规则和功率损耗分析，可以保证电路在全负荷范围内都实现软开关。

4 实验结果

为证明该软开关逆变器的有效性，根据图1搭建了一台实验样机，实验参数选取如下：直流电源电压Edc=400 V，负载电阻R0=12 Ω，负载电感L0=1 mH，逆变器最大输出电流I0max=25 A，输出功率P0=4 kW，谐振电感Lr=60 μH，缓冲电容Ca=Cdc=20 nF，输出频率f0=50 Hz，开关频率fc=10 kHz，主开关切换滞后时间Td=2.26 μs，辅助开关Sdc的占空比为0.7。

图8(a)描述的实验波形为谐振电感电流iLr和谐振电容电压uCs的波形，可以看出uCs存在零电压凹槽，与图3的特征工作波形基本吻合。图8(b)的实验波形为Sdc电压uSdc和Sdc电流iSdc在辅助开关Sdc开通和关断时的变化情况，由于Sdc开通前，其端电压已先降为零，继而iSdc开始上升，Sdc完成零电压开通，Sdc关断时，Sdc的电压以较低的变化率增大,Sdc可以实现零电压关断。图8(c)描述的波形为逆变器的主开关S1的开关状态发生切换时其端电压和电流变化情况，观察图8(c)可以发现在S1开通和关断过程中iS1和uS1的波形没有重叠区，开关损耗可以明显减小，比硬开关逆变器占有优势。图8(d)描述的波形为当输出频率为50 Hz时，单相全桥逆变器输出电流i0的波形变化情况，可以看出逆变器输出电流的波形较平滑，无明显畸变。

图8 实验波形Fig.8 Experimental waveforms

所设计的单相全桥软开关逆变器在效率方面存在优势，为验证其优势所在，在基本相同的前提下和硬开关逆变器进行效率对比实验，二者的输出电压基本保持恒定为220 V，通过使用合适阻值的负载电阻，使二者的输出功率都可以达到4 kW，然后对硬开关逆变器和软开关逆变器的输入功率进行测量，最后得到二者的效率，即输出功率与输入功率的比值。考虑到读取时由于各种原因可能存在误差，所以要采取多次测量取平均值的方式以尽可能的减小误差。在输出功率为4 kW时，软开关逆变器的实测效率达到96.8%，比硬开关逆变器的效率增加了2.3%。在相同条件下，也对本文提出的软开关逆变器和文献[7]提出的谐振直流环节软开关逆变器进行了效率对比测试，测试方式如上，本文提出的软开关逆变器在输出功率4 kW时的实测效率与文献[7]提出的谐振直流环节软开关逆变器相比，效率提高了1.2%，这是因为本文提出的逆变器的直流环节电压与文献[7]相比更低，而且本文电路的零电压持续时间与谐振时间很短，在其它时间，电压基本保持平稳，有效降低了直流环节的损耗和提高了直流电压的利用率，效率会更高；而文献[7]提出的谐振直流环节逆变器在主开关不需要切换时，直流环节电压也会发生大幅度波动，对效率的提高会产生进一步的影响。

5 结 论

本文设计了一种新型单相全桥谐振直流环节软开关逆变器，和其他文献提出的同类型逆变器相比具有以下优点：辅助谐振电路只含有1个辅助开关器件，控制相对简单，且直流环节电压没有超过输入直流电源电压。通过实验得出如下结论：

1)逆变器的开关器件可以在直流母线电压下降到零时开通，实现零电压开通；

2)在谐振电路工作过程中，逆变器的辅助开关实现了零电压开通与关断，且承受的最大电压值没超过直流电源电压；

3)逆变器输出电流的控制效果较好，电流波形基本无畸变；

4)实测效率在输出功率达到4 kW时可达到96.8%，和硬开关逆变器，相似类型的软开关逆变器相比效率更高。

[1] 潘三博,潘俊民.一种新型的零电压谐振极型逆变器[J].中国电机工程学报,2006,26(24): 55-59.

PAN Sanbo,PAN Junmin.A novel zero-voltage switching resonant pole inverter[J].Proceedings of the CSEE,2006,26(24): 55-59.

[2] Bellar M D,WU T S,Tchamdjou A,et a1.A review of soft-switched DC-AC converters[J].IEEE Transactions on Industry Applications,1998,34(4): 847-860．

[3] Jamal Jafar Jafar,B G Fernandes.A new quasi-resonant DC-link interver using single switch for soft switching[J].IEEE Transactions on Industry Applications,2002,17(6): 1010-1016．

[4] PAN Zhiyang,LUO Fanglin.Transformer based resonant DC link inverter for brushless DC motor drive system[J].IEEE Transactions on Power Electronics,2005,20(4): 939-947.

[5] 王军,徐龙祥.软开关技术在磁悬浮轴承功率放大器中的应用[J].电工技术学报,2009,24(6): 85-90.

WANG Jun,XU Longxiang.Application of power amplifier for active magnetic bearing using softswitching technology[J].Transactions of China Electrotechnical Society,2009,24(6): 85-90.

[6] 贺虎成,刘卫国,李榕,等.电机驱动用新型谐振直流环节电压源逆变器[J].中国电机工程学报,2008,28(12): 60-65.

HE Hucheng,LIU Weiguo,LI Rong,et al.A novel resonant DC link voltage source inverter for motor drives[J].Proceedings of the CSEE,2008,28(12): 60-65.

[7] 明正峰,倪光正,周文云,等.直流母线零电压过渡软开关逆变器中点电压不平衡问题研究[J].电工技术学报,2004,19(5): 81-86．

MING Zhengfeng,NI Guangzheng,ZHOU Wenyun,et al.Study of neutral-point voltage unbalancing problem in DC-rail ZVT inverter[J].Transactions of China Electrotechnical Society,2004,19(5): 81-86.

[8] 应建平,沈红,张德华,等.双滞环控制的三相双幅有源箝位谐振直流环节逆变器[J].中国电机工程学报,2004,24(2): 8-12.

YING Jianping,SHEN Hong,ZHANG Dehua,et a1.Two-hysteresis control of three-phase two-amplitude actively clamped resonant DC-link inverter[J].Proceedings of the CSEE,2004,24(2): 8-12.

[9] 祁晓蕾,阮新波．一种新的双幅控制有源箝位谐振直流环节逆变器[J].中国电机工程学报,2008,28(27)：42-47．

QI Xiaolei,RUAN Xinbo.A novel two-amplitude active-clamped resonant DC link inverter[J].Proceedings of the CSEE,2008,28(27):42-47.

[10] 张德华，汪范彬，刘腾，等．一种新型的串联有源箝位谐振直流环节逆变器双幅控制策略[J]．中国电机工程学报，2002，22(7): 7-12.

ZHANG Dehua,WANG Fanbin,LIU Teng,et a1.A novel two-amplitude control strategy for series actively clamped resonant DC-link inverter[J].Proceedings of the CSEE,2002,22(7): 7-12.

(编辑：张 楠)

Single-phase full-bridge resonant DC-link soft-switching inverter

WANG Qiang， SHAN Rui-xiang， WANG Tian-shi， LIU Xiao-qin

(College of Information and Control Engineering,Liaoning Shihua University,Fushun 113001,China)

A single-phase full-bridge resonant DC-link soft-switching inverter was proposed to improve the efficiency and simplify the control method.When main switches in the inverter needed operating,the DC-link voltage decreased to zero via the single switch which controlling the resonance of the auxiliary circuit.Then all main switching devices in the inverter were operated under zero-voltage condition and auxiliary switching device was also operated under zero-voltage condition.The voltage across the DC-link inverter devices was limited to the input source voltage.Because the process of the resonant and the zero-voltage time was short,it could reduce the power loss and improve the efficiency by using the DC-source voltage.The operation principle was analyzed based on the equivalent circuits at different operation modes.The phase-plane analysis technique was established in order to study transient dynamics.The conditions of soft-switching and the process of parameter design were also achieved.A laboratory prototype was built.The experimental results demonstrate that soft-switching operation of all switching devices are realized.Therefore,the soft-switching inverter presented effectively reduces switching loss and improves efficiency.

resonant; inverter; soft-switching; single switch; zero voltage

2015-07-12

国家自然科学基金(51207069); 辽宁石油化工大学国家级科研项目培育基金(2016016)

王 强(1981—),男,博士,副教授,研究方向为软开关逆变器的电路拓扑及控制; 单瑞香(1990—),女,硕士研究生,研究方向为软开关逆变器的电路拓扑及控制; 王天施(1970—),男,博士,副教授,研究方向为电力系统继电保护; 刘晓琴(1975—),女,博士研究生,副教授,研究方向为电力系统故障诊断。

王 强

10.15938/j.emc.2017.03.006

TM 464

A

1007-449X(2017)03-0038-10