非连续供电模式下感应电机低频振荡机理分析

乔鸣忠， 曾海燕， 朱鹏

(海军工程大学 电气工程学院，湖北 武汉 430033)

非连续供电模式下感应电机低频振荡机理分析

乔鸣忠， 曾海燕， 朱鹏

(海军工程大学 电气工程学院，湖北 武汉 430033)

采用对称分量法，排除变频器一侧电感和电容影响，对感应电机在最简单的不连续供电模式下(晶闸管供电)的振荡现象进行研究。通过分析电机在三相及两相导通模式下的换相瞬态过程，考虑转速改变时电机方程各量的变化，推导电机在不同过渡过程时其定转子电流的空间向量表达式，并给出其时域形式解，找到感应电机在不连续供电时产生振荡的原因，从电机本体方面对振荡现象进行解释。应用上述分析方法对一台三相感应电机进行计算，计算结果与实验吻合较好。分析方法可作为进一步研究变频器供电的感应电机的过渡过程的基础。

感应电动机；振荡；不连续供电；过渡过程

0 引 言

感应电机的低频振荡问题一直以来都备受人们关注，对于运行在低转速下的大功率推进用感应电机，这一问题的影响尤为突出。

上世纪60年代，T.A.Lipo和P.C.Krause等人利用小扰动模型对交-直-交-感应电机驱动系统进行分析，得到了系统运行的不稳定域，研究了直流滤波环节以及电机本身参数变化对系统稳定性的影响[1]。之后，Mutoh和Ueda等人对产生低频振荡的因素给出了定性分析，认为电机本身参数匹配性及死区时间影响了PWM 逆变器供电系统的稳定性[4]。文献[6]通过分析低频振荡现象提出采用改变定子频率来抑制低频振荡的方法，取得了一定效果。文献[7]从电力电子非线性现象的角度，通过分岔及混沌理论对系统的不稳定性进行了一些研究。国内对于变频驱动感应电机系统稳定性研究较少。文献[8]通过对低频振荡的仿真和实验现象分析，提出了一种低频振荡判据。文献[9]认为振荡的原因来自于直流环节滤波器与电机之间的自激。文献[10]应用分叉理论对感应电机数学模型进行分析，并未得到不稳定边值条件和不稳定域。文献[11]应用小扰动模型，对不同参数变化时系统的稳定域边界和稳定裕度变化情况进行了详细地分析，得出了各参数对系统稳定性的影响规律。

以上方法大都应用小信号模型作为分析基础。虽然小信号模型能够评价系统的局部稳定性，但不适用于描述非线性系统。另外，上述文献都将变频器引入所分析的系统，并未详细分析电机本体的瞬态过程，所以无法得知振荡产生的根本原因，也不能给出物理解释。文献[12]从断电-重合闸的角度研究了感应电机的过渡过程，其所考虑的情况为三相同时断电及合闸，与感应电机调速系统的实际运行情况不同，而且文中关于定、转子瞬态时间常数的假设与实际相差较大；文献[13]从电机过渡过程的角度分析了同步电机产生振荡的原因和机理，方法值得借鉴，但对于异步电机，由于存在转差率，又增加了计算复杂性。

本文从最简单的感应电机供电模式(晶闸管供电)入手，排除一般变频器直流环节滤波器电感电容参数的影响，从电机本体出发，详细推导了感应电机在不同工作状态切换时的瞬态方程，研究了感应电机的过渡过程，得到了电机在不连续供电模式下的定转子电流和电磁转矩的表达式，全面、准确地描述了低频振荡现象，从根本上找到了感应电机低频振荡的原因。

1 晶闸管供电感应电机数学模型

之所以从晶闸管入手研究是因为其与感应电机构成的调速系统也有低频振荡现象[14]，并且此系统与PWM供电时相比，瞬态过程更简单，排除了电感和电容的影响，非线性环节只有晶闸管，更容易从电机本体来研究振荡问题。

晶闸管-感应电机调速系统如图1所示。

图1 晶闸管-感应电机调速系统Fig.1 Thyristor-induction motor system

感应电机调速系统的接线方式很多，以定子绕组星型接法为例，对上图所描述情况进行研究。为便于分析，做出如下假设：

1)电源为理想电源，输出波形为三相对称正弦波；

2)6个开关管具有相同的特性，对称触发，关断状态时呈阻抗为无穷大，导通状态时其阻抗为零；

3)感应电机为理想电机，其定转子绕组在空间产生正弦分布的磁动势；

4)不计电机磁路饱和以及集肤效应的影响。

1.1 电机的几种工作状态

在列写电机方程时，有必要对系统的工作状态加以说明，因为牵涉到瞬态方程的约束条件和起始值问题。对于星接三相感应电机，运行状态有以下三种：

1)一相导通或三相都不导通。由于星接，此时电机中没有电流；

2)两相同时导通或一相导通，由于星接，一相导通时电机内没有电流流过；

3)三相或两相同时导通。

感应电机一般运行在第三种情况下，即三相或两相同时导通。所以接下来的电机过渡过程分析分为两种情况：三相对称运行和两相不对称运行。此时电机在一个周期内可分为12个过渡过程，每个过程占用π/6，设触发角为α，KZ1～KZ6依次导通。电机的换相顺序如下：

A—B—C→B—C→AB—C→AB—→AB—C—→AC—→ABC—→BC—→A—BC—→A—B→A—BC→A—C→A—B—C。

由于电机具有两相不对称的运行状态，采用对称分量法来建立电机的定转子方程。而对称分量法以叠加原理为基础，因此从理论上讲，只适用于线性电路。对于电机等非线性系统，把激磁回路按额定电压点作线性化处理，不会带来很大的误差[17]。

设三相电源电压为：

(1)

由对称分量法，令正序分量为

(2)

其中a=ej120°。此时就将三相电压简化为一个用空间向量表示的方程，大大减少方程数量。同理也可得到电流、磁链等的空间向量表达式。

在定子坐标系中，可得到空间向量表示的定、转子的电压、磁链方程[12]：

(3a)

(3b)

将上两式联立，可得：

(3c)

其中：Rs，Rr为定转子电阻；Lm为励磁电感；Ls、Lr分别为定转子自感；p为微分算子；ωr为转子角速度。

2 感应电机不同工作状态的过渡过程

由上面分析可知电机有12个换相瞬间，以A—B—C→B—C→AB—C为例来研究电机在三相和两相导通状态间切换的过渡过程。

2.1 三相同时导通

此时定子电压为对称三相电，可得空间向量为

(4)

对式(4)进行拉氏变换得到：

(5)

由式(5)计算可得

(6)

联立式(5)式(6)，可得

(7)

其中：

(8)

经过以上一系列的推导，得到了在任意初始条件下(三相电源对称)由电源变化引起的定转子瞬态电流的空间向量表示的拉普拉斯变换解析表达式。

2.2 两相导通

假定A相关断，B、C相导通，此时定子电压空间向量为

(9)

其拉氏变换为

(10)

此时，转子电流空间向量表达式不变，同式(6)。将式(10)代入式(5)中，经进一步计算，得到：

(11)

(12)

(13)

同理可得，当B相断开时

(14)

当C相断开时

(15)

这样，就可得到任意一相断开时定转子电流的空间向量表达式。

3 瞬态过程计算

3.1 对三相导通时定转子电流的求解

从两相切换到三相时，电机定转子电流初值均不为零。由式(6)、式(8)得

ωr(cr)=2ω1σ/Xm。

(16)

这样便可得到定转子电流的空间向量表达式：

(17)

(18)

转化到时域形式的定子电流：

同理可得其他相定转子电流。

3.2 对两相导通时定转子电流的求解

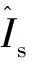
(19)

而转子电流除初值不同外，表达式与前面所得计算结果一致。上述两种情况下，当求得定转子电流后，不难得到电磁转矩为

(20)

由于定转子电流本身就已经非常复杂，二者进行叉乘之后的电磁转矩过于复杂这里不再给出其表达式，关于其计算问题将在以后的研究中继续。

3.3 求解分析

观察定子电流分母表达式的根，我们发现[12]：

1)当转子转速为零时，s2，s3为两个实根，相应的定子瞬态电流为两个衰减的直流；

2)当转子转速介于零和临界转速时，s2，s3将以wr/2的频率发生振荡；

3)当转子转速大于临界转速时，s2，s3的衰减系数保持不变，而振荡频率发生改变。

上述结果是文献[12]在计算感应电机的断电-重合闸问题时得出的。在研究晶闸管供电感应电机低频振荡时，由于没有变频器电感和电容的影响，较容易得出与电机本体相关的结论：

由于感应电机端电压频繁切换于三相对称和两相不对称电压，电机的过渡过程存在类似断电-重合闸的现象，与之不同的是，此时电机只是一相而不是三相同时断电，定转子电流的初值均不为零，导致二者的分析过程也相差甚远。通过对电机在不同工作状态间切换的过渡过程进行计算，得到造成电机低频振荡的因素：电机的不连续供电是造成其低频振荡的主要原因。

感应电机在不同状态之间切换时，定子电压发生突变，由磁链守恒原理，转子中将会产生非周期电流分量来维持穿过磁路的磁链不变；此时，定子电流中出现振荡分量。当电机的转速低于临界转速继续进行不同状态间的切换，定子电流中就会一直存在不断衰减又不断上升的非周期分量，这也就是看到的振荡现象。

3.4 求解过程

晶闸管供电系统下，一个周期内共有12个过渡过程，上面的分析只是以一个三相和两相供电过程为例。上述计算过程都是在假设转速恒定情况下进行的。为与实际情况一致，还需考虑转速变化。具体计算时，每个两相和三相导通状态的定子电压都不同，定转子电流的初值也不相同，编写软件程序来完成计算，其流程如下：

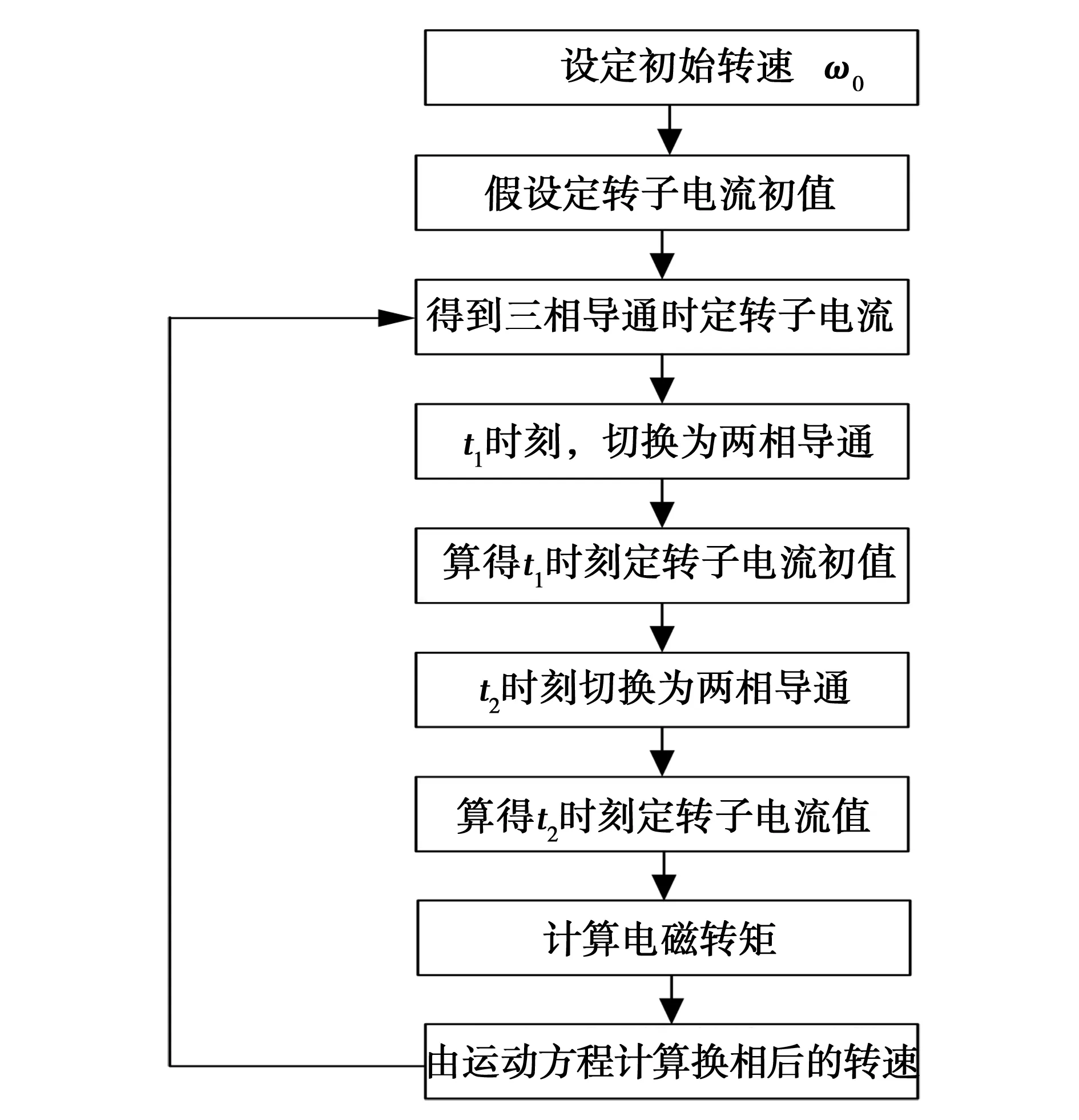
图2 电机过渡过程计算流程图Fig.2 Calculation flow of transit process

上述计算流程中每个过渡过程的总时间为十二分之一个电周期，计算2000个点，总共计算10个周期。

4 仿真和实验研究

由于文献[14]已对晶闸管在50 Hz供电时不同触发角情况下的感应电机振荡问题已进行了初步分析，故不对这些问题进行过多论述，这里，给出导通角接近180°情况下，感应电机在晶闸管低频供电时振荡现象的研究结果。

所用三相感应电机和变频器参数如表1和表2分别所示：

表1 电机参数Table 1 Parameters of motor

表2 变频器参数

图3 主电路拓扑结构Fig.3 Topology structure of main circuit

应用本文计算方法对上述三相感应电动机的空载情况进行计算。经大量理论计算和试验研究发现，在导通角接近180°时，上述感应电机在8～20 Hz范围内都会出现振荡现象，由于篇幅限制，现只对10 Hz情况进行分析说明。图4为空载、10 Hz、导通角接近180°时的A相电流的计算波形和实验结果,对比可知两图吻合较好，由于存在振荡分量，电机相电流的频率不是严格的10 Hz，且振荡电流的幅值较大，是空载电流的10倍左右。另外，由于实际应用中很少有能输出标准正弦波且能变频的电源，所以本实验所用电源为可编程电源。

通过式(16)算得10 Hz时电机的临界转速为130 rpm，所以当电机转速低于临界转速时，定转子电流中会出现振荡分量。但由于定转子电流中还存在其他的非周期分量，所以提取振荡电流分量还需要做进一步的工作。

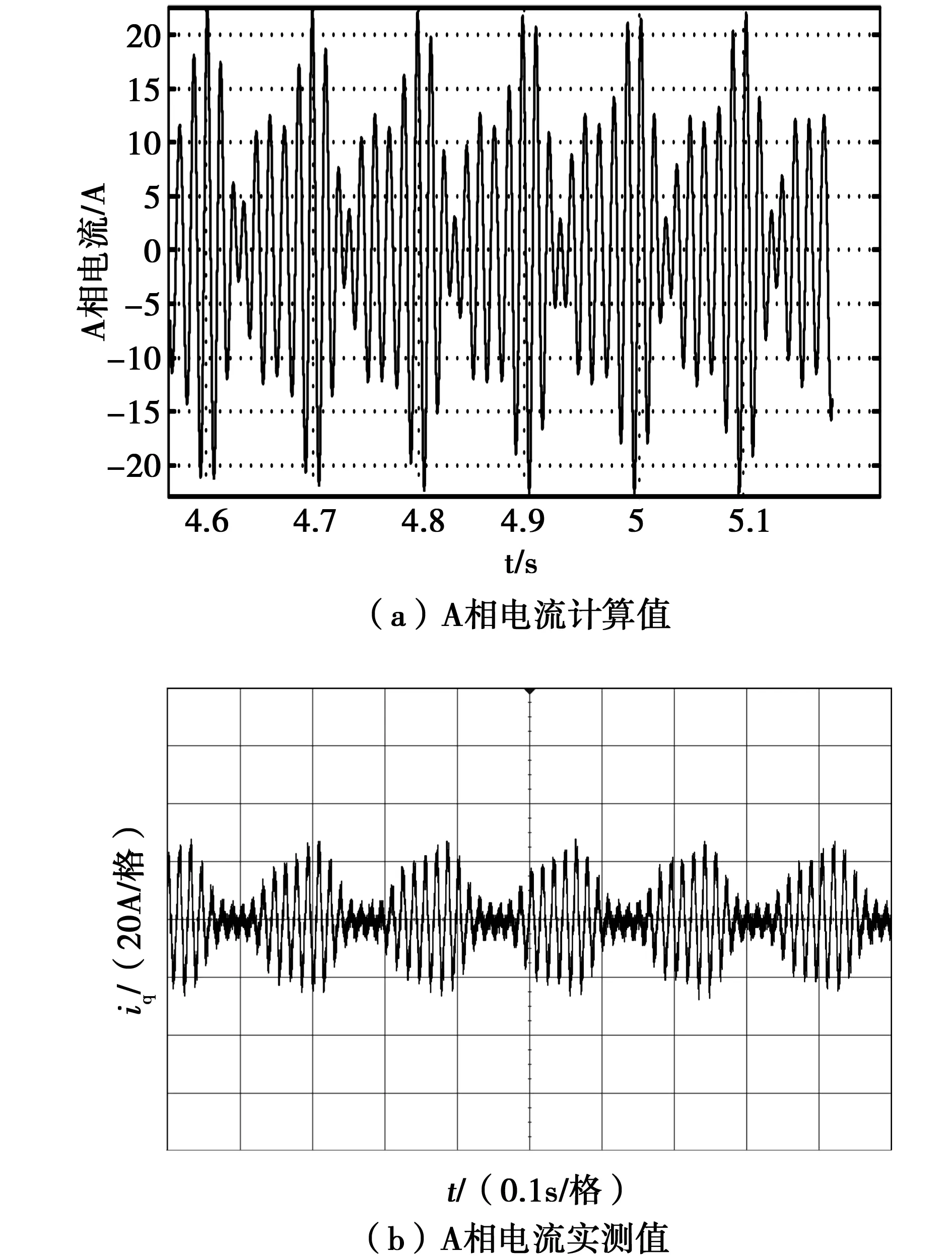
图4 振荡时A相电流的计算值和实验值Fig.4 Computation and experiment result of phase A oscillation current

5 结 论

本文应用对称分量法研究了三相感应电机在晶闸管供电模式下的过渡过程及振荡问题,得到了感应电机在不同通电状态下的定转子电流方程，通过计算以及实验分析，得到结论如下：

1)由于三相感应电机在晶闸管供电模式下频繁切换与三相及两相导通状态，使其端电压具有不连续性，从而在低于其临界转速情况时出现了振荡现象。

2)改变电机的定转子电阻及励磁电感，可以降低电机的临界转速，从而提高其稳定运行范围。

3)现在的感应电机调速系统大都由变频器供电，而本文所研究的系统其过渡过程与变频器供电时有很多相似的地方，所以为下一步对变频器-感应电机系统的低频振荡现象的研究打下基础。

[1] 高景德,张麟征．电机过渡过程的分析理论即分析方法[M]．北京：科学出版社,1983:666-794．

[2] 黄立培．异步电机重投入过程及起动过程的研究[D]．北京：清华大学电机工程系,1982．

[3] Thomas S KEY．Predicting behavior of induction motors during service faults and interruptions[J].IEEE Industry Applications Magazine,1995,1(1):6-11,32.

[4] 汪雄海．电机电源切换冲击扰动机理分析及保护[J]．浙江大学学报(工学版),2002,36(1)：97-100.

WANG Xionghai． Study on transient response due to fast reclosing of the electrical sources of the motor[J]． Journal of Zhejiang University(Engineering Science),2002,36(1):97-100．

[5] 马志云．电机瞬态分析[M]．北京：中国电力出版社,1998:39-40．

[6] Sarma S Mulukutla,Edward M Gulachenski．A critical survey of considerations in maintaining process continuity during voltage dips while protecting motors with reclosing and bus—transfer practices[J]．Transactions on Power Systems,1992,7(3)：265-272．

[7] 潘飞．电动机再起动技术[J]．电工技术杂志,2004(3)：19-23．

PAN Fei．Motor restart technique[J].Electrotechnical Journal,2004(3):19-23．

[8] 李红梅．逆变器供电异步电动机低频振荡及转矩脉动的研究[D]．沈阳：沈阳工业大学,2003．

[9] 严干贵,姜齐荣,蒋霞,等．变频电源驱动下的中高压异步电动机的振荡分析[J]．电力电子技术,2003,37(3) ： 45-48．

YAN Gangui,JIANG Qirong,JIANG Xia,et al．Oscillation analysis of induction motor driven by variable amplitude and frequency voltage source[J]．Power Electronics,2003,37(3)：45-48．

[10] 陆益民．感应电动机分岔现象分析及混沌控制[D]．广州：华南理工大学,2004．[11] 郭云珺,王东,刘德志,等.变频驱动三相感应电机系统稳定性的数学推导与分析[J]．电工技术学报,2010(9)：47-55．

GUO Yunjun,WANG Dong,LIU Dezhi,et al．Mathematical deduction and stability analysis of inverter-fed three-phase induction motor drive system[J]．Transactions of China Electro- technical Society,2010(9)：47-55．

[12] 杨玉磊．三相感应电机断电重合闸瞬态分析与控制方法研究[D].北京：华北电力大学,2008．

[13] 张晓锋.同步发电机整流系统的运行稳定性研究[D]．北京：清华大学,1995．

[14] 王玉峰,马广程,王常虹,等.晶闸管控制感应电机起动过程中振荡现象研究[J].电机与控制学报,2002,6(3)：186-190．

WANG Yufeng,MA Guangcheng,WANG Changhong,et al ．Study of the oscillation in the starting of induction motor controlled by thyristor[J]．Electric Machines and Control,2002,6(3)：186-190．

[15] 曾令全,王志霞,刘耀年．异步电动机无速度传感器再起动方法的研究[J]．电工技术学报,2003,18(2)：53-56．

ZENG Lingquan,WANG Zhixia,LIU Yaonian.Research of speed sensorless restart method for asynchronous motor drive System[J]．Transactions of China Electro- technical Society,2003,18(2)：53-56．

[16] 汤蕴璆,张奕黄,范瑜．交流电动机动态分析[M]．北京：机械工业出版社,2005．

[17] 汤蕴璆,史乃,沈文豹．电机理论与运行[M]．北京：机械工业出版社,2005．

(编辑：张 楠)

Low frequency oscillation mechanism research on induction motors under discontinuous power supply

QIAO Ming-zhong， ZENG Hai-yan， ZHU Peng

(College of Electric Engineering,Naval University of Engineering,Wuhan 430033,China)

In order to avoid influence from inductance and capacitance on the inverter side,symmetrical components theory was introduced to study the oscillation of induction motor supplied by thyristors.This is the simplest discontinuous supply mode,but can give suggestions for more complex situation.The transient process of phase exchange and speed variation were analyzed when the motor was powered by 2 and 3-phase voltage,and the space-vector expression of stator and rotor current during different transient process was analyzed,and its time domain solution was given.The cause of oscillation was found out when induction motor worked at discontinuous power supply,and explanation of oscillation was presented in the view of the motor itself.A 3-phase induction motor was analyzed using the theory given above.It proves that calculation results are very close to the measurement results,and this method can be the basis for transient process study of induction motor supplied by inverters.

induction motor；oscillation；discontinuous power supply；transient process

2015-01-08

国家自然科学基金(51277177，51407188，51507183)

乔鸣忠(1971—)，男，博士，教授，博士生导师，研究方向为电力电子与电力传动； 曾海燕(1983—)，女，硕士，助教，研究方向为电力电子与电力传动； 朱 鹏(1984—)，男，博士，讲师，研究方向为电力电子与电力传动。

曾海燕

10.15938/j.emc.2017.03.005

TM 346

A

1007-449X(2017)03-0032-06