利用导数解决实际生活中的问题

乌仁其其格

（赤峰学院 数学与统计学院，内蒙古 赤峰 024000）

利用导数解决实际生活中的问题

乌仁其其格

（赤峰学院 数学与统计学院，内蒙古 赤峰 024000）

导数是高等数学中重要的基础性内容，而且在实际生活中有着广泛的应用，利用导数可以求出实际生活中的某些最值问题和经济问题.如利润最大、生产效率最大、用料最少、耗油量最少等问题.

导数；最值问题；经济问题

1 最值问题

1.1 最大利润问题

例1上海某公共汽车公司举办市内观光旅游.若票价为每人40元，则一周游客约1000人；若票价为每人30元，则一周游客约1400人.假定游客人数x与票价p是线性关系，那么为了使一周的收益最大，票价应定为多少？又若举办此项观光旅游的一周成本为C（x）=20000+10x(元)，问为使一周的利润最大，票价应定为多少？

解首先列出需求方程，即票价p与人数x应满足的线性方程.由直线的两点式方程，即有

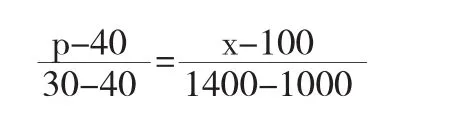
由此得到

从而收益为

边际收益为

由于R(x)为开口向下的抛物线，所以当边际收益为零时，收益达到最大值，即当x=1300时，R(x)有最大值.此时的票价即可以从x=1300代入（1）式得到：

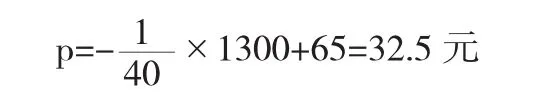
当考虑利润时，我们得到一周的利润为

所以边际利润为

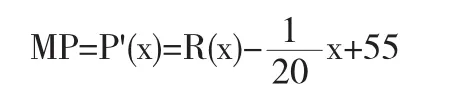
P(x)的图形也是开口向下的抛物线，所以，当边际利润为零时，利润达到最大值，即当x=1100时，P(x)有最大值.此时的票价以x=1100代入（1）式得到:

根据以上分析，结论是32.5元的票价极可能带来最大的每周收益，但37.5元的票价极可能带来最大的每周利润. 1.2 费用最少问题

例2工厂A到铁路线的垂直距离为20km，垂足为B.在铁路线上距离B 100km处有一个原料供应站C，现要在铁路B、C之间某处D修建一个原料中转站，再由车站D向工厂修一条公路.如果已知每千米的铁路运费与公路运费之比为3：5，那么D应选在何处，才能使原料供应站C运货到工厂A所需的运费最省？

解这样的最值问题，首先要合理建模，使问题获解.

解设B、D之间的距离为xkm，

则|AD|2=202+x2，|CD|=100-x

如果公路运费为a元/千米，那么铁路运费为3a/5元/千米.

所以从原料供应站C途经中转站D到工厂A所需的总运费

解得x1=15，x2=-15（不符合实际意义，故舍去），

于是x1=15是函数y在定义域内的唯一驻点，所以x1=15是函数y的极小值点，而且也是函数y的最小值点.由此可知，车站D建于B、C之间并且与B相距15km处最可省运费.

1.3 容积最大问题

例3在一块边长为2a的正方形铁皮上，四角各截去一个边长为x的小正方形，用剩下的部分做成一个无盖的盒子（见图2-9），试问当x取什么值时，它的容积最大，其值是多少？

解由于小正方形的边长为x，故盒子底边长为2a-2x，它的容积为

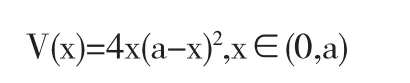
由

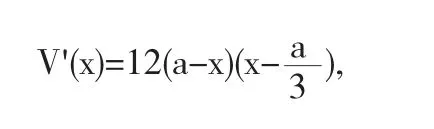
解V'(x)=0得驻点x1=a,x2=a/3.由于当x1=a时，表示铁皮完全被截去，这是容积为零，不合题意，故V(x)在区间(0,a)内只有唯一的驻点x2=a/3，另一方面，根据此问题的特点可以判定V(x)一定有最大值.因此当x2=a/3时，V(x)取的最大值，其值为

例4用总长为14.8m的钢条做一个长方体容器的框架，如果所做容器的底面的一边比另一边长0.5m.那么高是多少时容器的容积最大?并求出它的最大容积.

解设容器底面矩形短边长为xm，则另一边长为(x+0. 5)m，高为=(3.2-2x)m.由(3.2-2x)＞0且x＞0，得0＜x＜1.6.设容器的容积为y m3,则y=x(x+0.5)(3.2-2x).令 y'=-6x2+4.4x+1.6=0，则x=1或x=（舍去）.

从而，在定义域（0,1.6）内只有在x=1处使得y'=0.由题意，若x过小（接近0）或过大（接近1.6）时，y的值很小（接近0），因此，当x=1时，y取得最大，y最大=-2+2.2+1.6=1.8.这时，高为3.2-2×1=1.2.

故当容器的高为l.2m时，容器的容积最大，最大值为1.8m3.

1.4 费用的节省

例5某种型号的小型客车在匀速行驶中每小时耗油量y（升）与行驶速度x（千米/小时）的函数解析式可以表示为：y=x+8(0＜x≤120)已知甲、乙两城市相距100千米.试问：当汽车以多大的速度匀速行驶时，从甲城市到乙城市耗油最少？

解依据题意，得：

依题意得

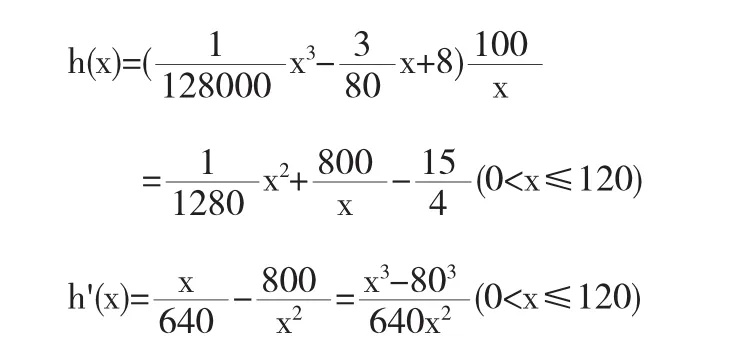
令h'(x)=0,得x=80.

当x∈(0,80)时，h'(x)＜0,h(x)是减函数；

当x∈*80,120)时，h'(x)＞0,h(x)是增函数；

由导数的极值判别定理可知，当x=80时，h(x)取到极小值h(80)=11.25

由于h(x)在(0,120]上有且仅有一个极值，所以它是最小值.当汽车以80千米/小时的速度匀速行驶时，从甲城市到乙城市耗油最少.

1.5 速度问题

例6求自由落体在时刻t=1(秒)时的瞬时速度v.

解

当t=1时，v=g.

2 经济问题

定义1设函数y=f(x)是一个经济函数且在点x处可导，则称导数f'(x)是f(x)的边际函数，f'(x)在x0处的值f'(x0)是边际函数值.

定义2总成本C=C(Q)的导数C'称为边际成本，平均成本的导数称为边际平均成本.

例7设某种产品的总成本函数C(Q)=2000+45Q+0. 02Q2，Q∈[0,1000]，试求：

（1）当产量为100吨时的总成本；

（2）当产量为100吨时的平均成本；

（3）当产量从100吨增加到200吨时，总成本的平均变化率；

（4）分别求当产量为100吨和200吨时的边际成本.

解（1）当产量为100吨时的总成本

C(100)=2000+45×100+0.02×1002=6700.

（2）当产量为100吨时，平均成本

（3）当产量从100吨增加到200吨时，

所以总成本的平均变化率为

（4）边际成本函数

所以

这说明当产量为100时，再增加一个单位产品的生产，总成本将增加49；当产量为200时，再增加一个单位产品，总成本将增加53.

3 结束语

上面的讨论中我们可以得知，导数的应用渗透到社会领域的方方面面.本文通过举例的方式利用导数解决很多的实际问题，最优化问题具有很强的应用性，如需求函数、供给函数、消费函数、生产函数、投资函数等等，在生活中均得到广泛应用，通过运用数学方法解决生活问题，实现方法最优化、计划最优化、过程最优化、结果最优化等等.最优化问题不管是在提高自身思维能力方面，还是在平时生活处理问题，都是大有益处的.它使我学到了如何运用数学方法解决生活问题，实现方法最优化，计划最优化，过程最优化，结果最优化等.最优化问题不仅具有趣味性，而且由于解题方法灵活，技巧性强，因此对于开阔解题思路，增强数学能力，很有益处，但解决这类问题最优化，实践或不可缺的.

〔1〕同济大学应用数学系.高等数学[M].北京：高等教育出版社，2006.

〔2〕张娟.浅谈导数在实际生活中的应用[J].科技信息，2010（19）.

〔3〕柯善文,范斌,李杰.浅谈导数在实际生活中的应用[J].大众科技，2011（03）.

〔4〕黄绍东.浅谈导数在实际生活中的应用[J].河北能源职业技术学院学报，2014（04）.

〔5〕刘朝霞.浅谈导数在实际生活中的应用[J].科技视界，2015（21）.

〔6〕江霞平.导数在生活中的应用举例 [J].科技资讯，2013（15）.

O172

A

1673-260X（2017）02-0013-03

2016-12-22