双正态正态区间估计和假设检验的拓广
2017-03-29刘国祥
刘国祥
(赤峰学院 数学与统计学院,内蒙古 赤峰 024000)
双正态正态区间估计和假设检验的拓广
刘国祥
(赤峰学院 数学与统计学院,内蒙古 赤峰 024000)
本文给出双正态独立总体下区间估计和假设检验的拓广,主要推广了总体均值的线性函数的区间估计和方差比不是1的假设检验方法.
正态分布;独立性;区间估计;假设检验;数学期望;方差
一般的概率论与数理统计教材[2][3][4],都给出两个正态总体下,均值差和方差比的区间估计和假设检验.现在将它们拓广为一个数学期望是另一个的线性函数和两个方差比不是1的情况的,给出置信区间估计和显著性假设检验的方法.
多数教材上给出的两个正态总体下统计量的基本性质是:
引理1(两正态总体下统计量的基本性质)假定X,Y是相互独立的两个总体,且
总体X~N(μ1,σ12),样本为(X1,X2,…,Xn1),
总体Y~N(μ2,σ22),样本为(Y1,Y2,…,Yn1).
那么:

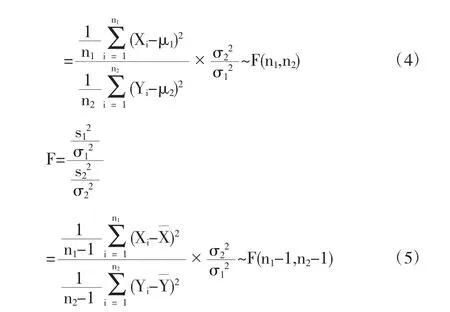
其中(1)是在已知方差,估计和检验均值差时用的.(2)是在未知方差,估计和检验均值差时用的,但是已知σ1=σ2=σ.(3)[2]是在未知方差,估计和检验均值差时用的,但是已知σ12≠σ22.(4)是在已知均值,估计和检验方差比时用的.(5)是在未知均值,估计和检验方差比时用的.
定理1假定X,Y是相互独立的两个总体,且
总体X~N(μ1,σ12),样本为(X1,X2,…,Xn1),
总体Y~N(μ2,σ22),样本为(Y1,Y2,…,Yn1),a,b∈R.
那么:在σ12,σ22已知时:
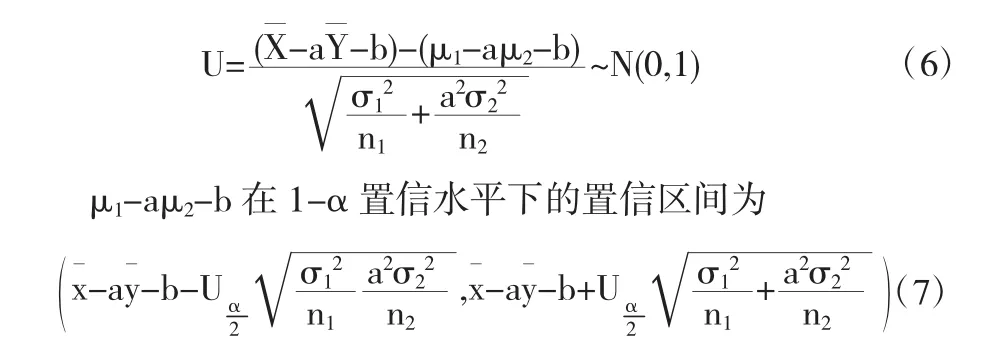
证明由于假定X,Y是相互独立的两个总体,且总体X~N(μ1,σ12),样本为(X1,X2,…,Xn1).总体Y~N(μ2,σ22),样本为(Y1,Y2,…,Yn2).a,b∈R.
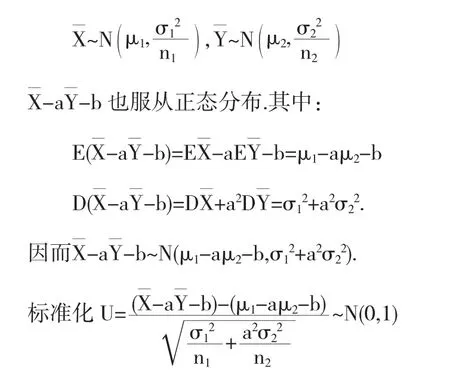
相应地,容易得到μ1-aμ2-b在1-α置信水平下的置信区间为
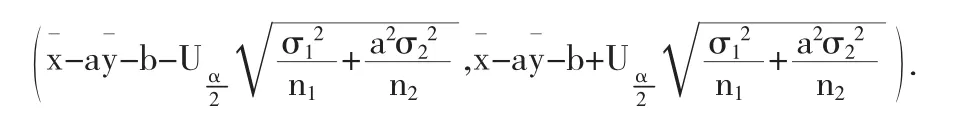
根据区间估计和假设检验之间的关系,可以得到原假设:
H0:μ1=aμ2+b的显著性假设检验.
定理2假定X,Y是相互独立的两个总体,且
总体X~N(μ1,σ12),样本为(X1,X2,…,Xn1),
总体Y~N(μ2,σ22),样本为(Y1,Y2,…,Yn2).a,b∈R.
那么:在σ12,σ22未知时,在σ12=σ22=σ2下,有
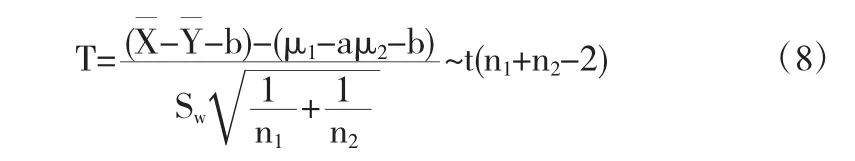
μ1-aμ2-b在1-α置信水平下的置信区间为
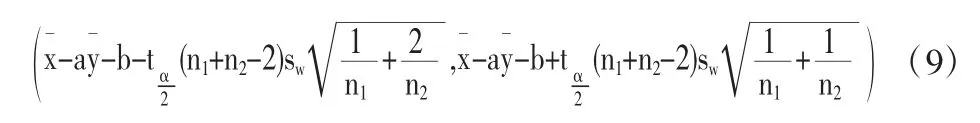
证明由于假定X,Y是相互独立的两个总体,且总体X~N(μ1,σ12),样本为(X1,X2,…,Xn1),总体Y~N(μ2,σ22),样本为(Y1,Y2,…,Yn2).a,b∈R.
设Z=aY+b,那么,X,Z也独立.
由于方差未知,那么:
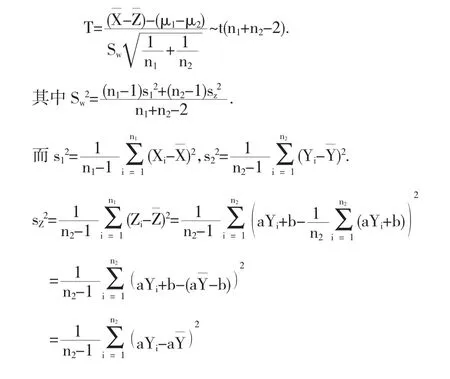
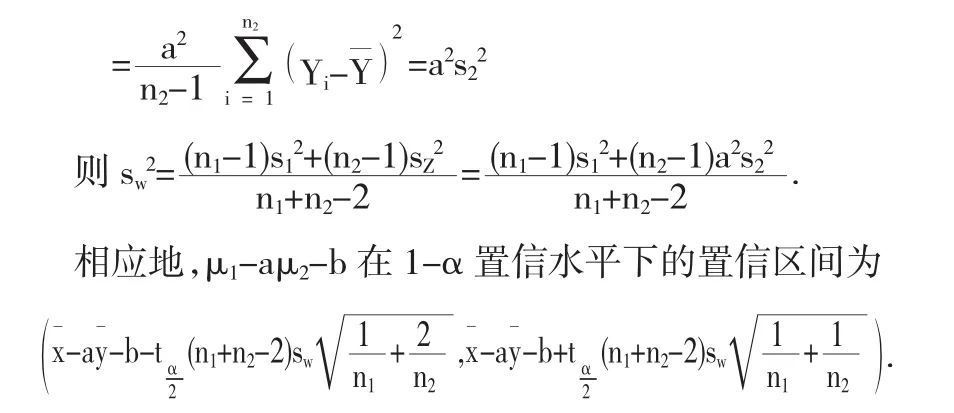
根据引理1之(4)、(5),容易得到:
引理2假定X,Y是相互独立的两个总体,且总体X~N (μ1,σ12),样本为(X1,X2,…,Xn1),总体Y~N(μ2,σ22),样本为(Y1,Y2,…,Yn2).那么:
在μ1,μ2已知时,方差比在1-α置信水平下的置信区间为:
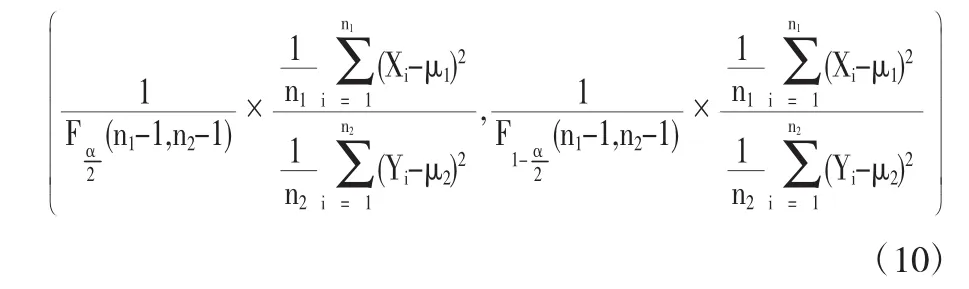
在μ1,μ2未知时,方差比在1-α置信水平下的置信区间为:

关于假设检验,一般文献都给出σ12=σ22,或者说的检验.那么我们如果要检验=a,未见文献论述.下面拓广假设检验的应用.
定理3假定X,Y是相互独立的两个总体,且总体X~N (μ1,σ12),样本为(X1,X2,…,Xn1),总体Y~N(μ2,σ22),样本为(Y1,Y2,…,Yn2).a,b∈R+.那么:
关于原假设H0:σ12=aσ22,或者
在μ1,μ2已知时,如果1属于置信区间(10),则,接受原假设,否则就拒绝.
在μ1,μ2未知时,如果a属于置信区间(11),则,接受原假设,否则就拒绝.
根据区间估计和假设检验之间的关系,可以证明[3],这里略去.
关于两个正态总体的单侧区间估计和单侧假设检验的相应结论,容易列出.
例 1[5]甲种产品长度X~N(μ1,5),乙种产品长度Y~N (μ2,1),甲乙独立.现在在甲种产品中抽取4只,测得长度分别是:4.0,4.2,4.6,5.0.在乙种产品中抽取5只,测得长度分别是:2.0,2.3,2.1,2.5,2.8.能否认为甲种产品长度是乙种产品长度的2倍?显著水平α=0.05.
这是两个正态总体均值的假设检验问题,已知方差σ12=5,σ22=1.
根据定理1,提出原假设和备选假设H0:μ1-2μ2=0,H1:μ1-2μ1≠0.
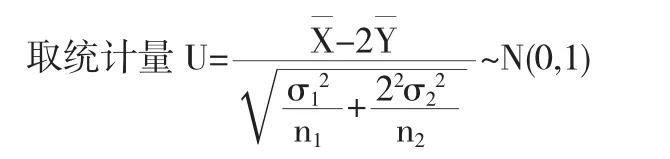
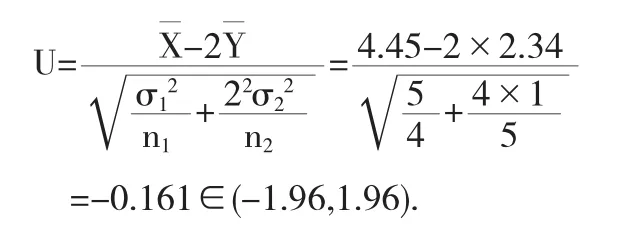
所以接受原假设,也就是可以认为甲种产品长度是乙种产品长度的2倍.
相应地,容易得到μ1-2μ2在1-α=1-0.05=0.95置信水平下的置信区间为
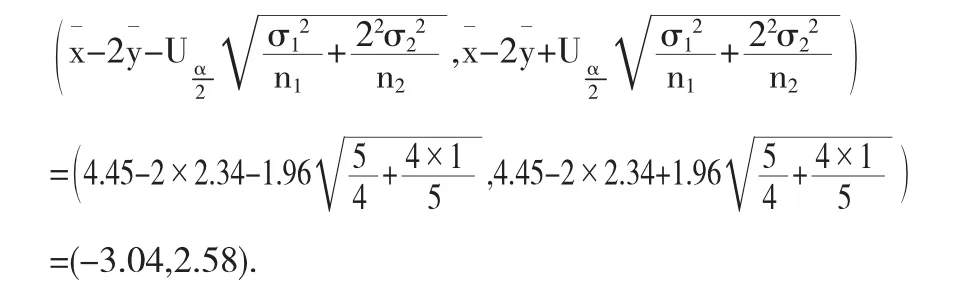
1∈(-3.04,2.58),所以可以认为μ1-2μ2=0,或者说μ1=2μ2.
注意,这里置信区间比较大的原因是题目中数学期望比较小,而方差比较大的缘故.
例2[4]某自动机床加工同类型套筒,假设套筒的直径服从正态分布,现在从两个班次的产品中个抽检5个套筒,测量它们的直径,得如下数据:
A班:2.066,2.063,2.068,2.060,2.067.
B班:2.058,2.057,2.063,2.058,2.060.
这就是(11)的情况,计算得:
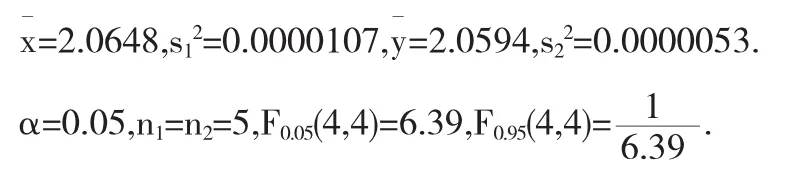
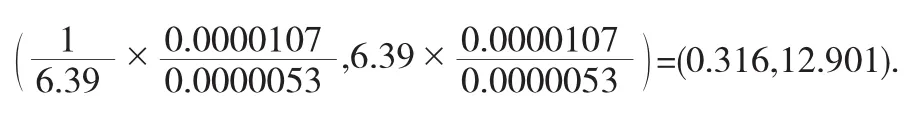
这个问题改为,其它条件不变,问在α=0.10时,
能否接受σ12=0.5σ22?,0.5∈(0.316,12.901),当然接受.
能否接受σ12=σ12?,1∈(0.316,12.901),当然接受.
能否接受σ12=5σ22?,5∈(0.316,12.901),当然接受.
能否接受σ12=10σ22?,10∈(0.316,12.901),当然接受.
能否接受σ12=20σ22?,20∈(0.316,12.901),当然不能接受.
一般情况下,方差和方差比的变动都比较大,出现这样结果不奇怪.
〔1〕刘国祥,张晓丽,杨永霞,等.应用型人才培养模式下概率论与数理统计课程改革探索与实践[J].赤峰学院学报(自然科学版),2014(12).
〔2〕贾俊平,何晓群.统计学(第六版)[M].北京:中国人民大学出版社,2015.160-189.
〔3〕浙江大学,盛骤,谢式千,潘承毅.概率论与数理统计(第四版)[M].北京:高等教育出版社,2008.192-193.
〔4〕武汉大学数学与统计学院,齐民友,刘禄勤,龚小庆,王文祥.概率论与数理统计[M].北京:高等教育出版社,2002.190-193.
〔5〕硕士研究生入学统一考试数学命题研究中心,数学复习辅导——概率论与数理统计[M].上海:上海交通大学出版社,2010.128.
〔6〕刘国祥,杨永霞,张晓丽,等.基于应用型人才培养模式下的贝叶斯公式教学[J].赤峰学院学报(自然科学版),2015(01).
O212.1
A
1673-260X(2017)02-0010-03
2016-12-10
