一种新的基于身份的代理盲签名方案

梁林

（安徽农业大学 经济技术学院，安徽 合肥 230011）

一种新的基于身份的代理盲签名方案

梁林

（安徽农业大学 经济技术学院，安徽 合肥 230011）

研究一个签名方案，指出该方案的代理密钥生成阶段存在安全隐患，不法者可以伪造原始签名者的签名或授权.本文为克服这一困难，先根据椭圆曲线上的双线性对的特性，再通过增加盲因子的方法，设计了一个更安全可靠的基于身份的代理盲签名方案.

代理盲签名；双线性对；基于身份；安全性

1 引言

盲签名[1]的概念是Chaum在1983年时第一次提出，M. Mambo在1996年提出了代理签名[2]的概念.将代理签名与盲签名相结合形成了代理盲签名[3].因为传统的公钥密码体制是在公钥结构证书PKI的基础上来形成的，而在证书的管理过程中，尤其是在密钥的管理上，是需要花费很高的计算成本和存储消费的.为了简化传统公钥密码体制，减少开支，1984年Shamir提出了一种新思想，基于身份的密码系统[4].基于身份的密码体制的优越性在于，它不需要保存用户的公钥证书，用户的公钥是可以根据自己的身份信息直接计算出来的，而私钥则是由可信中心来统一生成得到.在基于身份的密码体制的基础上，人们又利用椭圆曲线的双线性对，构造出基于身份的代理盲签名方案，基于身份的密码体制已经成为密码学的一个新研究热点.

文献[5]就是通过利用椭圆曲线上的双线性对，构建了一个基于身份的代理盲签名方案.但分析后发现，在方案的代理密钥生成阶段却存在着安全隐患，不法者可以伪造原始签名者的签名或授权.为克服这一困难，本文利用计算离散对数的困难性，根据椭圆曲线上的双线性对所具有的特殊性质，设计了一个安全可靠的基于身份的代理盲签名方案.

2 双线性映射

设G1、G2是循环群，q为它们的阶（q是一个大素数）.G1是加法循环群，G2是乘法循环群，设e：G1×G1→G2是一个双线性映射，它满足下面三个性质：

（1）双线性：∀P,Q∈G1,a,b∈Zq,e(aP,bQ)=e(P,Q)ab；

（2）非退化性：存在P,Q∈G1,使得e(P,Q)不等于G2的单位元；

（3）可计算性：对任意P,Q∈G1存在有效的算法计算e (P,Q).

在双线性对中存在以下几个数学难题：

（1）DLP（Discrete Logarithm Problem）：设P,Q∈G1求解n∈Zq*，使得Q=nP.

（2）CDHP（Computational Diffie-Hellman Problem）：设P∈G1,a,b∈Zq*，给定P,aPO,bP,计算abP.

（3）DDHP（Decision Diffie-Hellman Problem）：设 P∈G1，a,b,c∈Zq*,给定P,aP,bP,cP,判定c≡abmodq.是否成立.

（4）GDHP（Gap Diffie-Hellman Problem）：在循环群G1中，DDHP是易解的，即在多项式内DDHP是容易求解的；而CDHP却是比较复杂的，目前还没有可行的算法来求解CDHP.此时称循环群G1为GDH群.

3 文献[5]方案描述

3.1 系统参数设置

设G1、G2是循环群，q为它们的阶（q是一个大素数）.G1是加法循环群，G2是乘法循环群.

HGC首先选择P∈G1，设e:G1×G1→G2为一个双线性映射.定义密码学上3个Hash函数：H1(·):{0,1}*→G1，H2(·): {0,1}*×G2→Zq*，H3(·):G1→Zq*，然后KGC再选择t∈RZq*，计算Ppub=tP，其中t保密存储，称为系统主密钥.

公开系统参数：params={G1,G2,w,q,P.Ppub,H1(·),H2(·),H3(·)}.

方案参与者分别为：原始签名者A，代理签名者B和盲签名的持有者C.

3.2 密钥提取

A与B先将自己的身份信息IDA,IDB提交给KGC，然后由KGC计算他们的公钥/密钥对，分别为PKA=H1(IDA)，SKA=tPKA，PKB=H1(IDB)，SKB=tPKB.最后，再将这些信息安全地发送给A与B.

3.3 代理密钥生成

先由原始签名者A创建一个许可证W，主要包括参与者的身份信息，代理期限，签名文件的范围等.

3.3.1 原始签名者A计算：

然后将(W,SW)发送给代理签名者B.

3.3.2 代理签名者B计算并验证：

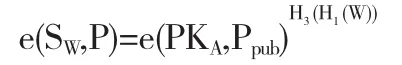
是否成立.如果是成立的，可以计算得到代理签名密钥：

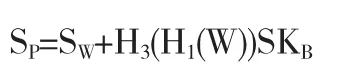
3.4 代理签名生成

3.4.1 代理签名者B选择P1∈G1，计算K=e(P1,P)，然后将(K, W)发送给盲签名的持有者C.

3.4.2 盲签名的持有者C选择P2=∈G1，b∈RZq*,计算

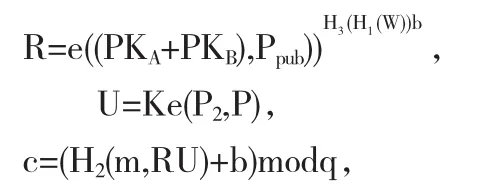
然后将c发送给代理签名者B.

3.4.3 代理签名者B计算S=cSp+P1，然后将S发送给盲签名的持有者C.

3.4.4 盲签名的持有者C计算S'=S+P2,c'=c-b，

则σ(m)=(S',c',m,W)为消息m的基于身份的代理盲签名.

3.4.5 签名验证验证下式

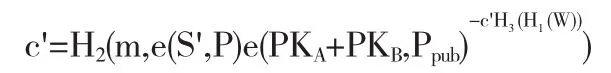
是否成立.若成立，说明签名σ(m)=(S',c,m,W)是有效性的.若不成立，则什么签名是无效的.

4 本文基于身份的代理盲签名方案

4.1 文献[5]方案安全性分析

在文献[5]描述的代理密钥生成过程中，由A先计算一个短签名SW=H3(H1(W))SKA，然后再将(W,SW)发送给B.在这个过程中，由于W,H1,H3是公开已知的，因此B是可以计算出H3(H1(W))∈Zq*，并且B又已知SW∈G1，所以可以容易计算出SKA∈G1.也就是说，B是能够计算出H3(H1(W))∈Zq*的逆运算H3(H1(W))-1∈Zq*，进而可以计算出H3(H1(W))-1SW=H3(H1(W))-1H3(H1(W))SKA=SKA，也就是说A的授权或签名是可以伪造的.因此，在文献[]描述的签名方案中存在着安全问题.

4.2 方案设计描述

为了克服文献[5]中的安全问题，设计了下面的新方案：

4.2.1 系统参数设置

本文系统参数设置与文献[5]系统参数设置基本相同，但需要将第三个哈希函数进行更改，由原来的H3(·)G1→Zq*改成H3(·):{0,1}*→Zq*.

4.2.2 密钥提取

A与B先将自己的身份信息IDA,IDB提交给KGC，然后由KGC计算他们的公钥/密钥对，分别为PKA=H1(IDA)，SKA=tpKA，PKB=H1(IDB)，SKB=tpKB.最后，再将这些信息安全地发送给A与B.

4.3 代理密钥生成

A首先需要创建一个授权证书W，其中应该包括A和B的身份信息、授权关系以及授权使用权限等内容.

4.3.1 A随机选择rA∈RZq*，再计算

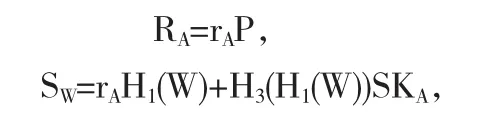
然后将(W,SW,RA)发送给B.

4.3.2 B收到(W,SW,RA)后验证

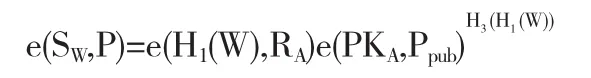
若上式成立，计算得到代理签名者B的代理盲签名密钥：

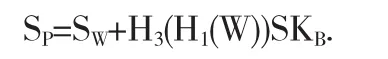
4.4 代理签名生成

4.4.1 B随机选择P1∈G1，计算

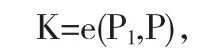
然后将(K,W,RA)发送给C.

4.4.2 C随机选择P2∈G1,b∈RZq*，计算

然后将c发送给B.

4.4.3 B收到c后，计算

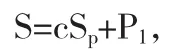
再将S发送给C.

4.4.4 C接收到S后，计算

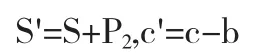
则σ(m)=(S',c',m,W,RA)为消息m的基于身份的代理盲签名.

4.4.5 签名验证

在获得消息m的签名σ(m)=(S',c',m,W,RA)后，验证者就可以通过下式

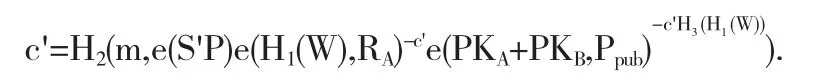
对签名进行验证，验证其是否有效.

4.3 安全性分析

4.3.1 可验证性

从代理签名σ(m)=(S',c',m,W,RA)的生成过程来分析，我们可以计算

所以，代理签名是可验证的.

4.3.2 不可伪造性

因为由KGC保存着主密钥t，要通过Ppub=tp得到t，也就是破解DLP，而DLP是在目前是无法破解的.所以，没有B的密钥(P1,SKB)和代理密钥Sp，他的签名是无法伪造的.

4.3.3 盲性

C将信息m盲化c成是通过以下两个步骤来实现的：

(1)C随机选择P2∈G1,b∈RZq*，计算

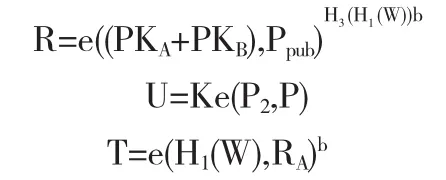
(2)C再利用b对消息m进行盲化：

显然，在不知道P2,b的情况下，B是无法通过上面式子获得c与m之间的联系的.所以方案符合盲性要求.

4.3.4 不可否认性

因为B在建立代理盲签名时已经将他自己的身份信息嵌在代理密钥中，所以代理盲签名一旦生成，他就不能向A否认.

4.3.5 可区分性

签名验证时，由于授权证书W,PKA,PKB都是需要使用的，所以代理盲签名与一般的签名是可以区分的.

4.4 性能分析

本文主要从方案的计算复杂性方面来分析，并与参考文献[5]进行比较：

表4.1 本文方案与文献[5]方案的计算复杂性比较

表中Pa表示双线性对操作，Pm表示G1上的标量乘法，Ad表示G1上的点加操作，ExG2表示G2上的指数运算，MuG2表示G2上的标量乘法，Hs表示哈希函数.计算过程中，Pa的计算是最耗时的，其次是Pm.另外考虑到双线性对e((PKA+ PKB),Ppub)可进行预计算，因此计算复杂性暂时不考虑.

所以，从表4.1可以得到，文献[5]方案的计算复杂度大约是4Pa+3Pm数量级，本文方案的计算复杂度大约是6Pa+ 3Pm数量级，在代理密钥生成阶段和签名验证阶段各增加了1Pa，代理签名阶段的计算复杂度没变.所以本文方案比文献[5]方案的计算复杂度略高些.

再将本文方案与其他方案从计算复杂性方面进行分析，结果如下：

表4.2 本文方案与其他方案的计算复杂性比较

从表4.2可以得到，文献[6]方案和文献[7]方案的计算复杂度分别大约是7Pa+7Pm数量级和3Pa+8Pm数量级，而本文方案的计算复杂度大约是6Pa+3Pm数量级.很明显，本文方案的计算复杂度比这两个方案的计算复杂度都低.

5 结束语

综上所述，为克服文献[5]方案中代理密钥生成阶段存在的安全隐患，本文通过增加盲因子的方法，构建了一个新的基于身份的代理盲签名方案.增加盲因子可以有效地提高代理密钥的安全性，以此来保证方案的安全性.因为在代理密钥生成过程中增加盲因子了，所以计算复杂度就要比文献[5]方案要略高些，但与其他一些方案相比，计算复杂度依然还是较低的.

〔1〕Chaum D.Blind signatures for untraceable payments[C] //Proc of Advances in Cryptology Crypto.New York: Springer-Verlag,1982:199-203.

〔2〕Mambo M,Usdua K,Okamoto E.Proxy signatures: Delegation of the power to sign message[J].IEICE Trans on Functional,1996,E79-A(9):1338-1354.

〔3〕Lin W D,Jan J K.A security personal learning tools using a proxy blind signature scheme[C].Proceedings of International Conference on Chinese Language Computing.USA:Chinese Language Computer Society Knowledge Systems Insitute,2000,273-277.

〔4〕Shamir A.Identity-based cryptosystems and signature schemes[A].Blakley G R,Chaum D.Advancesin Cryptologu:CRYPTO1982[C].Berlin:Springer,1984,47-53.

〔5〕陈玲玲，亢保元，张磊.一种高效的基于身份的代理盲签名方案，华东交通大学学报，2008,25（1）：113-116.

〔6〕Dong Z,Zheng H,Chen K F,et al ID-based proxy blind signature[A].Proceedings of the 18tn International Conferences on Advanced Information Networking and Applications (AINA 2004)[C].Los Alamippos:IEEE Computer Society,2004.380-383.

〔7〕Lang W M,Tan Y M,Yang Z K,et al.A new efficient ID-based proxy blind signature scheme[A].Proceedings of the Ninth Internations(ISCC 2004)[C].Los Alamippos:IEEE Computer Society,2004.407-411.

TP309

A

1673-260X（2017）02-0022-03

2016-09-07

安徽省质量工程（2014jyxm666）