通过设问激发学生的探究意识
2017-03-29毛燕玲
毛燕玲
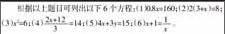

摘 要:在新课程标准实施的今天,教师在数学课堂上进行有效的“设问”,是发挥教师主导作用、体现“学为中心”的重要手段。新课标中指出:“教师应激发学生的学习积极性,向学生提供充分从事数学活动的机会,帮助他们在自主探索和合作交流的过程中真正理解和掌握基本的数学知识与技能、数学思想和方法,获得广泛的数学活动经验。”
关键词:设问;探究意识;学为中心
一、在关键处设问
数学教学中常常出现知识交叉的情况,此时各知识点会互相重叠、覆盖,使学生无法理清脉络,所以我们把“设问之矛” 投向这里,通过学生的思辨进行概括、归纳和比较,以点带面,积极建构。在小学的基础上学生已经能够利用一些常见的等量关系列出方程,而且这节课除了是这章的起始课,同时也是初中阶段各类方程的起始课,所以一开始就让学生列出各种不同类型的方程,通过对比,激发学生对本节课重点,即一元一次方程概念中的分类点的理解。
根据数量关系列方程:
(1)一件衣服按8折销售后售价为160元,求这件衣服的原价。设衣服原价为x元,可列方程: 。
(2)一个长方形的长为3,周长为8,求长方形的宽。设宽为x,则可列方程: 。
(3)一个正方形的面积为6,求正方形的边长。设正方形的边长为x,则可列方程: 。
(4)小强、小杰、张明参加投篮比赛,每人投了20次,小强投进10个,小杰比张明多投进2个。若三人平均每人投进14个球,求张明投进几个球。
设张明投进x个球,则可列方程: 。
(5)小明去文具店买了4支圆珠笔和3支铅笔,共花了15元。设圆珠笔的单价为x元,铅笔的单价为y元,则可列方程: 。
(6)一个数与1的和等于这个数的倒数,求这个数。设这个数为x,则可列方程: 。
问题1:目前为止,代数式中我们重点学习了整式,那这里的方程左右两边都是整式吗?
问题2:我们把代数式里的对象进行分类,那我们列的这些方程也能根据某个标准进行分类吗?(小组讨论交流)
学生呈现分类角度:可以根据未知数个数分;可以根据次数分;可以根据方程左右两边是不是整式分。
二、在“无疑”处设问
有些概念、定理貌似无疑问,其实有重、难点隐含在里面,教师要及时发现,有效解决。比如,本节课的重点之一是对一元一次方程的解的定义的理解及应用,也许这是很显然、很直接的事情,但怎么让学生在这里能理解透彻并且培养出举一反三或举三反一的能力,还是需要对该概念有一定的挖掘。
问1:要解决实际问题,我们还得求出x。比如2(3+x)=8,你知道宽是多少了吗?
生答:是1。
问2:你怎么知道1就是宽?
生答:2(3+1)=8。
问3:宽会是2吗?为什么?
生答:2(3+1)≠8。
问4:那你觉得我们要找的未知数的值应该满足什么条件?
生答:这个未知数的值应该能使该方程左右两边的值相等。
三、在思维提升处设问
在中学的数学教学中,有些教材可以进行逆向思维、变式思维的训练,通过设问,培养学生思维的广阔性、变通性、独创性,以便更好地发展学生的智能。如教学一元一次方程方程的解,除了让学生掌握检验一个未知数的值是不是方程的解,不妨趁此机会训练学生的逆向思维,即已知未知数的值,写出符合该值的一元一次方程。甚至在学生已经写好的方程的基础上进行变式,引进含两个字母的方程的相关问题。
问1:刚才大家都是检验一个未知数的值是不是已知方程的解,现在请你写出满足解是x=-2的一元一次方程。
生答:2x=-4。
问2:我们把这个方程变式:a-2x=-4,且x=-2还是关于x的一元一次方程a-2x=-4的解,你能求出a的值吗?
生答:把x=-2代入a-2x=-4,得a+4=-4,所以a=-8。(该问题的解决方式还是归结为把两个未知数的问题转化成一个未知数的问题)
问3:为什么a=-8?
生答:把a=-8代入a+4=-4,该方程左右两边相等。
四、在小结处设问
课堂小结不仅是一个教学环节问题,也不仅是一个教学形式问题,而是一个教学的發展问题。课堂小结在课堂教学中往往起着提纲挚领、画龙点睛的作用,它通常是指向本节课的基础知识和思想方法及关键点,所以教师要精心设问,刺激学生主动探索的意识和自主学习的习惯,从而可以不断提高数学课堂效率。
问1:通过前面的学习,你知道怎么判断一个方程是不是一元一次方程了吗?以及一个未知数的值是不是一元一次方程的解了吗?
问2:用什么方法能求一元一次方程的解?对这种方法你有什么想说的吗?
问3:你还有什么问题吗?
如果说教育教学工作是“教无定法”,那么是否也可以说“问无定法”,归根结底,数学课堂中的设问,其实就是一切以学生为主体开展有效课堂教学,让学生能迅速、正确地理解问题的指向,充分培养学生的思维能力,激发学生的探究意识。
编辑 鲁翠红
