基于动力系统理论的一类金融混沌系统的定性分析
2017-03-28张光云
张 光 云
(重庆工商大学 数学与统计学院,重庆 400067)
基于动力系统理论的一类金融混沌系统的定性分析
张 光 云
(重庆工商大学 数学与统计学院,重庆 400067)
根据动力系统的基本理论与方法,针对一类三维金融动力系统,研究了该类金融动力系统的平衡点及其附近轨线的性态、解的最终界、全局吸引域、不变集等;最后,给出了相应的计算机仿真.这有助于加深人们对各种金融政策的理解,该混沌系统有望应用于控制工程、图像加密、混沌电路设计等领域中.
混沌系统;稳定性;奇点;计算机仿真;拓扑结构
20世纪以来,非线性系统科学得到了进一步的研究和发展,自从Lorenz系统被发现以来,其他一些混沌系统相继被发现和研究,如Rössler系统,Chua电路系统、Chen系统、Lü系统、超混沌MCK电路系统、广义Lorenz系统、超混沌Rössler系统、超混沌Chen系统等,这些系统的动力学特性,如分岔、控制和同步等也被广泛地研究[1-14].
本文依据动力系统的基本理论与方法对一类金融动力系统的动力学特性进行了研究. 这有助于加深人们对各种金融政策的理解,该混沌系统有望应用于控制工程、图像加密等领域中.
1 数学模型及其主要结果
一个三维金融混沌系统的数学模型为[15]
(1)
其中,变量x,y和z分别代表利率、投资需要和价格指数;a>k>0,b>0,c>0是系统的正参数,分别代表节省成本、单位投资成本和市场需要的弹性数;kx表示平均利润率.当a=0.6,b=0.2,c=0.9,k=0.5时,系统(1)的混沌吸引子见图1.混沌系统(1)各个变量x,y和z随时间演化的图形见图2.

图1 系统(1)的混沌吸引子Fig.1 Chaotic attractor of system (1)
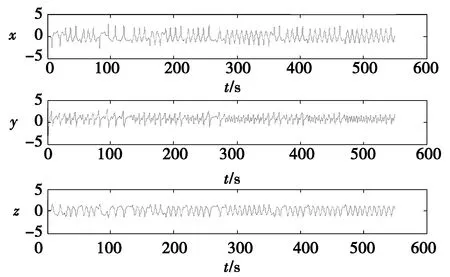
图2 系统(1)的各个状态变量随时间演化图形Fig.2 The diagram of all state variables changing with time
1.1 对称性和不变性
系统(1)具有对称性,即在坐标变换(x,y,z)→(-x,y,-z)下,系统(1)保持不变.y轴为系统(1)的一个不变集,并且从y轴上任何点出发的轨线当t→+∞时都趋于点(0,0,0).
1.2 耗散性和吸引子
记系统(1)的向量场为
F(x,y,
则对于系统(1),有

1.3 奇点及其附近轨线的性态

ii) 当c-b-(a-k)bc≥0时,系统(1)有3个平衡点:


当c-b-(a-k)bc=0,0
1.4 解的最终界
定理1 设X(t)=(x(t),y(t),z(t))为系统(1)的任意一个解,对任意的参数a>k>0,b>0,c>0,令
R2=
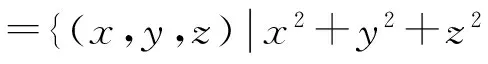
证明 定义Lyapunov函数
V(X)=x2+y2+z2
对此函数沿着系统(1)正半轨线求导数:
2x(z+xy-ax+kx)+2y(1-by-x2)+
2z(-x-xz)=-2(a-k)x2-2by2-2cz2+2y

Γ

由条件极值问题的求法可以得到:

容易证明Δ为系统(1)的一个最终有界集与正向不变集.证毕.
1.5 全局吸引域
定理2 设X(t)=(x(t),y(t),z(t))为系统(1)的任意一个解,则对任意的a>k>0,b>0,c>0,令
V(X)=V(x,y,z)=x2+y2+z2
θ=min(a-k,c,b)>0,
当V(X(t))>L0,V(X(t0))>L0,系统(1)轨线存在下列估计式:
V(X(t))-L0≤(V(X(t0))-L0)e-θ(t-t0)
从而
≤L0}
为系统(1)的一个全局指数吸引集.
证明 定义Lyapunov函数
V(X)=V(x,y,z)=x2+y2+z2
当V(X(t))>L0,V(X(t0))>L0,沿着系统(1)正半轨线求导有:
2x(z+xy-ax+kx)+2y(1-by-x2)+2z(-x-xz)=-2(a-k)x2-2by2-2cz2+2y≤-(a-k)x2-by2-cz2-(a-k)x2-by2-cz2+2y≤
-θx2-θy2-θz2-by2+2y≤


(2)
对不等式(2)两边积分有:
V(X(t))-L0≤(V(X(t0))-L0)e-θ(t-t0)
(3)
令t→+∞,对不等式(3)两边取上极限:

≤L0

2 数值仿真


图3 系统的轨线最终界估计图示Fig.3 The diagram of ultimate bound estimate of the trajectory of the system
3 结 论
基于动力系统的理论与方法,定量和定性地分析了一类金融动力系统的动力学行为,包括奇点及其附近轨线的拓扑类型、吸引子、最终界、全局吸引集、不变集等. 这有助于加深人们对各种金融政策的理解,该混沌系统有望应用于控制工程、图像加密等领域中.
[1] 王兴元.广义M-J集的分形机理[M].大连:大连理工大学出版社,2002
WANG X Y.The Generalized Fractal Mechanism of M-J Set[M].Dalian:Dalian University of Technology Press,2002
[2] 王兴元.混沌系统的同步及在保密通信中的应用[M].北京:科学出版社,2011
WANG X Y.Synchronization of Chaotic Systems and Its Application in Secret Communication[M].Beijing:Science Press,2011
[3] ZHANG F C,MU C L,ZHOU S M,et al.New Results of the Ultimate Bound on the Trajectories of the Family of the Lorenz Systems[J].Discrete and Continuous Dynamical Systems Series B,2015,20(4): 1261-1276
[4] ZHANG F C,MU C L,LIX W.On the Boundness of Some Solutions of the Lü System[J].International Journal of Bifurcation and Chaos,2012,22(1):1-5
[5] ZHANG F C,ZHANG G Y.Further Results on Ultimate Bound on the Trajectories of the Lorenz System[J].Qualitative Theory of Dynamical Systems,2016,15(1): 221-235
[6] LIN D,ZHANG F C,LIU J M.Symbolic Dynamics-based Error Analysis on Chaos Synchronization Via Noisy Channels[J].Physical Review E,2014,90:1-7
[7] CHOWDHURY M S H,HASHIM I.Application of Multistage Homotopy-Perturbation Method for the Solutions of the Chen System[J].Nonlinear Analysis:Real World Applications,2009,10 (1):381-391[8] ELABBASY E M, El-DESSOKY M M.Synchronization of Van Der Pol Oscillator and Chen Chaotic Dynamical System[J].Chaos,Solitons and Fractals,2008,36:1425-1435
[9] WU X F,CHEN G R,CAI J P.Chaos Synchronization of the Master-Slave Generalized Lorenz Systems Via Linear State Error Feedback Control[J].Physica D,2007,229:52-80[10] WU X Y, GUAN Z H,WU Z P,et al.Chaos Synchronization Between Chen System and Genesio System[J].Physics Letters A,2007,364(6):484-487
[11] STARKOV K E,STARKOV J K K.Localization of Periodic Orbits of the RöSsler System under Variation of Its Parameters[J].Chaos,Solitons and Fractals,2007,33(5):1445-1449
[12] PARK J H,LEE S M,KWON O M.Dynamic Controller Design for Exponential Synchronization of Chen Chaotic System[J].Physics Letters A,2007,367(4-5):271-275
[13] HEGAZI A,AGIZA H N,EL-DESSOKY M M.Controlling Chaotic Behaviour for Spin Generator and Rossler Dynamical Systems with Feedback Control[J].Chaos,Solitons and Fractals,2001,12:631-658
[14] HEGAZI A S,AGIZA H N,El-DESSOKY M M.Synchronization and Adaptive Synchronization of Nuclear Spin Generator System[J].Chaos,Solitons and Fractals,2001,12(6):1091-1099
[15] CAI G L,YU H J,LI Y X. Localization of Compact Invariant Sets of a New Nonlinear Finance Chaotic System[J].Nonlinear Dynamics,2012,69:2269-2275
责任编辑:李翠薇
Qualitative Analysis of a Class of Financial Chaotic System Based on Dynamical System Theory
ZHANG Guang-yun
(School of Mathematics and Statistics, Chongqing Technology and Business University, Chongqing 400067, China)
Based on the basic theory and method of dynamical system, according to a class of three-dimensional financial dynamic systems, this paper studies the equilibrium point of this class of financial dynamic system, its nearby trajectory property, the final boundedness of the solution, global attractive sets, invariant set and so on, and ultimately gives corresponding computer simulation. This research is conducive to deepening the understanding of all kinds of financial policies, and this chaotic system is expected to be applied to control engineering, image encryption, chaotic circuit design and so on.
chaotic system; stability; singular point; computer simulation; topological structure
2016-09-14;
2016-10-23.
张光云( 1983-),女,山东临沂人,助教,硕士,从事外国语言学及应用语言学、常微分方程研究.
10.16055/j.issn.1672-058X.2017.0002.009
O241.84;O29;O242.1
A
1672-058X(2017)02-0037-04
