人民币汇率厚尾特征及VAR估计*
2017-03-28吴慧慧
吴 慧 慧
(岭南师范学院 数学与计算科学学院,广东 湛江 524048)
人民币汇率厚尾特征及VAR估计*
吴 慧 慧
(岭南师范学院 数学与计算科学学院,广东 湛江 524048)
针对人民币汇率收益率序列的厚尾性特征,基于EGARCH模型得到标准化的收益率序列,建立GPD模型对标准化收益率序列的尾部进行拟合,并得到相应的VAR估计值;结论证明:人民币收益率序列存在双厚尾特征,故对于人民币汇率的投资者,无论做多头还是空头,都面临着较大的自身风险和交易对手风险。
人民币汇率收益率;EGARCH模型;GPD模型;风险价值;失败率检验
汇率改革之后,人民币汇率的波动幅度逐渐增大,波动幅度的增大就意味着人们投资外汇市场的风险也在变大。VAR方法是当今国际上比较通用和流行的风险度量方法,指在一定的置信水平下,在市场处于正常的波动条件下,某一资产或资产组合在未来一段时间内可能发生的最大损失。
在实际的风险管理中,人们往往会对金融资产的大起大落比较关心,并且大量实证分析证明基于传统的方差-协方差方法、历史模拟法、蒙特卡洛模拟方法等估计的VAR值比较低效[1]。为了更加准确的估计VAR值,极值理论被用于风险度量的研究中。基于极值方法度量金融资产风险,国内外学者进行了大量的研究[2-5]。一般来说,极值理论对风险的度量主要分为两大模型:块最大值模型(BMM模型)和广义帕累托模型(GPD模型),前者主要是针对组最大值建模,后者是针对观测值中超过某一门限值(threshold)的数据建模。对于金融机构和金融投资者而言,他们更关心的是观测数据超过某一门限值之后金融时序的变化,因此,在实践中,GPD模型应用更为广泛。本文拟使用GPD模型估计人民币汇率收益率分布尾指数,在此基础上得到VAR估计。
1 模型方法介绍
大量研究表明,金融资产的收益率过程一般都存在波动集聚性、条件方差时变性、长记忆性、非对称性等非线性特征,这违背了极值理论应用的前提:样本来自于独立同分布的总体。因此,在使用极值理论估计VAR之前,此处使用GARCH类模型对金融资产的收益率序列进行过滤,得到标准化的残差序列,即标准化的收益率序列。对于波动模型的选取,论文选用既放松了对GARCH模型参数非负性约束,又可以反映出杠杆效应的指数GARCH(EGARCH)[6]。相对于其他分布,正态分布具有薄尾的特征,为了不影响原收益率序列的厚尾性,方差方程中条件分布设定为正态分布。EGARCH(1,1)模型方差方程的具体形式设定为

(1)
其中,εt=ztσt,zt~N(0,1),{zt}即为标准化的残差序列,即标准化收益率序列。
1.1GPD模型
广义Pareto分布(GPD)的定义如下:
(2)
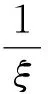
对金融资产的投资者而言,他们更关注的是超过某个门限值u(threshold)后的金融时序变化情况。
设X1,X2,…,Xn是独立分布的随机变量,具有相同的分布函数F(x),对于门限值u,超出量Yi=Xi-u的分布为

(3)
超过门限值u的尾部分布可以表示为
1-F(x)=(1-F(u))(1-Fu(y))
(4)
根据历史模拟法,若样本容量为n,门限值u充分大,Nu表示样本中超过门限值u的样本数量,则
(5)
Pickands研究[9]表明,若门限值u充分大,
Fu(y)~Gξ,β(u)(y)
(6)
则对于充分大u,超过门限值u的尾部分布可近似表示为
(7)

1.2 门限值u的选取
关于门限值u的选择非常关键,它是正确估计参数ξ和β以及得到准确的VAR值的前提。门限值过小,极限定理不成立,得到的参数估计是有偏的;门限值过大,则可以分析的数据减少导致估计的方差增加。在实证分析中一般根据QQ散点图、样本均值超过数(MME)散点图和Hill散点图三者结合起来进行确定。
相对于正态分布的薄尾特征,指数分布具有中等厚度的尾部,故QQ散点图一般与指数分布进行比较。关于QQ散点图的原理可参考文献[10]。
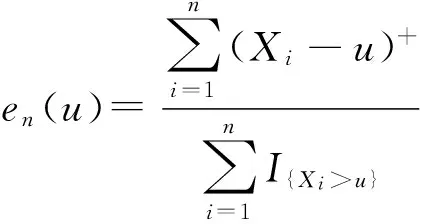
若MME散点图近似为门限u的增函数,则初步估计为厚尾分布;反之,若MME表现近似为水平或向下的直线,则初步估计为薄尾分布。
Hill散点图是根据ξ的Hill估计量得到的:
(8)

1.3 尾指数估计检验

1.4VAR估计
VAR(Value at risk)即风险中的价值,是指在正常的市场条件下和给定的置信度内,某一金融资产或资产组合在未来特定持有期内的最大可能损失。对于给定的显著性水平α(0<α<1),假设{zt}为某一金融资产或金融资产组合的收益率,zt为t时刻的收益率,则定义风险值VARα(t)为满足:
P(zt> VARα(t)) =α
(9)
的(1-α)上分位数。由于显著性水平α的取值较小,一般取0.05,0.01,0.001,因此风险值VARα反映了金融市场中资金流的异常流动以及金融资产价格的异常变动和潜在损失的可能性大小[10]。则由式(7)可知,VARα的估计为
(10)
2 实证研究
2.1 样本数据的选取及简单分析
2005年7月21日,我国人民币汇率形成机制由盯住美元的固定汇率制改为以市场供求为基础的、顶住一揽子货币的浮动汇率制度。本文选取2005-07-22—2015-12-30间每个外汇交易日美元兑人民币中间牌价作为研究对象,数据来源于国家外汇管理局。
收益率的计算采用对数收益率的形式,汇率中间价序列{Pt}取对数之后进行一阶差分得到序列{Rt}:
Rt= 100×(lnPt- lnPt - 1)
(11)
对人民币汇率收益率的统计分析,采用的统计量为均值、最大值、最小值、标准差、偏度系数、峰度系数、Jarque-Bera统计量,结果如表1所示,图1为收益率序列的时序图,表2为收益率序列的BDS独立性检验结果。

表1 收益率R的基本统计特征
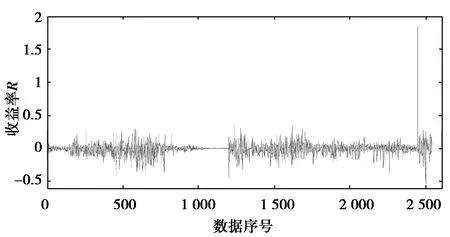
图1 收益率R的时序图Fig.1 The timing diagram of the rate return R
表2 收益率序列的BDS独立性检验结果
Table 2 The BDS independence test results of the rate returnR
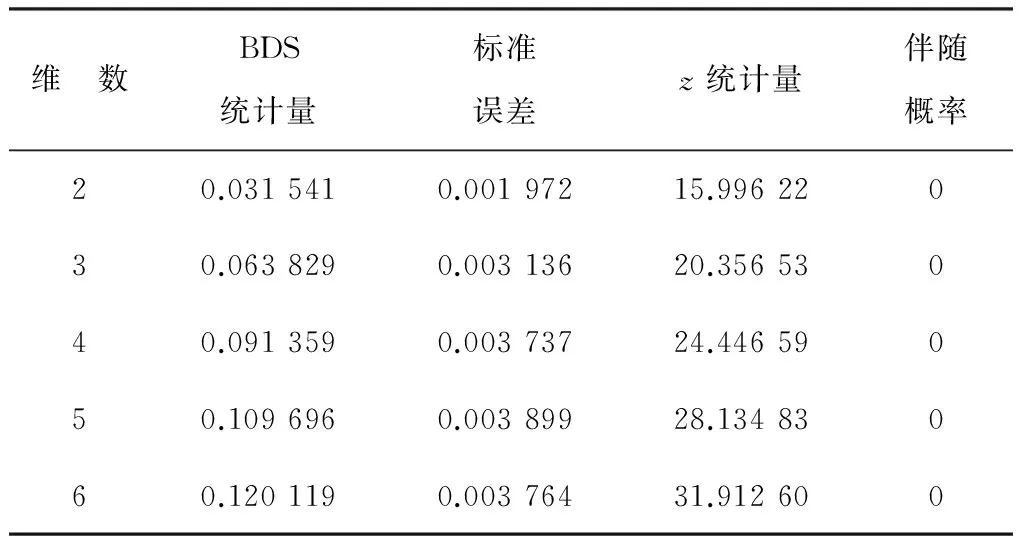
维 数BDS统计量标准误差z统计量伴随概率20.0315410.00197215.99622030.0638290.00313620.35653040.0913590.00373724.44659050.1096960.00389928.13483060.1201190.00376431.912600
由表1可知,人民币汇率收益率偏度系数为4.727 2>0,因此序列的分布不是围绕均值对称分布的,存在一定的右偏性;峰度为90.889 9,显著的大于正态分布的峰度3,存在超额峰度,序列存在厚尾特征;J-B统计量相应的p值为0,说明序列显著拒绝正态分布的原假设。由表2可知,收益率序列在5%的显著性水平下其BDS统计量都显著不为0,说明了序列是不独立的。峰度这一统计量是基于序列是独立且服从正态分布的假设下给出的结果,单纯根据峰度的取值去衡量收益率序列的厚尾特征,有可能会高估厚尾风险。
由图1可知,收益率R的波动存在着明显的集聚特征:汇率收益率波动性从2006年开始逐渐增加,这是我国汇率制度改为浮动汇率制度的结果。到2008年10月份汇率的波动幅度大幅上升,这可能是由于全球金融危机的爆发引起的。2009年到2010年的6月份,汇率的波动幅度相对比较小,但是其后,汇率的波动一直维持着比较大的幅度。
2.2 样本数据的处理
由数据分析可知收益率序列并不是相互独立的,而是存在着波动集聚性、长记忆性和非对称性等非线性特征,这违背了极值理论要求序列之间是相互独立的前提。论文使用EGARCH(1,1)模型剔除收益率序列的非线性特征得到标准化的收益率序列。
由于GARCH类模型只适用于平稳性数据建模,故首先对收益率序列进行ADF检验,由收益率序列的均值为-0.008 8,故假定收益率序列在0附近波动,ADF统计回归方程中不含常数项和时间趋势项,得到ADF统计量的值为-39.361 8,相应的p值为0,故认为收益率序列是平稳的。因此可以使用EGARCH模型对序列进行拟合。
通过软件Eviews 6.0可得方差方程参数估计的结果如表3:
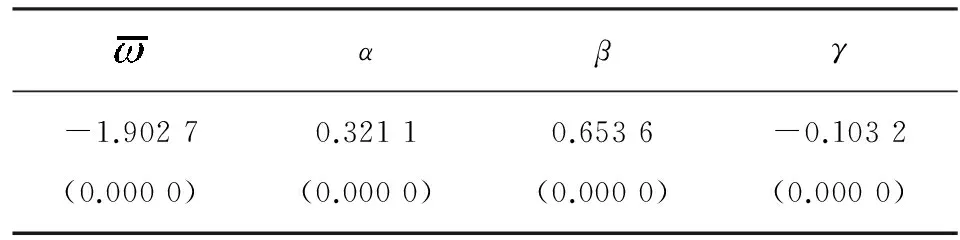
表3 EGARCH模型估计结果
注:括号内为相应参数估计值的p值。
根据模型估计的结果可以得到汇率收益率的标准化残差,即标准化的收益率序列{zt}。
2.3GPD模型参数估计及诊断
采用GPD模型拟合标准化收益率的尾部,首先确定门限值u。

图2 确定上尾指数门限值的相关图Fig.2 The correlation diagrams of the upper tail index threshold
由图2(a)可知,序列{zt}的上尾相对于指数分布具有显著的厚尾特征;由图2(b)可知,在门限值1.5~1.75附近,曲线近似为向上倾斜的直线,进一步通过2(c)发现,在门限值1.715附近,形状参数表现得相对稳定,故上尾指数的门限值取为1.715。

图3 确定下尾指数门限值的相关图Fig.3 The correlation diagrams of the lower tail index threshold
由图3(a)可知,序列{zt}的下尾相对于指数分布也具有显著的厚尾特征;由图3(b)可知,在门限值1.8~1.9附近,曲线近似为向上倾斜的直线,进一步通过3(c)发现,在门限值1.842附近;形状参数表现得相对稳定,故下尾指数的门限值取为1.842。
门限值确定之后就可以对GPD分布进行参数估计,表4为上尾和下尾参数估计的结果:
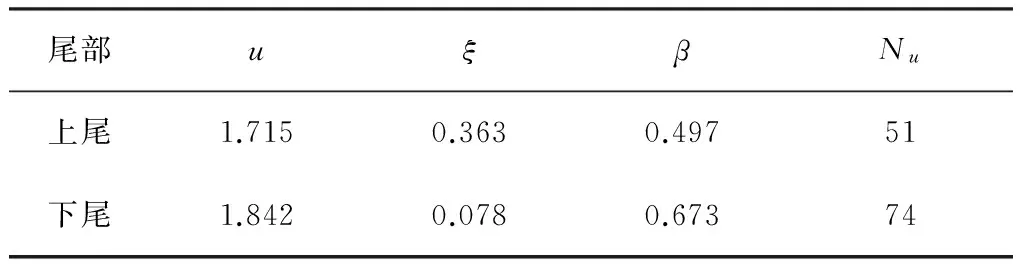
表4 参数估计的结果
从估计结果上可以看出,序列{zt}的上尾和下尾的形状参数ξ都是显著大于0的,进一步说明了序列{zt}的上尾和下尾都存在厚尾性特征。
关于参数估计的诊断,论文采用截断分布拟合、尾分布拟合、残差拟合来完成。
图4和图5分别是时序上尾和下尾模型诊断的检验结果,由图4,5可知参数估计的结果总体来说比较理想且下尾参数估计的结果相对更好。

图5 下尾模型诊断结果Fig.5 The diagnosis results of lower tail model
2.4VAR估计与有效性诊断
不同置信水平下的VAR估计值及有效性检验的结果如表5所示:

表5 VAR估计值及有效性检验
从表4可以看出,整体上来说使用GPD模型预测人民币汇率收益率的风险值是比较理想的;下尾对VAR值的预测较上尾更准确;上尾实际失败个数总是小于理论失败个数,可能存在着低估极端风险的可能性;在较低的置信水平下对VAR值的预测不如较高置信水平下的准确度高。
3 结 论
随着人民币汇率波动幅度的增大,对外汇风险的度量成为外汇投资者比较关注的问题,过去人们常常用正态分布作为参考模型,使用其方差来度量风险,虽然操作简单,但是比较容易低估风险。
本文根据人民币汇率收益率的数据特征,基于极值理论GPD模型对人民币汇率标准化收益率序列建模,得出其存在双厚尾的风险,这就说明在剔除了汇率收益率过程中的波动集聚性和杠杆效应等非线性特征之后,人民币汇率标准化收益率出现大幅上涨或大幅下跌的可能性均高于基于正态分布的预测,对于人民币汇率的投资者,无论是做多头还是空头都面临着较大自身风险和交易对手风险。
在GPD模型的基础上,得到上尾和下尾的VAR估计值,并检验了其有效性。在较高的置信水平下,结果比较理想,这在实践中可以保证准备资金的充分利用,避免无效率的经济资本的配置,从而可以为金融管理者和外汇投资者提供风险度量的方法借鉴。
[1] 欧阳资生,龚曙明.广义帕累托分布模型:风险管理工具[J].财经理论与实践,2005,26(137):88-92
OU Y Z S,GONG S M.GPD Model as a Risk Management Tool[J].The Theory and Practice of Finance and Economics,2005,26 (137):88-92
[2] 王宗润,吴伟韬,陈超,等.人民币汇率风险的测度[J].统计与决策,2009,283(7):118-120
WANG Z R,WU W T,CHEN C,et al.Measurement of RMB Exchange Rate Risk[J].Statistics and Decision,2009,283 (7):118-120
[3] 高莹,周鑫,金秀.GARCH-EVT模型在动态VAR中的应用[J].东北大学学报(自然科学版),2008,29(4):601-604
GAO Y,ZHOU X,JIN X.Application of GARCH-EVT Model in Dynamic VAR[J].Journal of Northeastern University (Natural Science Edition),2008,29(4):601-604
[4] 高岳,张翼.深成指GPD分布尾部拟合与VAR-ES风险度量[J].统计与决策,2012,(18):157-159
GAO Y,ZHANG Y.The GPD Tail Distribution Fitting and VAR-ES Risk Measurement of Shenzhen Component Index[J].Statistics and Decision,2012(18):157-159
[5] SELENA T,MILICABULAJIC F,TAMARA V.Empirical Comparison of Conventional Methods and Extreme Value Theory Approach in Value-At-Risk Assessment[J].Business Management,2011,5(33):12810-12818
[6] NELSON D B. Conditional Heteroskedasticity in Asset Returns:A New Approach[J].Econometrica,1991,59(2):35-42
[7] 桂文林,韩兆洲,潘庆年.POT模型中GPD“厚尾”性及金融风险测度[J].数量经济技术经济研究,2010(1):107-118
GUI W L,HAN Z Z,PAN Q N.Tail Thickness of GDP in POT Model and Finance Risk Measurement[J].The Journal of Quantitative & Technical Economics,2010(1):107-118
[8] GENCAY R,SELCUK F.EVIM:A Soft Package for Extreme Value Analysis in MATLAB[J].Studies in Nonlinear Dynamics and Econometrics,2001,5(3):213-239
[9] PICKANDS J.Statistical Inference Using Extreme Order Statistics[J].The Annals of Statistics,1975(3):119-131
[10] 彭作祥.金融时间序列建模分析[M].成都:西南财经大学出版社,2006
PENG Z X.Modeling and Analysis of Financial Time Series[M].Chengdu:Southwestern University of Finance and Economics Press,2006
责任编辑:李翠薇
Heavy Tail Characteristics and VAR Estimation of RMB Exchange Rate
WU Hui-hui
(School of Mathematics and Computer Science, Lingnan Normal University, Guangdong Zhanjiang 524048, China)
The paper aimed at the heavy tailed characteristic of the RMB exchange rate sequence,based on the EGARCH model to get the standard rate of return sequence, established a GPD model to fit the tail of the normalized yield sequence, and got the corresponding estimation of VAR. The results showed that the sequence of RMB returns had the characteristic of bilateral heavy tail. Thus, for the investors of RMB exchange rate, they would face a greater risk of their own and counterparty whether to do long or short.
RMB exchange rate return; EARCH model; GPD model; value-at-risk; test of failure rate
2016-09-02;
2016-10-22.
岭南师范学院校级自然科学青年项目(QL1409).
吴慧慧(1987-),女,山东菏泽人,讲师,硕士研究生,从事金融数学与金融工程研究.
10.16055/j.issn.1672-058X.2017.0002.010
F822;O211
A
1672-058X(2017)02-0041-07
