线段和的最小值问题再探究

陕西师范大学附属中学(710056) 曹艳

线段和的最小值问题再探究

陕西师范大学附属中学(710056) 曹艳

初中阶段的线段最值问题都是以“两点之间,线段最短”为理论依据的.同时实际运用过程中也用到“三角形两边之和大于第三边”,“三角形两边之差小于第三边”,有时候还会结合“垂线段最短”的结论.无论是两条线段和还是三条线段和的最小值问题,最终都要转换为两点之间线段最短问题.

一、利用轴对称变换求解线段和最小值

基本模型:

1.“一定一动”问题:根据“直线外一点与直线上各点连接的所有线段中,垂线段最短”,可知已知点到已知线段的最小值为对应垂线段长度.

2.“两定一动”问题:教材中的“牛奶站”问题,“将军饮马”问题等,都是根据轴对称性,结合“两点之间,线段最短”来求线段和的最小值,可以归结为“两定一动”问题.

3.“一定两动”问题:

例1.如图1,点P位于l1和l2之间,M、N分别在l1和l2上,试确定 M、N 位置使得PM+MN+PN最小.

图1

分析:这个问题需要作点P关于l1和l2的对称点,PM+MN+PN=P′M+ MN+P′′N≥P′P′′,即点P′、M、N、P′′四点共线时PM+MN+PN最小.这个模型还可以放至菱形或者等腰三角形中.

例2.如图2,点P位于l1和l2之间,M、N分别在l1和l2上.试确定M、N位置使得PM+MN最小.

图2

分析:此题只需作点 P关于 l1的对称点 P′,有PM+MN=P′M+MN≥P′N,即当P′、M、N三点共线时PM+MN最小,为P′N.点N在l2上运动,由垂线段最短可知,当P′N⊥l2时P′N最小,此时PM+MN最小.

4.“两定两动”问题:

例3.如图3,P、Q为定点,M为l1上一动点,N为l2上一动点,求PQ+PM+MN+NQ的最小值.

图3

分析:作点P关于l1的对称点P′,点Q关于l2的对称点Q′,则PQ+PM+MN+NQ=PQ+P′M+MN+NQ′≥PQ+P′Q′,当P′、M、N、Q′四点共线时PQ+PM+MN+ NQ最小,为PQ+P′Q′.

有的则需要借助平移来转化为第(2)种情形.举例说明:

例4.如图4,P、Q两点分别位于河流两侧,河宽为a米,l1//l2.需要在河上修建一座桥,使得桥MN垂直于岸边l1,试问MN建在何处使得PM+MN+QN最小.

图4

分析:将点P沿垂直于l1的方向平移a米,易证四边形PP′NM为平行四边形.因此PM+MN+QN= P′N+MN+QN ≥a+P′Q,即P′、N、Q共线时PM+MN+QN最小.

例5.如图5,点A、B位于直线l的同侧,定长为a的线段MN在l上滑动,请问MN滑动到何处时AM+MN+BN最小.

图5

分析:将点A沿平行于l的方向平移a至A′点,易证四边形AMNA′为平行四边形.作点A′关于直线l的对称点A′′.因此AM+MN+BN= A′N+MN+BN=A′′N+MN+BN≥a+A′′B,即A′′、N、B三点共线时AM+MN+BN最小.

图6

例6.如图6,在边长为10的菱形ABCD中,对角线BD=16,E为AB的中点,P、Q是BD上的动点,且始终保持PQ=2,则四边形AEPQ的周长的最小值为多少?

分析:根据菱形的对称性可知点A关于BD的对称点为点C,则AQ=CQ.将点E沿BD方向平移2个单位,则四边形EPQE′为平行四边形,故EP=E′Q.则四边形AEPQ的周长为AE+EP+PQ+AQ= AE+E′Q+PQ+CQ=5+2+E′Q+CQ≥7+CE′,易求得因此四边形AEPQ的周长为

5.“三动”问题:

例7.如图7,四边形ABCD为菱形,已知M、N分别是边BC、CD上的动点,P是对角线BD上一点,则PM+PN的最小值是多少?

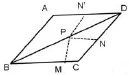
图7

分析:由菱形对称性可知点N关于BD的对称点N′在AD上,则PM+PN=PM+PN′≥MN′,即当M、P、N′三点共线时PM+PN最小,为MN′.而只有MN′⊥BC时MN′最小,因此PM+PN的最小值即为BC和AD之间的距离.

二、利用旋转变换求解线段和最小值

例 8.如图 8,四边形ABCD是边长为2的正方形,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN,AM,CM,则当M在BD上运动时,(AM+BM+CM)2的最小值为多少?

图8

分析:若求(AM+BM+CM)2的最小值,即求AM+BM+CM的最小值.在此需要将三条线段转化,利用两点之间线段最短来解决.

解析:先转化AM.∵△ABE为等边三角形,∴BA= BE.∵∠ABM+∠ABN=∠EBN+∠ABN=60°,∴∠ABM=∠EBN.又∵BM=BN,∴△ABM～=△EBN(SAS),∴AM=EN.再转化BM,连接MN.∵BM=BN,∠MBN=60°,∴△BMN为等边三角形,BM=MN.因此AM+BM+CM=EN+MN+CM,当E、N、M、C四点共线的时候AM+BM+CM最短,其最小值为EC的长度.

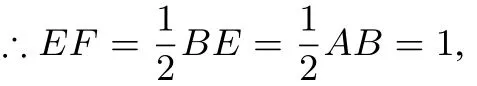
例9.如图10,已知正方形ABCD内一动点P到A、B、C三点的距离之和最小值为,则正方形的边长是______.

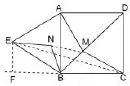
图9

分析:该题目的已知条件与所求结论恰和上例相反,我们可以用类似的方法来求解.

解析一:如图 11,不妨在正方形ABCD外部以AB为边作等边△ABE,同时将线段BP绕点B逆时针旋转60°得到BN,连接EN,NP.

图10

仿照上例我们可以证明将线段AP转化为EN,将BP转化为NP,则有AP+BP+CP= EN+NP+CP,当E、N、P、C四点共线时AP+BP+CP最小,为,即.

图11

当然我们是受到例8的启发,运用相似模型解决了例9的问题.如果我们直接运用旋转的特性也可以按照下面的思路进行求解.

解析二:不妨以点A为旋转中心,将△ABP绕点A顺时针旋转60°得到△AEN(用紧密虚线显示),连接BE,BN,NP,如图12.

图12

容易证明△APN为等边三角形,∴AP=NP.又BP=EN,∴AP+BP+CP=NP+EN+CP,当E、 N、P、C四点共线时AP+BP+CP最小,为,即.容易证明△AEB为等边三角形,其余同上.

我们在解决这个三条线段和最小的问题时,将其转化为两点之间线段最短的问题.同时条件稍作改变之后我们还可以用类似方法去套这个模型.

数学题目千变万化,稍作改变就是一道全新的题目,所以提示我们在解题过程中注意触类旁通,发散思维,这样往往会有意想不到的效果.而其实这道题目是费马点的变形.下面我们看看什么是费马点:

费马点,就是到三角形的三个顶点的距离之和最小的点.所谓费马点结论是这样的:对于一个各角不超过120°的三角形,费马点是对各边的张角都是120°的点;对于有一个角超过120°的三角形,费马点就是这个内角的顶点(这里不再赘述证明过程).解决费马问题的方法主要就是运用旋转变换.近几年,费马问题逐渐走进了中考的阵地,而这个有趣的数学问题也有很多的变形,本文中的例题恰恰如此,不过万变不离其宗,解决方法依然是旋转变换.

三、启示

初中阶段学习的五种变换:平移变换、轴对称变换、中心对称变换、旋转变换以及位似变换,其中前四种是全等变换,第五种是相似变换.在求解线段和最小值的问题中,我们常用的就是平移变换、轴对称变换和旋转变换.不论是哪一种模型,都需要准确找出变化过程中的不变量,如轴对称变化中的对应线段、旋转变换中的对应线段等等,以此作为解题突破口.此类问题可以在等腰三角形、等腰梯形、长方形、菱形、正方形、正多边形、圆等基本图形中出现,还可以与二次函数抛物线相结合,因此教学过程中,可依据学生情况适时引导,培养学生在解题过程中的观察力,逐步体会问题实质.