初中数学解题策略之周密谋划防遗漏

林学明

摘要：漏解是导致学生丢失分数的主要原因之一，在解答初中数学题目时，教师要注意引导学生保持思维的严谨性，周密谋划，运用有效的解题策略，从而防止漏解，提高考试得分。本文阐述了初中数学解题的三种策略，旨在减少学生不必要的丢分。

关键词：初中数学 解题策略 周密谋划

数学学习离不开解题，解题是巩固知识、深化理解、拓宽思路、提升能力的重要途径。合理运用解题策略，有助于提高学生的解题速度和效率。然而，在解答数学问题时，学生由于思考不全面，做题经验不足，没有完整地写出解题过程，以至于解题时出现各种遗漏，导致不必要的丢分。因此，在初中数学教学中，教师要注意有效渗透解题策略和思想方法，引导学生周密谋划，巧妙解题，从而培养学生良好的解题思维，提高学生的解题正确率。

一、分类讨论，防止遗漏

初中数学考试中有些题目会出现指代不明的情况，如果学生思维不严密，就可能出现遗漏。如在有些关于等腰三角形的题目中，给定的边没有指明是底边，还是腰，学生就要根据不同情况进行分析；再如解不等式（k-1）x﹥k2-1时，学生若不加以区分k-1的取值范围，就容易出现遗漏，得出错解。实际上，这道题目的答案既可能是k-1﹥0，又可能是k-1﹤0，还可能是k-1=0。取值范围不同，答案就有所不同。因此，若要防止遗漏，教师必须指导学生开展合理的分类讨论。

首先，教师要引导学生认真阅读题目，明确分类的对象与标准，有效区分与作答。如“直线”“射线”“线段”这三者是有差别的，不可均视为“线段”进行求解；其次，教师要引导学生多方位思考可能出现的不同情况，做到完整答题。

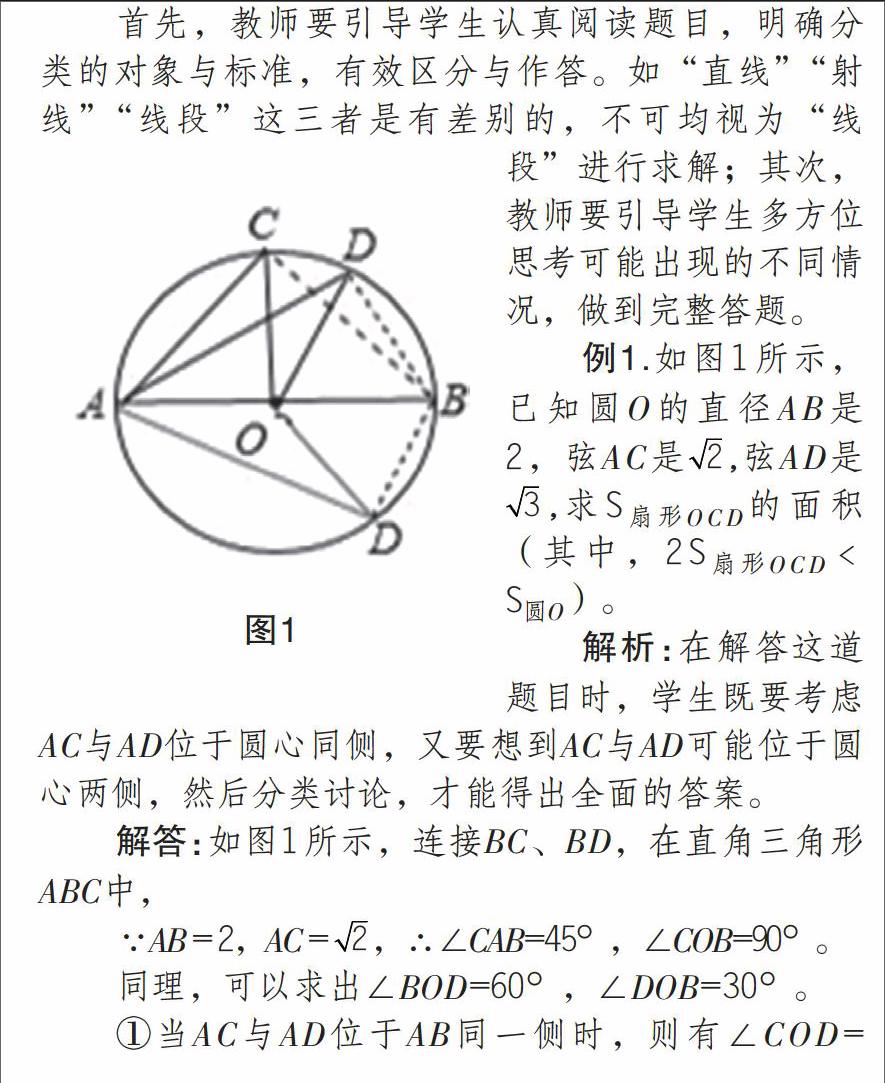
例1.如图1所示，已知圆O的直径AB是2，弦AC是，弦AD是，求S扇形OCD的面积（其中，2S扇形OCD﹤S圓O）。

解析：在解答这道题目时，学生既要考虑AC与AD位于圆心同侧，又要想到AC与AD可能位于圆心两侧，然后分类讨论，才能得出全面的答案。

解答：如图1所示，连接BC、BD，在直角三角形ABC中，

∵AB=2，AC=，∴∠CAB=45°，∠COB=90°。

同理，可以求出∠BOD=60°，∠DOB=30°。

①当AC与AD位于AB同一侧时，则有∠COD=∠COB-∠BOD =90°-60°=30°。因此，可以得出S扇形OCD=。

②当AC与AD分别位于AB两侧时，同①可以得出∠COD=150°，

∴∠S扇形OCD=。

综上所述，S扇形OCD应该是或。

二、抓住特殊性，严防漏解

在解答数学题目时，不少学生会因为对数学概念识记不牢，没有进行全面思考，导致漏解；或者因为对所学知识的理解不深刻，没有注意到题目中包含的隐含条件，导致答案不完整；或者是忽视了问题中一些特殊情况，从而出现漏解。比如在解答一元二次方程时，有的学生没有注意到题目中隐含的限制条件，而出现遗漏或错解。

例2.关于x的方程k2x2+（2k-1）x+1=0存在两个不相等的实数根，求k的取值范围。

解析：面对此题，有的学生会直接根据△=b2-4ac=（2k-1）2-4k2﹥0，仅求出k﹤ ，而没有注意到已知条件所给的关键词——方程有两个不相等的实数根。也就是说该方程是一元二次方程，故二次项系数k2≠0，即k≠0。因此，正确答案应该是k﹤且k≠0。

可见，在解答初中数学题目时，为了避免漏解，学生要深刻理解数学概念，抓住数学知识的特殊性（规定条件），做到周密谋划，准确答题。

三、打破思维定势，避免漏解

在分析数学问题时，有的学生受思维定势影响，运用传统解题经验，常常先入为主，对题中所给的条件思考不周全，没有依据问题特点进行灵活分析，从而出现漏解。如Rt△的两条边长分别是6与8，求该三角形的外接圆半径。在解答该题目时，有的学生受勾股定理的勾股数6，8，10的影响，将6与8直接视为直角边，而出现漏解，其实8还可能是斜边。

总而言之，学习有法，但无定法，贵在得法。在解答初中数学题目时，教师应引导学生周密谋划，全面分析数学概念的条件，注意问题的特殊性，善于合理开展分类讨论，打破思维定势的不利影响，按序排查，考虑到满足条件的不同情况，从而防止漏解，减少答题时不必要的失分。

（作者单位：广东省中山市小榄镇第一中学）