浅谈初中数学繁杂运算

林庆龙

摘 要：数学中考什么样的題目属于繁杂运算？知识点学生熟悉，着重考查学生双基的，需要较大运算量的题目是首选。基于这个考虑，从以下几方面进行突破：多动笔，记忆模型；训练好数学双基；知道繁杂的题目都可以分解；克服畏惧心理；培养解题兴趣。

关键词：中考数学；繁杂运算；原因；解决

数学中考经常碰到一类包含繁杂运算的题目。在我看来，这部分题目考查的知识点指向明确，学生易于掌握，它着重考查的还是学生的双基（基础知识和基本技能），但却带有学生较为畏惧的繁杂运算（如根号或参数等），在命题过程中，假如把根号或参数等去掉，那么题目将失去它的魅力，难以成为试卷中的压轴题。

繁杂运算在初中大致有一元二次方程的整理与求解、多边形的面积计算特别是四边形的面积割补问题、函数的相关计算（如求交点、配方法求抛物线的顶点坐标），这些知识点基本且是必须掌握的内容，按理说不难，就是因为繁杂运算。

繁杂运算向来都是学生在考试中最怕碰到的，碰到之后又最易失分甚至导致整个考试一塌糊涂。它产生的主要原因首先是学生平时动笔较少，遇到此类题时懒于参与，认为过程简单不必一直重复，只要考试时认真就行，忽略了基本解题技能的训练，没有真正动手，没真正体验命题者设置的难度；其次是双基较为薄弱，基础知识没过关，基本的解题技能没有得到落实；第三，学生的应试心理存在缺陷，在体验到容易题和中档题的喜悦之后，没有做好迎接繁杂运算的心理准备，导致一碰上就慌张，其实每一份中考试卷都会有繁杂的运算；第四，由于运算不过关、不熟练，命题者的意图是用三分钟完成的运算学生却用了一二十分钟，导致考试时间紧张；第五，学生的韧性差，曙光来临的一刻却放弃了。以下是两道泉州市中考压轴题，明显有此感觉。

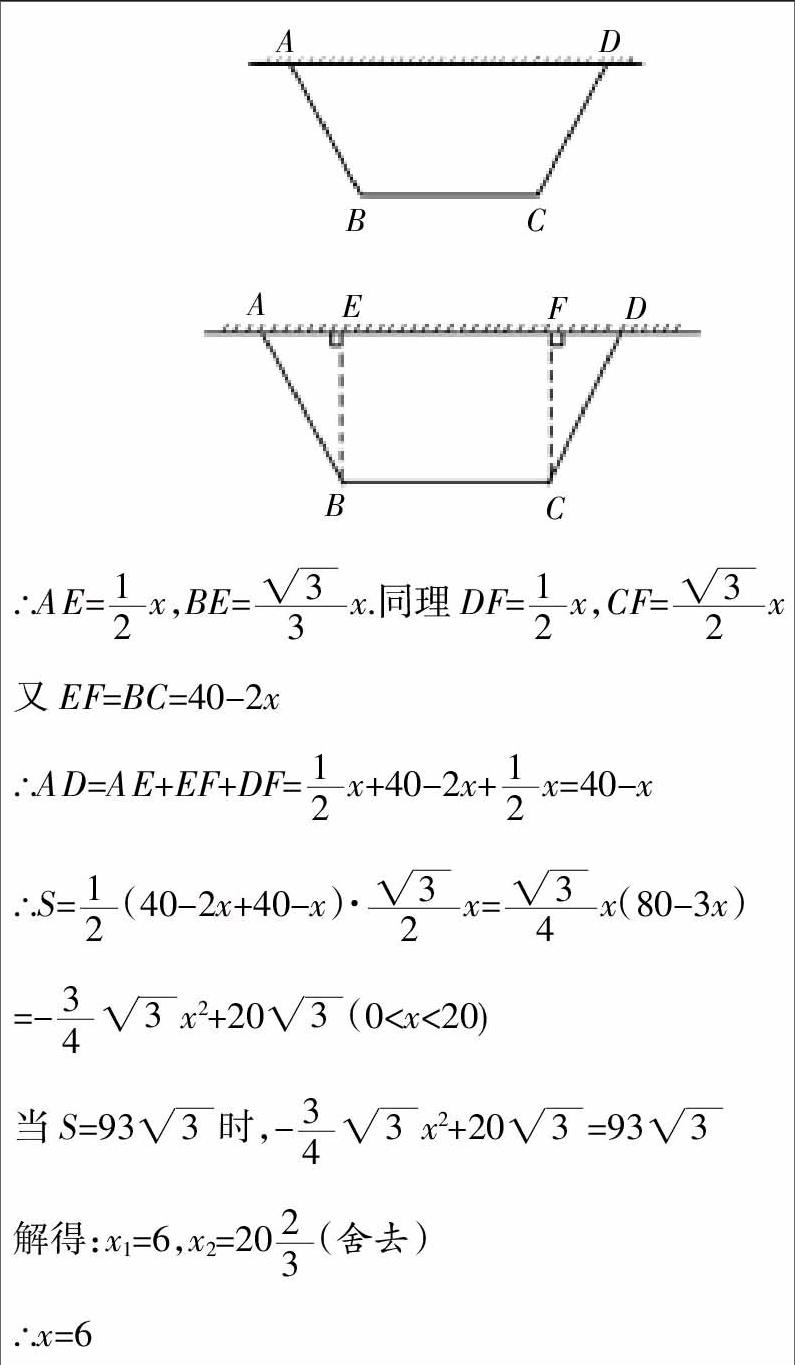
例.（2009年福建省泉州市初中毕业、升学考试27题）（13分）如图，等腰梯形花圃ABCD的底边AD靠墙，另三边用长为40米的铁栏杆围成，设该花圃的腰AB长为x米.

（1）请求出底边BC的长（用含x的代数式表示）；

（2）若∠BAD=60°，该花圃的面积为S米2：

本题的平均得分只有3.9分，明显偏少，分析其难度值0.30，貌似难度偏大，但认真分析题目并不难，指向知识点明确，第（2）①小题考查的知识点是梯形的面积结合解一元二次方程，简单的数形结合。梯形的面积等于（上底+下底）×高÷2，只要能分别表示上底、下底、高就行，而本题的这三个量都不难表示，一元二次方程的解法又是学生必须熟练掌握的知识，按说难不倒学生，但事实恰恰相反，究其原因就是在第（2）①小题中运算繁杂，许多学生不会解带根号的方程，学生认为带根式运算复杂，不懂得将方程两边同除以根式后，再利用计算器求得一元二次方程的解，导致考试中学生花费大量的时间却没有相应的回报，造成心里紧张和时间紧张。

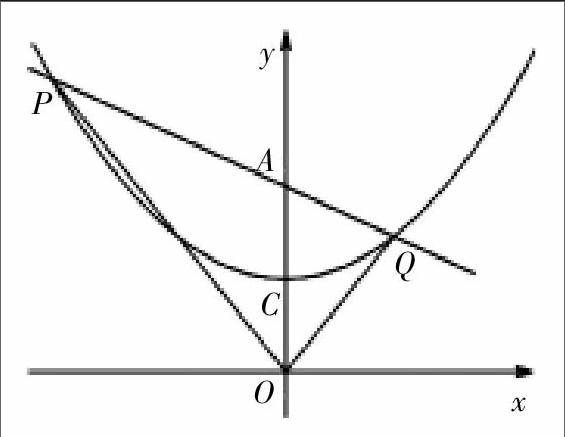
又如：（2012年福建省泉州市初中毕业、升学考试26）（14分）如图，O为坐标原点，直线l绕其上点A（0，2）旋转，与经过点C（0，1）的二次函数y=x2+h的图象交于不同的两点P、Q.

（1）求h的值；

（2）通过操作、观察，算出POQ面积的最小值（不必说理）；

（3）过点P、C作直线，与x轴交于点B，试问：在直线l旋转过程中，四边形AOBQ是否为梯形？若是，请说明理由；若不是，请指出四边形的形状.

在（3）小题的解答中，当l与x轴平行时，四边形AOBQ是正方形，一般没问题。但当l与x轴不平行时，学生就难办，如果认真分析，解决这个问题也是数学的基础知识和基本技能。

当l与x轴不平行时，设P点坐标（a，b），C点已知，可求直线PC的解析式，同理可求直线PA的解析式；直线PC与x轴的交点B的坐标就可求，直线PA与抛物线y=x2+1的交点Q的坐标就可求，点B、点Q的横坐标是否相同也就显而易见。

已知两点求直线的解析式、求已知直线和x轴的交点、求已知直线和抛物线的交点都是在函数这个单元必须熟练掌握的基础知识，为什么就把学生难倒了呢？原因就是运算繁杂。

基于以上原因和类似题目，本人认为应从以下几方面入手解决这个问题：

1.引导学生平时多动笔，繁杂运算需要完整的解题过程，清晰的思路，每个题目都必须获得答案才算是完成任务。

2.训练好最基本的数学知识，也就是我们平时所讲的数学双基，让学生相信所有的命题都来源于对双基的测试，再繁杂的题目都可以分解为几个简单的双基组合，万变不离其宗，以不变应万变。

3.熟记数学模型。

4.克服畏惧心理因素，培养解决问题的兴趣，相信自己的能力。

5.解题的目标指向要明确，弄清楚题目考查的知识点及该使用的基本技能。