基于分层处理的短码直扩信号盲解扩算法

罗名君，史英春，张 旻

(1.解放军电子工程学院，安徽 合肥 230037; 2.安徽省电子制约技术重点实验室，安徽 合肥 230037)

基于分层处理的短码直扩信号盲解扩算法

罗名君1,2，史英春1,2，张 旻1,2

(1.解放军电子工程学院，安徽 合肥 230037; 2.安徽省电子制约技术重点实验室，安徽 合肥 230037)

针对实际截获的短码直扩(Direct Sequence Spread Spectrum,DSSS)信号信噪比存在波动、以及在低信噪比下伪噪声(Pseudo Random,PN)码盲估计困难的问题，提出了分层解调与解扩的处理方法。该算法将信噪比存在较大起伏的信号分为两层进行处理，首先从筛选出的高信噪比信号中估计扩频周期、短码序列起始位两个参数，然后利用估计出的参数，通过滑动窗口法实现全部信号的盲解扩。算法直接对调制过的BPSK信号进行处理，不需要数字相干信号、不需要估计PN码序列。仿真实验表明，用于参数估计的部分信号信噪比为0 dB时，可以实现信噪比大于等于-12 dB的信号的准确解扩。

短码直扩信号；盲解扩；参数估计；分层处理；滑动窗口法

0 引言

直接序列扩频是一种重要的扩频方式，具有保密性强、抗窄带干扰、抗多径效应、抗频率选择性衰落、可多址复用等优点，广泛应用于无人机、卫星测控等军用及民用通信领域。直扩信号典型特征是利用高速率的扩频码序列与被传输的信息码元相乘，使得信号频谱被展宽，合作接收方可以利用扩频码带来的扩频增益，将有用信息从噪声中提取出来。而对于无线电频谱监管、通信对抗等非合作通信的情况，低信噪比下的盲解扩问题是一个难点，也是当前国内外研究的热点之一。

通常直扩系统采用周期性PN序列作为扩频码序列，根据信息码元宽度与PN序列周期的相对长度，可以将直扩信号分为长码和短码两大类。其中短码直扩信号的信息码元宽度等于PN码周期，其盲解扩的基本思路是先精确估计PN码，实现同步后利用合作解扩的方法得到解扩输出。目前，针对短码DSSS信号的扩频波形估计问题已取得了大量研究成果[1-6]，在低信噪比下可实现PN码波形的精确估计[7]，虽然这些算法逐渐提高了PN码序列的估计精度，但以上文献均假设信号是码片速率采样的基带直扩信号，这样的假设给算法的实际应用带来了一定困难。针对以上问题，本文提出了一种针对短码直扩信号的分层盲解扩算法。

1 理论基础

1.1 信号模型

短码BPSK/DSSS信号表达式为[8]：

(1)

(2)

(3)

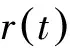
(4)

图1 短码直扩采样信号的结构
Fig.1 Structure of digital medium-frequency short-code DSSS signals

1.2 分层处理的总体思路

由于信号发射、接收平台(典型的如无人机等)的运动性、信道中存在时变噪声等因素，非合作接收方截获的信号的信噪比会存在较大起伏，根据信号的这一特性可以进行分层处理，总体思路如图2所示。

先将信号筛选成两层，从信号中选择一段信噪比较高的部分，估计出扩频周期N(即每个信息码字被采样的次数)及短码序列的起始位；然后通过滑动窗口法对全部信号进行解扩。其中信号筛选是通过直接观察时域/频域波形、噪声估计[10-12]等方法，从截获信号中分离出信噪比较高的一段信号的过程。

2 短码直扩信号的分层盲解扩算法

2.1 参数估计

2.1.1 扩频周期估计

周期平稳过程与其自相关函数具有相同的周期，利用这一性质可以从质量较好的部分信号中估计出扩频周期[8]。若直接对信号进行自相关运算，谱峰搜索函数的峰值容易淹没在噪声中；相关函数二阶矩法[12]使用集平均的方法对噪声进行平滑，同时使相关峰更加突出，算法模型如图3所示[13]。

算法首先将信号等分成M段，分别求自相关函数的模平方后再取平均，最后通过谱峰搜索估计扩频周期。对于输入是数字信号的情况，算法表达式为：

(5)

(6)

2.1.2 短码序列起始位估计

从短码DSSS采样信号中任意位置连续截取两个长度为N的样本矢量w1、w2，见图4。

由于取样位置是任意的，不失一般性，仅考虑其在某一完整码字rk上的情况。在rk上遍历取样位置w1，则不同码字组合下w1·w2的取值曲线如图5所示：(仿真信号参数：PN码：1 023位Gold码，数据速率：12.8 Kb/s，码片速率：13.094 4 Mc/s，载频：26.188 8 MHz，采样率：48.012 8 MHz，无噪声；原图彩色，4种不同形状的曲线代表不同的码字组合。)

改变各项参数重新仿真的结果类似，仅曲线最大、最小值不同。由图5可以得出以下结论：

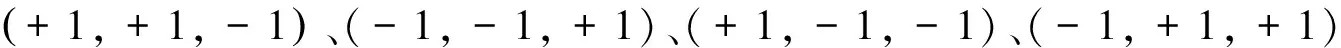
2) 估计误差小于N/2时，可以通过w1·w2的符号判断dkdk+1的相对极性。

实际应用中w1的遍历起点在某一完整码字rk上是均匀分布的，此时w1·w2的变化曲线为图5中任意两种曲线的组合。由结论1)得出，只要两段曲线不是相同的常值函数，就可以将曲线类型的转换点估计为当前短码序列的起始位。算法流程如图6所示。

2.2 滑动窗口法解扩原始信号

2.2.1 算法原理

短码BPSK/DSSS信号具有图7所示的时域特征。

不同码字对应的短码序列波形相位相差π。因此，任意两个码字dmdn的相对极性可以通过各自采样序列rmrn内积的符号进行判断：

(7)

由于已经从一段信噪比较高的信号中估计出了伪码周期以及短码序列起始位，可以取出一整周期的短码序列rp作为滑动窗口解扩原始信号。原始信号中任意第k个码字估计如下：

(8)

使rp以伪码周期N为步进，从原始信号的第一个短码序列起始点开始滑动，同时按照式(8)进行计算则可以得到全部信号的盲解扩输出。

2.2.2 算法总体步骤

基于分层处理的短码BPSK/DSSS信号盲解扩算法总体步骤如下：

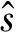
4)初始化迭代次数i=1；

3 仿真实验与结果分析

参照实际无人机上行链路遥控信号，短码BPSK/DSSS信号参数设置如表1所示。

表1 仿真信号参数设置

3.1 实验1PN码周期估计算法验证

信噪比SNR=-10dB，分别采用直接自相关法与相关函数二阶矩法对信号进行处理，得到谱峰搜索函数如图8所示。

对比图8(a)、(b)可知，相关函数二阶矩法具有更强的抗噪声能力。

3.2 实验2PN码周期估计算法性能

以“估计误差=0”作为有效估计的标准，在不同信噪比下分别进行500次MonteCarlo实验，正确率随信噪比的变化曲线如图9所示。

从图中可以看出，信噪比大于等于-12dB时，PN码周期估计的正确率可以达到100%，这表明相关函数二阶矩法具有较强的抗噪声能力。

3.3 实验3 短码序列起始位估计算法性能

以“估计误差=0”作为有效估计的标准，在不同信噪比下分别进行500次MonteCarlo仿真实验，正确率随信噪比的变化情况如图10所示。

从图中可以看出，信噪比大于等于19dB时，短码序列起始位估计正确率可以达到100%。与实验2中的算法相比该算法对噪声更加敏感，这是因为该算法参与运算的数据量较少，没有对噪声进行平滑。

3.4 实验4 盲解扩算法总体性能

用于参数估计的部分信号的信噪比为0dB；以误码率作为解扩性能指标，在不同信噪比下分别进行500次MonteCarlo仿真实验，得到的性能曲线图11所示。

结合图10、图11可以看出，虽然信噪比大于、等于19dB时短码序列起始位估计算法才能实现100%的正确率，但只要信噪比大于等于-12dB，本文算法就能实现0误码率，这表明解扩算法可以抵御较大的短码序列起始位估计误差。

4 结论

本文提出了基于分层处理的短码直扩信号盲解扩算法。该算法将信噪比存在较大起伏的信号分为两层进行处理：首先从筛选出的高信噪比信号中估计扩频周期、短码序列起始位两个参数，然后利用估计出的参数，通过滑动窗口法实现全部信号的盲解扩。算法直接对调制过的BPSK信号进行处理，不需要数字相干信号、不需要估计PN码序列。仿真实验表明，用于参数估计的部分信号信噪比为0dB时，可以实现大于等于-12dB信噪比信号的准确解扩。

下一步拟对非整数倍码片速率采样的短码直扩信号的盲解扩问题展开研究。

[1]BouderC,AzouS,BurelG.Arobustsynchronizationprocedureforblindestimationofthesymbolperiodandthetimingoffsetinspreadspectrumtransmissions[C]//IEEESeventhInternationalSymposiumonSpreadSpectrumTechniquesandApplications.US:IEEE, 2002:238-241.

[2]BouderC,AzouS,BurelG.Performanceanalysisofaspreadingsequenceestimatorforspreadspectrumtransmissions[J].JournaloftheFranklinInstitute, 2004, 341(7):595-614.

[3]TsatsanisMK,GiannakisGB.Blindestimationofdirectsequencespreadspectrumsignalsinmultipath[J].SignalProcessingIEEETransactionson, 1995, 45(5):403.

[4]PengY,TangB,LuM.FastmethodforspreadingsequenceestimationofDSSSsignalbasedonmaximumlikelihoodfunction[J].JournalofSystemsEngineering&Electronics, 2010, 21(6):948-953.

[5]付卫红, 杨小牛, 刘乃安. 基于盲源分离的CDMA多用户检测与伪码估计[J]. 电子学报, 2008, 36(7):1319-1323.

[6]任啸天, 徐晖, 王翔,等. 一种针对短码、周期长码直扩信号扩频序列盲估计方法[J]. 宇航学报, 2011, 32(12):2596-2600.

[7]张花国, 李鑫, 张建华,等. 基于半定松弛的长码DSSS信号扩频波形估计[J]. 电子学报, 2016, 44(2):334-339.

[8]张天骐.直扩信号的盲处理[M].北京：国防工业出版社,2012.

[9]谢然, 张效义, 田鹏武. 一种基于循环谱的MPSK信号符号速率估计方法[J]. 计算机应用研究, 2011, 28(6):2294-2296.

[10]邓自立,许燕.基于Kalman滤波的白噪声估计理论[J].自动化学报,2003,29(1):521-524.

[11]孟宪波,鲍长春.基于最小控制GARCH模型的噪声估计算法[J].电子学报,2016,44(3):747-752.

[12]劳子轩,刘子扬,彭涛,等.全盲频谱感知:噪声估计与能量检测联合迭代算法[J].电子与信息学报,2013(8):1958-1963.

[13]张雪梅.直扩信号检测与参数估计方法研究[D].西安：西安电子科技大学,2014.

A Blind Despreading Algorithm for Short-code BPSK/DSSS SignalsBased on Hierarchical Processing

LUO Mingjun1,2,SHI Yingchun1,2,ZHANG Min1,2

(1.Electronic Engineering Institute of PLA, Hefei 230037, China; 2.Key Laboratory Electronic Restricting Technique, Hefei 230037, China)

Aiming at the fact that the signal-to-noise ratio(SNR) of real BPSK/DSSS signal often undulates, and that it is hard to estimate the pseudo-noise sequence under severe noisy circumstances, a method which hierarchically demodulate and despread signal was proposed. The algorithm firstly figured out the pseudo-noise sequence by using a sample from the received signal with high SNR, where coherent demodulation was employed. Then, by using the estimated pseudo-noise sequence the entire signal could be despread and demodulated in a cooperative way. Simulation showed the algorithm’s performance curves under various SNR values, and the results showed that, by using the proposed method, effective despreading could be achieved when treating signal with undulating SNR values.

BPSK/DSSS; software demodulation; pseudo-noise sequence estimation;autocorrelation

2016-07-02

国家自然科学基金项目资助(60972161)；安徽省自然科学基金项目资助(1408085QF115)

罗名君(1993—)，男，湖南张家界人，硕士研究生，研究方向：通信信号分析与处理。E-mail: luomingjuncl@163.com。

TP391.41

A

1008-1194(2017)01-0026-05