冷整形对大模数直齿轮精度的影响

梁强，周杰，朱姗姗，曹金豆



冷整形对大模数直齿轮精度的影响

梁强，周杰，朱姗姗，曹金豆

(重庆大学材料科学与工程学院，重庆，400044)

为提高大模数圆柱直齿轮冷整形后的精度，以实测齿轮预锻件形状尺寸为基础，建立基于误差模型的直齿轮冷整形过程的弹塑性有限元仿真模型，通过数值模拟得到精整量和精整凹模定径带长度对齿轮齿廓总偏差和螺旋线总偏差的影响规律。对直齿轮冷整形工艺进行实际验证，并对整形后齿轮的检测数据进行方差分析。研究结果表明：精整量对齿轮精度影响显著；当精整量为0.15~0.20 mm时，通过冷整形可以获得齿形精度为8级、齿向精度为7~8级的齿轮；工艺实验得到的齿轮偏差与模拟结果变化趋势一致。

大模数直齿轮；冷整形；齿轮精度；数值模拟

随着齿轮成形工艺研究的深入和市场需求的不断增大，现代制造业对齿轮产品精度要求不断提高，齿轮的精密成形一直人们的研究热点[1−2]。大模数直齿轮作为大型重载机械中重要的零部件，其强度与精度成为加工制造的关键。目前，大模数直齿轮精密成形工艺主要有“温锻+冷整形”复合工艺和“冷挤压−冷整形”复合工艺。温冷复合工艺具有成形力小、模具寿命长的优点，但温锻齿坯后需要中间几道工序处理后才能冷整形，工艺较冗杂。随着新型高强度冷作模具钢的应用，冷挤压逐渐成为齿轮精密成形的主要工艺，挤齿后齿面光洁，经润滑可以直接冷整形，精整后精度高，表面质量好。在冷挤压−冷整形过程中，冷整形是保证成形精度的关键工艺。朱怀沈等[3−5]对温冷复合工艺下精整量对齿轮精度的影响进行了研究，但均采用无误差模型进行精整模拟及实验。STONE 等[6−7]对冷整形后单齿表面质量及齿形尺寸进行了研究，但未考虑精整量对齿轮精度的影响。胡成亮等[8−10]则对直齿轮1次冷精锻成形进行了数值模拟和实验研究，锻后齿轮填充饱满，但并未对精度进行分析。为此，本文作者采用弹塑性有限元法，以模数=4，齿数=16，压力角=20°，变位系数=0.45的齿轮为研究对象，建立直齿轮冷整形有限元模型，研究精整量及精整凹模定径带长度对冷整形后齿轮精度的影响；同时，通过工艺实验进行验证，得出直齿轮冷整形最佳的精整量和精整凹模定径带长度。

1 工艺方案

直齿轮成形工艺为热锻制坯—球化退火—抛丸—车削制坯—磷化皂化—冷挤压—冷整形，材料为20CrMnTi。冷挤压和冷整形均采用通过式的成形工艺，如图1所示。

冷挤压后的齿轮如图2所示，齿轮上端与下端齿顶部分(见图2(b))均出现填充不饱满的现象，上端不饱满长度为1.5~2.0 mm，上端端面(见图2(a))凹陷约2.0 mm，并且存在纵向毛刺；下端不饱满长度为2.0~3.0 mm下端端面(见图2(c))外凸约1.5 mm。导致冷挤压齿轮上、下端充填不饱满的原因主要是挤压时上、下端均处于无约束状态，金属填充模具能力弱。由于在设计挤压凹模时对齿形进行修形，故挤压件车外圆后齿顶可满足设计尺寸要求。

在齿轮测量中心检测冷挤压齿轮的精度，齿轮精度检测的2个重要指标为齿廓总偏差和螺旋线总偏差[11]，测量结果见表1。冷挤压齿轮的精度较低，未能达到精锻齿轮设计的精度要求，只能作为预锻件，故需要增加冷整形工艺来提高冷挤压齿轮的精度。

(a) 冷挤压工艺示意图；(b) 冷整形工艺示意图

表1 齿轮精度检测报告

(a) 上端；(b) 正面；(c) 下端

2 有限元模型建立及工艺实验

2.1 有限元模型建立

朱怀忱等[3−5]建立的整形模型均为无误差的理想模型，即整形前齿轮的齿廓总偏差和齿形总偏差均为0 μm，这与实际情况并不吻合。为了建立与实际情况相吻合的模型，需要测量挤压后齿轮的尺寸。随机选择3个挤压后的齿轮，使用公法线千分尺跨3齿测量5组沿齿宽不同截面的公法线长度，每个截面测量3组不同的齿并求平均值，换算后得到沿齿宽方向齿厚度的变化。图3所示为冷挤压齿轮沿齿宽方向齿厚度的变化，齿轮中部齿厚度较上、下端均小，下端即先挤出端齿厚度最大。由于齿根部分不影响齿轮精度，齿顶后续要车外削加工，故冷整形只精整齿面，齿根和齿顶部分不进行精整。

以实测齿厚分别建立三维模型和有限元模型。由于冷整形是小变形，故齿轮预锻件定义为弹塑性体，材质为20CrMnTi；为提高计算精度，采用六面体单元对齿轮预锻件进行网格划分，并对齿形部分进行网格局部细化；模具定义为刚体，忽略模具的弹性变形；设备选用液压机，凸模运动速度设为20 mm/s；预锻件整形前需经磷化皂化润滑处理，故摩擦因数选择0.12，服从剪切摩擦模型；为了提高计算效率，取单齿进行模拟，有限元模型如图4所示。为研究精整量和精整凹模定径带长度对齿轮精度的影响规律，以实测的齿轮预锻件平均齿厚度作为基准设计整形模具，选择不同的精整量和定径带长度进行数值模拟，模拟实验方案如表2所示。对模拟结果进行量化处理，处理方法如下：在渐开线齿面上选取所有节点进行跟踪，并获得整形后节点的坐标信息，导入CATIA中进行齿面重建，测量其螺旋线总偏差和齿廓总偏差。

图3 齿轮预锻件沿齿宽方向齿厚的变化

图4 有限元模型

表2 模拟实验方案

2.2 工艺实验

工艺实验在四柱液压机上进行，精整凹模采用组合式凹模。为节约实验成本，先加工单边精整量为 0.3 mm的整形凹模进行实验，整形凹模定径带长度为20 mm，实验完成后在线切割机床上对模具精整工作带进行慢走丝加工，加工至单边精整量分别为0.25，0.20，0.15和0.10 mm后再次进行整形实验，整形凹模如图5所示。由于不同定径带长度的凹模加工费用高，故未进行工艺实验。

(a) 整体；(b) 细节

利用齿轮测量中心对不同精整量整形后的齿轮进行检测，对每个精整量的齿轮分别抽选3个进行测量，每次测量随机取3个齿，并对测量结果进行方差分析。

3 结果比较与分析

3.1 精整量对齿轮精度的影响规律

精整量是冷整形工艺的重要工艺参数之一，直接影响整形后齿轮的精度。表3所示为实测齿廓总偏差和实测螺旋线总偏差随精整量变化的方差齐性检验结果，可见当前自由度下对应的显著性分别为0.220和0.062，均大于0.050，可以认为样本来自的总体满足方差齐性的要求[12−13]。表4所示为实测齿廓总偏差和实测螺旋线总偏差随精整量变化的方差分析结果，显著性均小于0.001，说明精整量对齿廓总偏差和螺旋线总偏差有显著性影响。

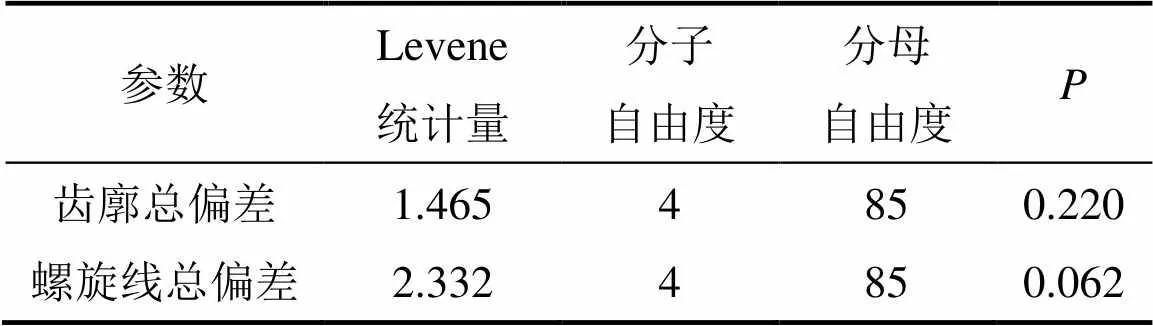
表3 方差齐性检验结果

由有限元计算和实验所得到的齿廓总偏差与螺旋线总偏差随精整量的变化分布见图6。从图6可见：与数值模拟结果相比，实测齿轮偏差偏大，但变化趋势相吻合，误差主要源于工艺实验中模具弹性变形引起的尺寸误差。

图6(a)所示为齿廓总偏差随精整量的变化，可见齿廓总偏差总体上随着精整量的增大而增大，精整量在0.1~0.2 mm间齿廓总偏差稳定，精整量大于0.2 mm后齿廓总偏差变大。图6(b)所示为螺旋线总偏差随精整量变化。从图6(b)可见：螺旋线总偏差随着精整量的增加先减小后增大，精整量在0.15~0.20 mm区间内冷整形后齿向精度最高；当采用较小的精整量整形齿件时，齿件经过整形模具发生微小塑性变形甚至只有弹性变形，当模具的约束消失后便发生弹性回复，齿面不能得到有效整形，故过小的精整量并不能有效提高齿轮精度；当采用过大精整量整形齿件时，变形区域变大，齿面发生剧烈的塑性变形，达不到齿形精整的目的。综合以上分析，齿件单边精整量为0.15~ 0.20 mm时为宜。

(a) 齿廓总偏差；(b) 螺旋线总偏差

表4 方差分析结果

注：括号内数据为组间值；括号外数据为组内值。

3.2 定径带长度对齿轮精度的影响规律

凹模定径带是影响齿轮成形质量的重要工艺参数之一[14−15]。图7(a)所示为数值模拟计算的齿廓总偏差随定径带长度的变化，可见齿廓总偏差随着定径带长度的增大而减小，定径带长度超过20 mm后齿廓总偏差稳定在0.02 mm。图7(b)所示为数值模拟计算的螺旋线总偏差随定径带长度的变化，螺旋线总偏差随着定径带长度的增大而减小，定径带长度超过20 mm后螺旋线总偏差稳定在0.006 mm。

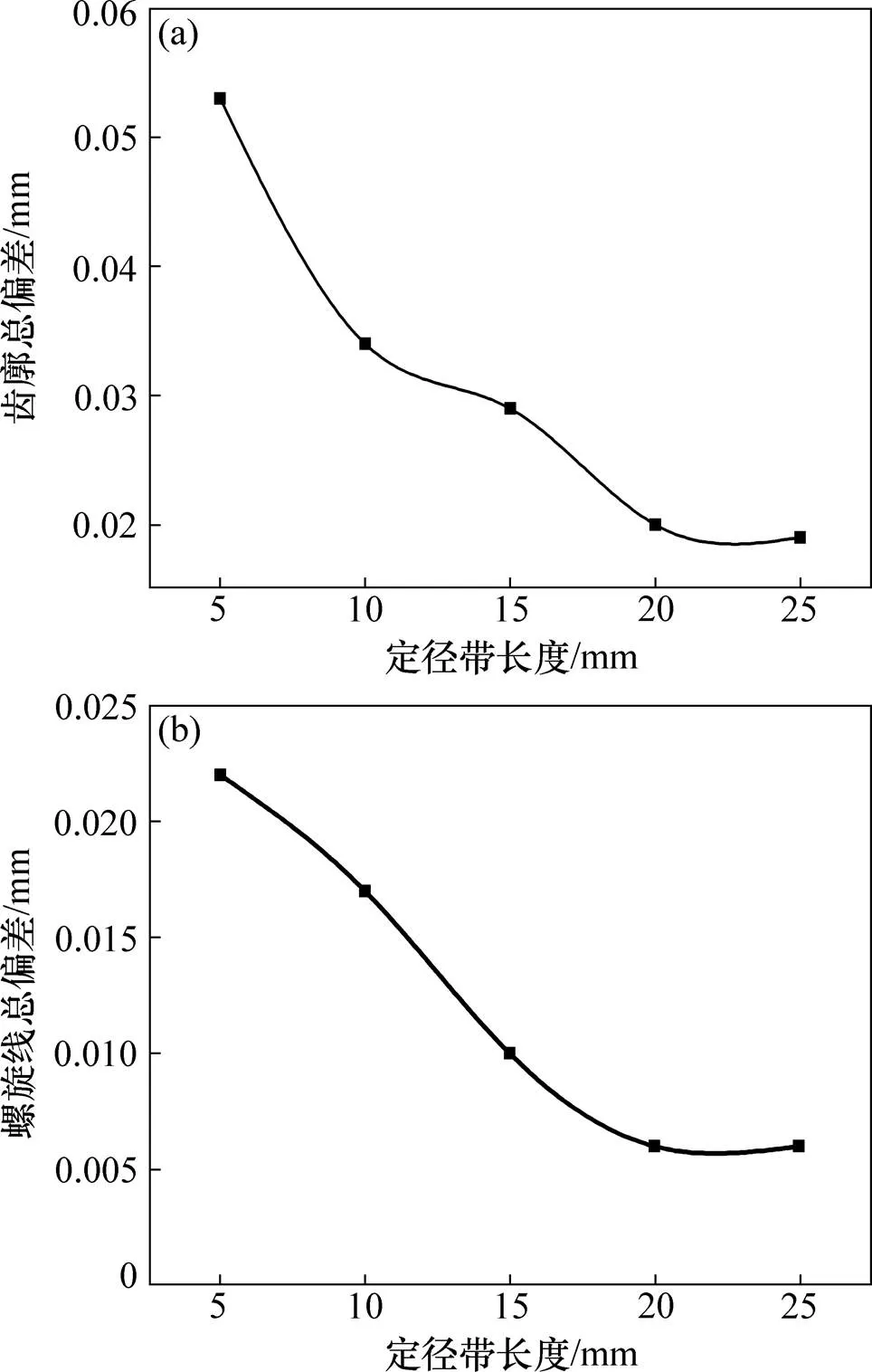
(a) 齿廓总偏差；(b) 螺旋线总偏差

不同定径带长度的等效应力场见图8。从图8可见：当定径带长度为5 mm时，齿面塑变区超过定径带长度(见图8(a))，齿件通过模具后仍会发生变形，故整形后齿轮精度较低；当定径带长度分别为20 mm和25 mm时，齿面塑变区在定径带长度范围内(见图8(b)和8(c))，齿面塑性变形后在定径带内只进行刚性移动。故当定径带达到20 mm后，齿轮精度便达稳定值。

3.3 冷整形实验结果

图9(a)所示为采用精整量0.2 mm和定径带长度20 mm冷整形后的实验结果，冷整形后齿件齿宽为61~63 mm。齿件经车两端面、镗内孔、车外圆和倒棱后，机加后齿件齿宽56.40~56.45 mm，齿形充填饱满，齿形精度和齿向精度均达到8级，较冷整形前齿轮精度显著提高，如图9(b)所示。

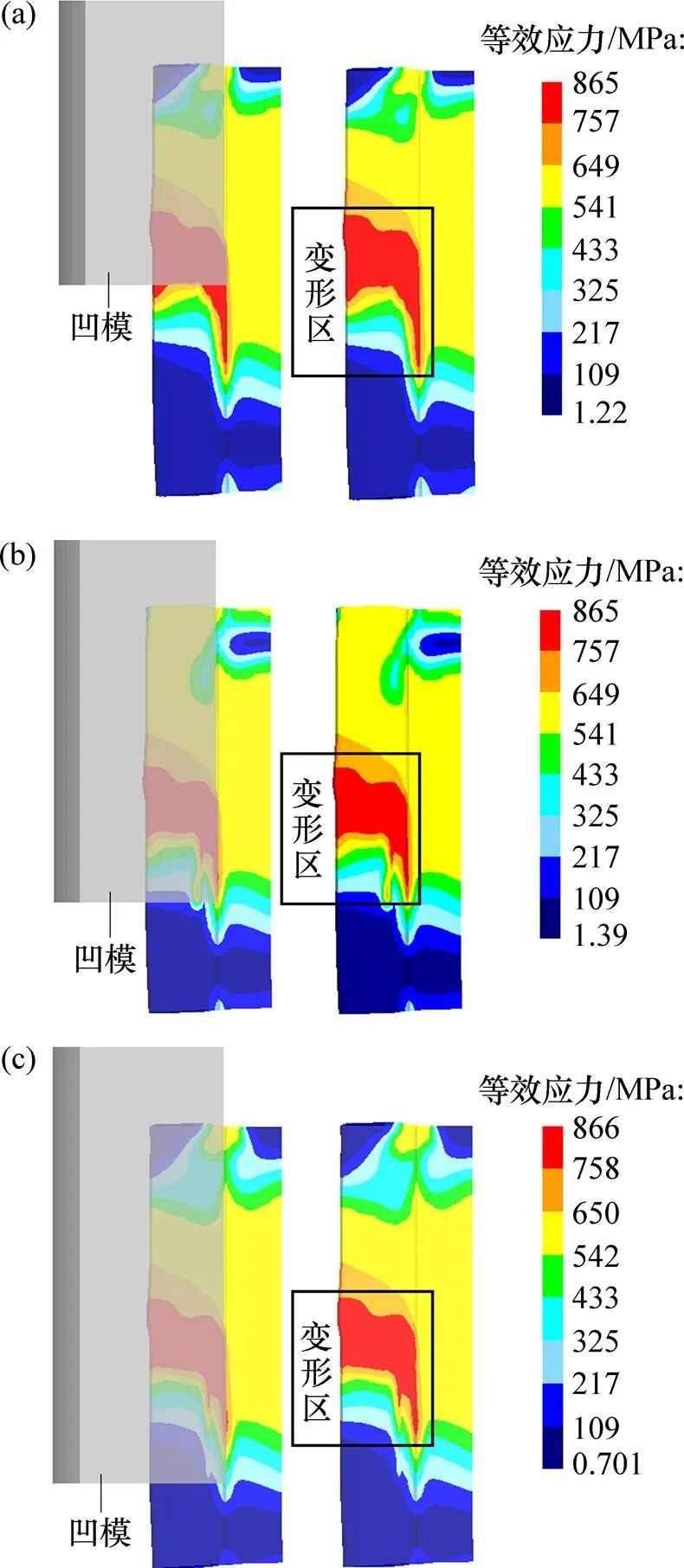
定径带长度/mm：(a) 5；(b) 20；(c) 25

(a) 冷整形后齿件；(b) 机械加工后齿件

4 结论

1) 以实际测量的冷挤压齿轮数据建立误差模型，数值模拟得到的精整量与齿轮精度间的规律与工艺实验结果趋势一致，模拟结果与实验结果虽然在数值上有些差异，但总体来看能反映精整量与成形精度间的规律，说明建立的基于实测误差模型的直齿轮预锻件冷整形弹塑性有限元模型是正确的。

2) 齿廓总偏差随精整量的增大而增大，螺旋线总偏差随精整量的增大先减小后增大，精整量合理范围为0.15~0.20 mm。采用精整量为0.2 mm，凹模定径带长度20 mm的工艺参数进行工艺实验，冷整形后能够获得齿形精度为8级、齿向精度为7~8级的齿轮。

3) 齿廓总偏差和螺旋线总偏差随凹模定径带长度增加而减小，并在定径带长度大于20 mm时达到稳定值。

[1] 冯再新, 周贤宾, 张治民, 等. 齿轮精密成形精整毛坯设计[J]. 塑性工程学报, 2006, 13(1): 67−70. FENG Zaixin, ZHOU Xianbin, ZHANG Zhimin, et al. Designing of semifinished product for spur gear precision forming[J]. Journal of Plasticity Engineering, 2006, 13(1): 67−70.

[2] 周瑞, 陈文琳, 李亨, 等. 基于弹性变形行为的冷精整直齿轮尺寸预测[J]. 塑性工程学报, 2013, 20(5): 27−32. ZHOU Rui, CHEN Wenlin, LI Heng, et al. Demension prediction of spur gear in cold precision sizing based on elastic deformation behavior[J]. Journal of Plasticity Engineering, 2013, 20(5): 27−32.

[3] 朱怀沈, 夏巨谌, 金俊松, 等. 大模数直齿轮温冷锻精整量的优化选择[J]. 塑性工程学报, 2011, 18(1): 53−57. ZHU Huaishen, XIA Juchen, JIN Junsong, et al. Optimization of sizing amount during warm-cold compound forging for spur gear with big modulus[J]. Journal of Plasticity Engineering, 2011, 18(1): 53−57.

[4] 谢晋市. 大模数直齿轮温冷复合精密成形工艺研究[D]. 合肥: 合肥工业大学材料科学与工程学院, 2012: 1−67. XIE Jinshi. Research on the warm-cold composite precision forming process of large module spur gear[D]. Hefei: Hefei University of Technology. School of Materials Science and Engineering, 2012: 1−67.

[5] 张宝红. 高性能直齿圆柱齿轮开放成形研究[D]. 太原: 中北大学材料科学与工程学院, 2005: 12−17. ZHANG Baohong. Study on opened-die forming for high property spur gear[D]. Taiyuan: North University of China. School of Materials Science and Engineering, 2005: 12−17.

[6] STONE E R H, CAI J, HU Z M. An exercise in cold ironing as the post-forging operation for net-shape manufactures[J]. Journal of Materials Processing Technology, 2002, 135(2): 278−283.

[7] CHANG Y C, HU Z M, KANG B S. A study of cold ironing as a post-process for net-shape manufactures[J]. International Journal of Machine Tools & Manufacture, 2002, 42(8): 945−952.

[8] 胡成亮, 施卫兵, 徐翔龙, 等. 带毂直齿轮冷精锻新工艺及其数值模拟[J]. 上海交通大学学报, 2009, 43(9): 1494−1497. HU Chengliang, SHI Weibing, XU Xianglong, et al. A novel cold precision forging process of spur gear with boss and its numerical simulation[J]. Journal of Shanghai Jiaotong University, 2009, 43(9): 1494−1497.

[9] CHOI J C, CHOI Y. Precision forging of spur gears with inside relief[J]. International Journal of Machine Tools & Manufacture, 1999, 39(10): 1575−1588.

[10] EYRCIOGLU O, KUTUK M A, YILMAZ N F. Shrink fit design for precision gear forging dies[J]. Journal of Materials Processing Technology, 2009, 209(4): 2186−2194.

[11] 朱孝录. 齿轮传动设计手册[M]. 北京: 化学工业出版社, 2010: 234−265. ZHU Xiaolu. Handbook of gear design[M]. Beijing: Chemical Industry Press, 2010: 234−265.

[12] 杨虎, 刘琼荪, 钟波. 数理统计[M]. 北京: 高等教育出版社, 2004: 153−154. YANG Hu, LIU Qiongsun, ZHONG Bo. Mathematical statistics[M]. Beijing: Higher Education Press, 2004: 153−154.

[13] 刘文卿. 实验设计[M]. 北京: 清华大学出版社, 2005: 23−26. LIU Wenqing. Design of experiments[M]. Beijing: Tsinghua University Press, 2005: 23−26.

[14] 冯文杰, 辜志勇, 陈莹莹. 定径带长度对花键轴冷挤压弯曲变形的影响[J]. 现代制造工程, 2011(10): 97−99. FENG Wenjie, GU Zhiyong, CHEN Yingying. The influence of die bearing length on bending deformation of spline shaft in cold extrusion[J]. Modern Manufacturing Engineering, 2011(10): 97−99.

[15] 辜志勇. 花键轴冷挤压弯曲变形研究[D]. 重庆: 重庆理工大学重庆汽车学院, 2012: 51−74. GU Zhiyong. Research on bending deformation of spline shaft in cold extrusion[D]. Chongqing: Chongqing University of Technology. College of Chongqing Automobile, 2012: 51−74.

(编辑 陈灿华)

Influence of gear accuracy in cold precision sizing for spur gear with big modulus

LIANG Qiang, ZHOU Jie, ZHU Shanshan, CAO Jindou

(College of Material Science and Engineering, Chongqing University, Chongqing 400044, China)

In order to improve gear accuracy in cold precision after cold precision sizing, an elastic plastic FE model based on the measured gear shape of pre-forging was built to simulate the cold precision sizing process. The laws of sizing amount and die bearing length on the tooth profile total deviation and the tooth orientation total deviation were obtained by numerical simulation. The experiment of the spur gear cold precision sizing process was made and data were analyzed by analysis of variance (ANOVA). The results show that the sizing amount has significant effects on gear accuracy. When the sizing amount is 0.15−0.20 mm, the gear of the tooth profile accuracy with 8 magnitudes and the gear direction precision with 7−8 magnitudes are obtained through the cold precision sizing. The change tendency of the deviation of gear obtained by experiment is similar to the FEM result.

spur gear with big modulus; cold precision sizing; gear accuracy; numerical simulation

10.11817/j.issn.1672−7207.2017.02.006

TG316

A

1672−7207(2017)02−0310−06

2016−03−05；

2016−05−22

国家自然科学基金面上项目(51275543)；重庆市科委应用开发项目(cstc2014yykfC70003)(Project(51275543) supported by the National Natural Science Foundation of China; Project(cstc2014yykfC70003) supported by the Science and Technology Application Development of Chongqing Municipal)

周杰，博士，教授，从事体积精密成形研究；E-mail：woliangniliu@163.com