隔膜压滤机污泥脱水工作流程优化

朱桂华，高明泉，马凯，唐啸，朱天宏，徐洪威



隔膜压滤机污泥脱水工作流程优化

朱桂华，高明泉，马凯，唐啸，朱天宏，徐洪威

(中南大学机电工程学院，湖南长沙，410083)

针对隔膜压滤机各工作流程阶段污泥的过滤性能，运用Fluent软件数值模拟隔膜压滤机压滤过程，研究污泥二相流在隔膜压滤机深度脱水过程中滤液总量随时间变化的规律，并采用最小二乘法拟合其关系曲线。通过仿真分析，提出隔膜压滤机鼓膜阶段的虚拟滤液量法的概念，并以此推导鼓膜阶段实际滤液总量3与压滤时间的数学关系表达式，描述两者的影响关系，进而得到隔膜压滤机工作效率的计算公式；利用该公式对某污泥处理厂隔膜压滤机各工作阶段时间进行优化计算。研究结果表明：对于规格一定的隔膜压滤机，其压滤阶段时间是压滤机工作效率的决定因素；利用本文方法计算的某污泥处理厂隔膜压滤机各工作阶段时间，污泥处理工作总效率提高37.7%，为隔膜压滤机进行污泥脱水找到了最佳作业流程时间，大大提高了作业效率。

隔膜压滤机；最小二乘法；最佳压滤时间；比过滤速度

隔膜压滤机的核心构件过滤板组由一组两侧内凹的普通滤板与一组两侧附有隔膜的隔膜板交替组合而成[1−2]。滤板的凹槽部分与隔膜板结合形成滤室。滤室附有滤布，污泥二相流在进料泵压力作用下，通过滤布达到固液二相分离的目的[2]。由于其耐高压，密封性好，卸料方便，滤饼含水率低，隔膜压滤机广泛应用于冶金、化工、煤炭和污泥处理等领域[3]。目前，国内污泥处理厂对隔膜压滤机各工作流程时间设定主要凭借经验，具有粗放性和随意性的弊病，导致压滤机工作周期长、效率低。而国内外对于隔膜压滤机污泥脱水性能的理论研究大多局限于依据达西定理，对进料压滤阶段的过滤特性规律建立数学模型，但对过滤特性变化复杂的鼓膜压榨阶段研究较少。刘鹏等[4]对过滤过程中滤饼比阻的测量方法以及对滤饼恒压过滤的影响因素进行了研究，但该方法并不适用于隔膜压滤机的鼓膜压榨阶段；赵扬等[5]通过对不同鼓膜压榨起始点进行试验，表明不同起始压榨点对过滤有较大影响，但该方法基于大量实验总结规律，并未建立鼓膜压榨阶段滤液量随时间变化的数学模型，没有提出一种理论计算方法；STICKLAND等[6]对固定滤室的板框压滤机进行了过滤研究，滤液量与时间的斜率起初增大，随后相应的斜坡压力和滤室阻力增大，最后滤饼压力恒定，形成滤饼。该研究也未涉及隔膜压滤机的鼓膜压榨阶段。为此，本文作者利用Fluent软件模拟压滤机压滤阶段，依据所得结果，通过数学拟合的方法建立压滤机各个工作过程的数学模型。提出“虚拟滤液量法”，描述过滤变化较复杂的鼓膜阶段滤液量随时间变化的数学模型，进而达到优化隔膜压滤机各工作阶段时间、提高压滤机工作效率的目的。

1 隔膜压滤机工作流程及原理

隔膜压滤机工作周期分为进料阶段、压滤阶段、鼓膜阶段、反吹阶段、卸料阶段以及为下一次工作周期进行清洗滤布、压紧滤板等工作的准备阶段。

隔膜压滤机工作周期时间轴如图1所示。反吹、卸料和准备阶段时间一定，为方便计算将其整合，称为0。

进料阶段时间1从污泥泵送至压滤机开始，至充满整个滤室为止，该阶段时间也为定值。

压滤阶段时间2从0点开始，至2停止，以额定压力2继续入料，并压滤污泥。

鼓膜阶段时间3，压滤机停止进料，隔膜板两侧隔膜以额定压力3(3＞2)注入水或空气使隔膜腔膨胀，压缩滤室内泥饼体积，使泥饼进一步过滤，至3结束。

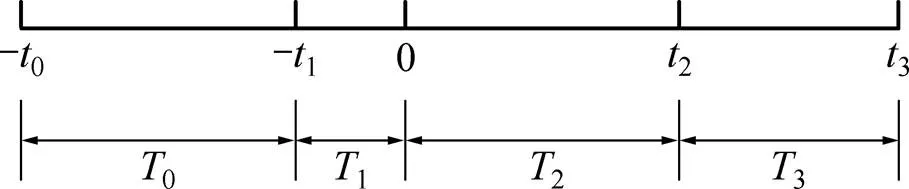
图1 隔膜压滤机工作周期时间轴

由于压滤阶段和鼓膜阶段的过滤速度随着时间的增加而逐渐降低，压滤机工作后期处理污泥的效率也开始下降。因此，可以通过优化压滤时间2和鼓膜时间3，提高隔膜压滤机的工作效率。

2 基于Fluent仿真压滤机工作过程

本次仿真的目的是通过模拟压滤机压滤过程，记录各时间点的滤液量，找到压滤阶段滤液量与时间的变化关系、比过滤速度[2, 7−8]与时间的变化关系以及过滤压力与污泥极限过滤量的变化关系，从而为预测压滤机其他工作阶段的数学模型提供数据依据。

2.1 滤室模型的建立

Fluent前处理采用Gambit软件，建立压滤机单个滤室的几何模型，并对其进行网格划分。计算方法选取“标准−模型”，离散格式选用“QUICK”，压力插值方法选用“PRESTO！”，压力—速度耦合方法采用“PISO”。

其主要参数如下：滤室直径为300 mm；固相颗粒直径为0.01 mm；滤室厚度为10 mm；额定过滤压力为0.2~3.0 MPa；固相密度为1 051 kg/m3；过滤时间为30 min；孔隙率为20%；二相流含水率为95%；惯性阻力系数为3.5×107；黏度阻力系数为1.2×1015；动力黏度为0.02 Pa∙s。

2.2 仿真结果

在0.2~1.4 MPa过滤压力条件下，4组滤液总量与时间的关系如图2所示。从图2可以看出：滤液总量随时间逐渐增大，并趋近于某一极限值；压力越大，滤液速度越快，最终的极限过滤量也越大。

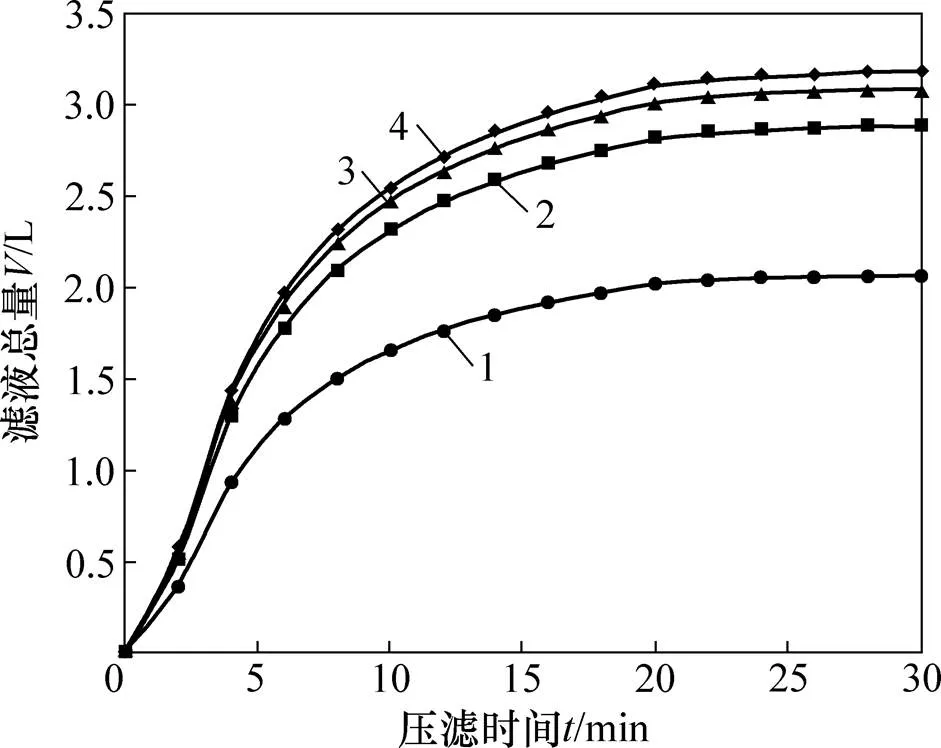
p/MPa：1—0.2；2—0.6；3—1.0；4—1.4。

图3所示为过滤压力为1.4 MPa时，多孔介质外侧横截面液相流速云图。图4所示为比过滤速度与时间关系曲线。从图4可看出：比过滤速度会在起始处激增至某一值，继续上升一小段时间，达到最大值后随时间的增加而逐渐降低；比过滤速度短暂上升的主要原因是污泥微粒在压滤初期黏结，微粒直径增大，导致泥层比表面积减小，孔隙率增大。Kozeny-Carmen方程为[9]：

式中：为固相密度；为Kozeny-Carman常数；为孔隙率；为比表面积。由式(1)可以看出：比阻与比表面积平方成正比，与孔隙率呈负相关。而比阻与泥饼的过滤性能成反比，因此，比过滤速度初期短暂上升，然后，随着比阻增大逐渐下降。

/min：(a) 0；(b) 2；(c) 15；(d) 30

图3 多孔介质横截面液相流速云图

Fig. 3 Cloud maps of fluid velocity on porous intersecting surface

图4 比过滤速度q与时间t的关系

3 二相流过滤数学模型的建立

3.1 传统过滤计算方法

根据达西定理，计算某一时刻比过滤速度方程如下[10]：

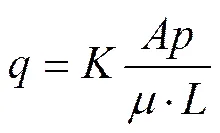
式中：为滤液黏滞性系数；为比过滤速度；为过滤压力；为渗透系数；为过滤面积；为滤室厚度。则过滤量。根据121(1为滤布阻抗，2为泥饼阻抗，为过滤比阻，为单位过滤介质截泥量)，可推导出[10−11]

(3)

传统测量比阻方法通常认为泥饼不可压缩，测量d/d−的曲线斜率[12]。通过推导得到比阻是关于的正比例函数[6, 13]，进而求得泥饼比阻。但该方法视泥饼不可压缩，比阻不随时间变化而改变，这显然与压滤机滤室内污泥二相流的过滤情形不吻合。此外，隔膜压滤机工作流程较多，压滤阶段为定压入料过滤，而鼓膜阶段滤室体积随时间不断变化，造成比阻变化复杂，难以利用式(3)表述−的变化关系。

3.2 基于仿真结果计算方法

通过仿真记录污泥滤液总量()与时间的变化曲线以及比过滤速度与时间的变化曲线，拟合计算得到−函数表达式。

3.2.1 进料阶段

在进料阶段，过滤量近似为0 L。污泥以一定流量进料最终达到1，即为滤室体积。

3.2.2 压滤阶段

由图2可知：在压滤阶段，滤液总量2随时间不断上升。由其导数(图4)可知：首先会有短期上升，然后逐渐降低，并最终趋近于0 L。因此，指数形式比较符合滤液总量随时间的变化规律，可以通过最小二乘法拟合压滤阶段的()−曲线。设

对仿真的0.2~3.0 MPa条件下8组2−曲线通过最小二乘法拟合，所得结果如表1所示。

由表1得过滤压力p与参数2曲线如图5所示。

极限过滤量2随压力增大而增大，但上升速度由快到慢，并趋于定值，达到该定值后，再加大压力并不能使泥饼进一步过滤[14]。

表1 压滤阶段V2(t)−t函数参数

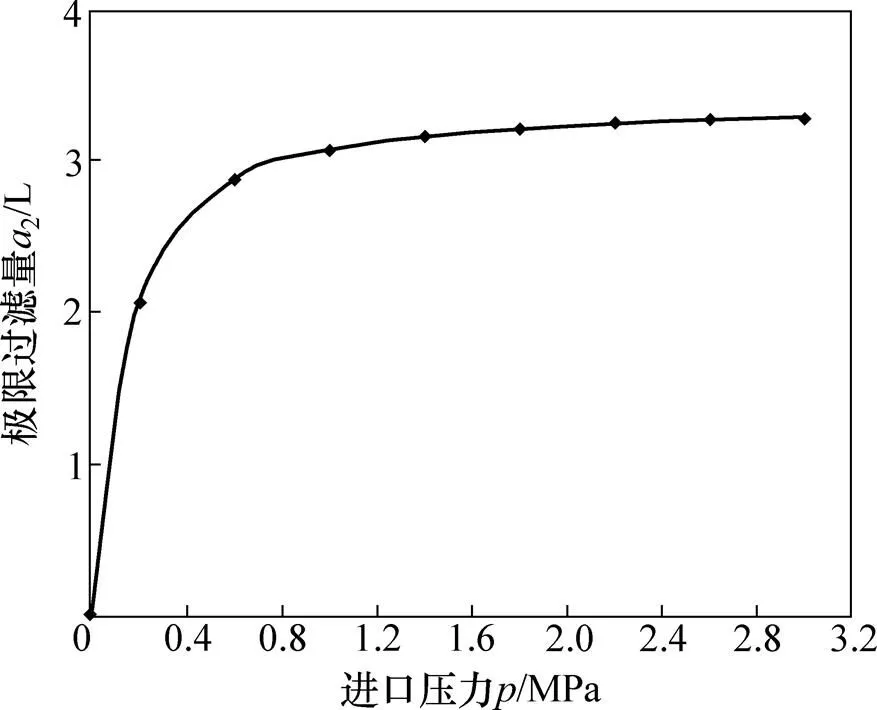
图5 压力p2与极限过滤量a2的关系

而参数2在一定污泥特性和压滤机工作参数下几乎不随过滤压力发生变化。

3.2.3 鼓膜阶段

假设以鼓膜阶段压力3继续进料压滤，其极限滤液量3=2(其中，为鼓膜极限滤液量与压滤极限滤液量比例系数)。但是鼓膜阶段停止进料，隔膜板以一定压力对泥饼压缩，通过减小滤室体积达到过滤目的，极限滤液量必然小于3，故3并不是鼓膜阶段的极限滤液量。本文称3为鼓膜阶段虚拟极限滤液量，3’为鼓膜阶段虚拟滤液量，其值只是数学意义上的假设，并不是真实的滤液量，如图6所示。

由于过滤面积没有发生变化，故鼓膜开始瞬时的比过滤速度仍满足32的关系。由式(4)近似认为有

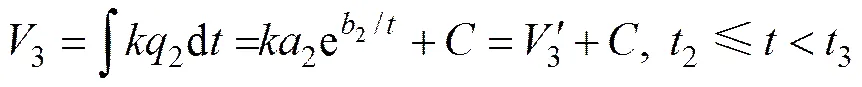
其中：为常数，表示压滤结束后以鼓膜压力继续进料所产生的滤液量。

若从2时刻停止压滤，则开始鼓膜。将2和2代入上式可得：

(5)

3.2.4 压滤机反吹、卸料及清洗准备阶段

鼓膜结束后，还需要进行反吹过程将管道内残留的泥浆和滤液清理干净。然后，进入卸料过程以及为下一周期工作的准备阶段。该阶段时间基本为定值。

3.2.5 压滤机工作阶段时间点的优化

如图1所示，非过滤总和时间010，压滤机过滤时间233，则压滤机的工作周期03，其中压滤时间2=2，鼓膜时间33−2。假设原污泥含水率为0，在3时，鼓膜过程泥饼最终含水率达到f，为污泥脱水标准。设进料总体积为，则有

(6)

将式(4)和(5)代入式(6)，有

在达到含水率f标准的前提下，可以通过数学模型优化2和3，求解压滤机最大生产效率max：

生产速率与压滤时间2的关系式为

(8)

式中：为总进料量；1为滤室体积；0为非过滤阶段总和时间；3为压滤机单周期工作时间；0为原污泥含水率；f为期望过滤总量；2为极限过滤量(a＞0)；2为压滤阶段过滤参数(2＜0)。

在实际生产中，由于鼓膜阶段隔膜的膨胀形变量并不是任意大，若泥饼没有达到一定厚度，则隔膜板的压力不能充分作用在泥饼上，这就限制了该方法计算最佳压滤时间的适用范围。

基于上述问题，应根据实际中隔膜压滤机隔膜板的隔膜膨胀性能，设定最小进料量min。当理论计算的压滤时间2对应的进料总量＞min时，通过上述方法所计算的2即为最佳压滤时间，3即为最佳鼓膜时间。当理论计算的压滤时间2对应的进料总量＜min时，达到min的时间2′即为最佳压滤时间。

4 污泥处理厂压滤机工作周期优化

4.1 压滤机工作参数

某污泥处理厂日处理含水率为95%的污泥 500 m3，设计采用4台XAGZ200/1250−30u型号隔膜压滤机同时24 h工作，实际不能完成工作任务。目前，该厂压滤机工作周期=210 min。其中准备时间为 20 min，进料时间为10 min，压滤时间为120 min，鼓膜时间为30 min，反吹时间为10 min，卸料时间为 20 min。

XAGZ200/1250−30u隔膜压滤机参数如下：面积为200 m2；滤室数为80个；滤板外径为1 250 mm× 1 250 mm；滤室厚度为30 mm；中心进料，额定过滤压力为0.8 MPa，额定压榨压力为1.6 MPa。记录压滤机工作过程滤液量，如表2所示。

表2 压滤阶段滤液总量与时间关系

压滤过程结束时，滤液总量为14.36 m3。鼓膜阶段结束时滤液总量为15.17 m3，最终泥饼含水率为60.4%。压滤机污泥处理速率=0.083 m3/min。

4.2 压滤机各工作阶段时间优化

首先用数学模型描述压滤阶段的V()−函数，用最小二乘法建立时间与压滤阶段过滤总量V()的经验公式。

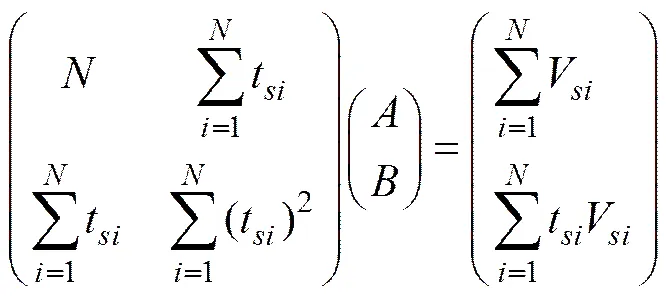
为使拟合精确，记录点个数要尽量多，求得=2.877，=−25.46。故得2=17.76，2=−25.46。

由于压滤阶段和鼓膜阶段的参数23，故3/23′/2(3(3))2(3)，解得=1.29。其他参数值为：滤室体积1=3 m3，非过滤时间总和01=60 min，滤饼最终含水率f=60.4%。压滤机工作速率方程参数如下：2为17.76，2为−25.46，0为95%，f为60.4%，0为60 min，为1.29，1为3 m3。将这些参数代入式(7)和式(8)，利用Matlab软件得到工作效率与压滤时间2的关系如图7所示。

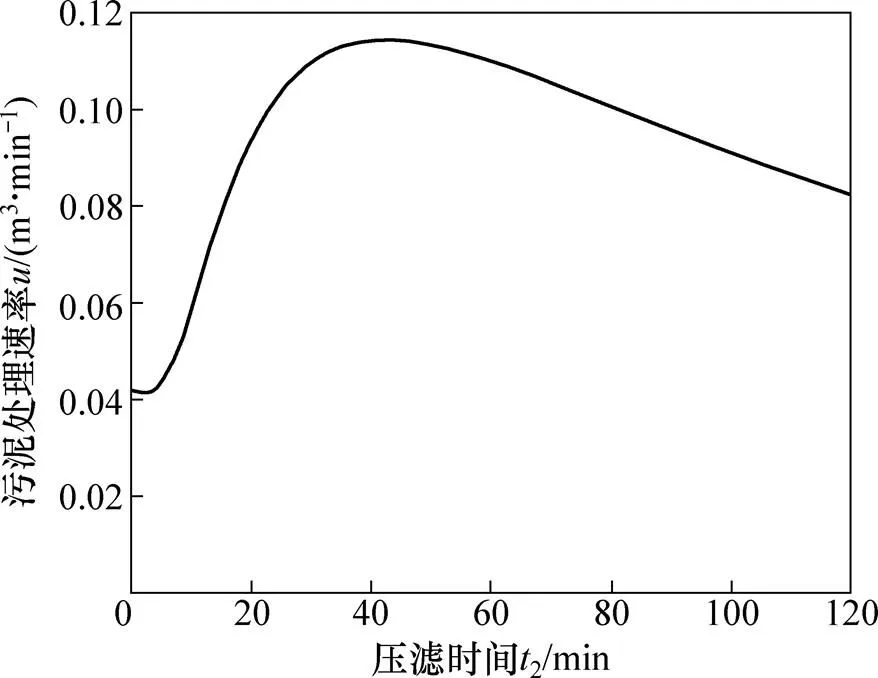
图7 工作效率u与压滤时间t2关的关系

求得：2=42.7 min，3=51.9 min。则压滤时间2=2=42.7 min，鼓膜时间3=3−2=9.2 min，处理污泥总量=17.36 m3，=0.1 143 m3/min。优化前后各参数比较见表3。

对压滤时间2和鼓膜时间3进行优化计算，该污泥处理厂单台压滤机污泥处理速率提高37.7%。

按照原压滤机工作流程时间设定，每台压滤机每天可工作6个周期，4台压滤机每天处理量约 416.64 m3，不能完成当日生产任务。优化后压滤机工作周期约2 h，每日作业12个周期，日产能力可达613.44 m3。该厂按本文提出的周期实际作业，在完成任务的同时，轮流让其中1台机休息待机，不但满足污泥处理厂的产量要求，而且可以使压滤机得到更多的停歇和检修时间，有利于延长压滤机的使用寿命。

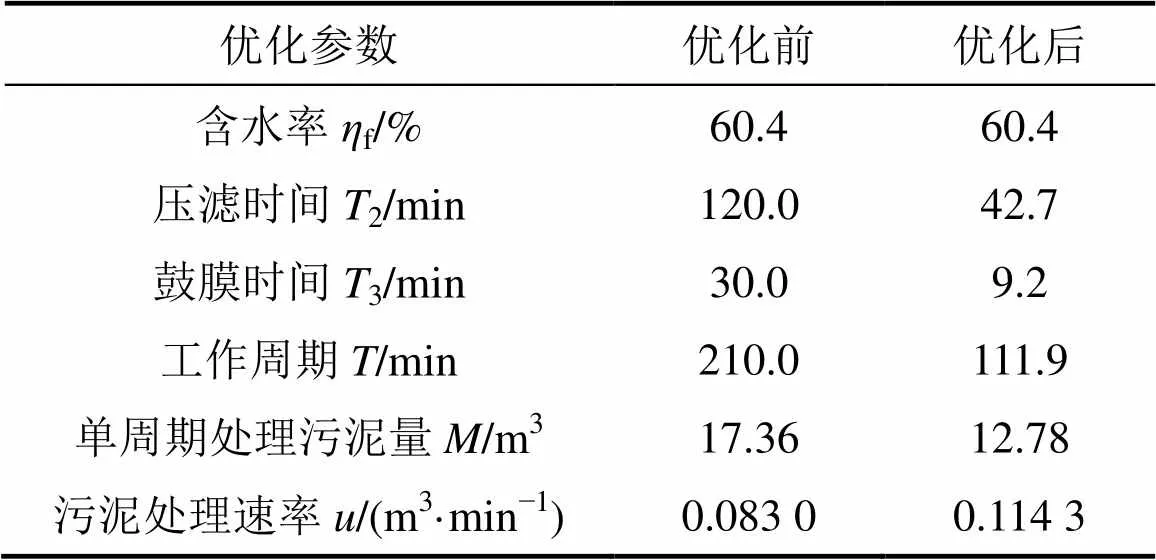
表3 优化前后各参数比较

5 结论

1) 基于Fluent模拟得到压滤机压滤阶段不同压力下滤液总量与时间的关系，运用最小二乘法拟合该曲线的函数表达式，得到滤液总量与压力的变化关系。

2) 提出了鼓膜阶段虚拟滤液总量3′的概念，即假设以鼓膜压力3继续进料，不改变滤室容积条件下的滤液总量。以此推导得到鼓膜阶段实际滤液总量3随时间变化的数学关系式，并得到压滤机工作效率与压滤时间t的数学关系式。

3) 对某污泥处理厂隔膜压滤机各工作阶段时间进行优化计算，其污泥处理效率提高37.7%。

[1] 邓玲. 厢式隔膜压滤机深度脱水性能研究[D]. 长沙: 中南大学机电工程学院, 2014: 1−35. DEND Ling. Filter characteristics research on deep dehydration of sludge in van membrane filter press[D]. Changsha: Central South University. School of Mechanical and Electrical Engineering, 2014: 1−35.

[2] 吴学伟. 基于两级也太调质理论的污泥处理处置技术[M]. 北京: 科学出版社, 2008: 34−36. WU Xuewei. Technology of sludge treatment and disposition[M]. Beijing: Science Press, 2008: 34−36.

[3] BENSAID S, MARCHISIO D L, FINO D. Numerical simulation of soot filtration and combustion within diesel particulate filters[J]. Chemical Engineering Science, 2010, 65(1): 357−363.

[4] 刘鹏, 刘国荣, 王国栋, 等. 过滤过程中滤饼比阻及其影响因素的研究[J]. 广东化工, 2009, 36(4): 28−30. LIU Peng, LIU Guorong, WANG Guodong, et al. Research on cake resistance and its influencing factors during cake filtration process[J]. Guangdong Chemical Industry, 2009, 36(4): 28−30.

[5] 赵扬, 许泽银, 谭蔚, 等. 压榨过滤过程中提前压榨技术的试验研究[J]. 合肥工业大学学报(自然科学版), 2010, 33(8): 1140−1144. ZHAO Yang, XU Zeyin, TAN Wei, et al. An experimental study of pre-press technology in the process of press filtration[J]. Journal of Hefei University of Technology (Natural Science), 2010, 33(8): 1140−1144.

[6] STICKLAND A D, DE KRETSER R G, SCALES P J, et al. Numerical modelling of fixed-cavity plate-and-frame filtration: formulation, validation and optimisation[J]. Chemical Engineering Science, 2006, 61(12): 3818−3829.

[7] 刘德忠, 王湛. 微滤膜过滤过程中比阻的研究进展[J]. 膜科学与技术, 2005, 25(5): 63−68. LIU Dezhong, WANG Zhan. Research progress of specific resistance during microfiltration process[J]. Membrane Science and Technology, 2005, 25(5): 63−68.

[8] 罗茜. 成饼过滤中过滤介质阻力与堵塞研究的进展[J]. 过滤与分离, 2007, 17(3): 37−45. LUO Qian. Progress in study on the resistance of filter media and its clogging in cake filtration[J]. Journal of Filtration & Separation, 2007, 17(3): 37−45.

[9] 许莉, 李文革, 鲁淑群, 等. 过滤理论与滤饼结构的研究[J]. 流体机械, 2000, 28(10): 10−13. XU Li, LI Wenge, LU Shuqun. Proceedings of filtration theory and studies in filtration cake structure[J]. Fluid Machinery, 2000, 28(10): 10−13.

[10] 谢小青, 黄珍艺, 戴兰华, 等. 厦门城市污泥深度脱水处理及资源化利用研究[J]. 中国给排水, 2010, 26(5): 138−140. XIE Xiaoqing, HUANG Zhenyi, DAI Lanhua, et al. Study on deep dewatering and recycling of municipal sludge in Xiamen[J]. China Water & Wastewater, 2010, 26(5): 138−140.

[11] 赵培涛, 葛仕福, 黄瑛, 等. 压滤式污泥过滤比阻测定方法[J]. 东南大学学报(自然科学版), 2011, 41(1): 155−159. ZHAO Peitao, GE Shifu, HUANG Ying, et al. Measurement of specific resistance to filtration of sludge by pressure filtration[J]. Journal of Southeast University (Natural Science Edition), 2011, 41(1): 155−159.

[12] 姜立新, 罗茜, 赵松年, 等. 压榨脱水的试验研究[J]. 过滤与分离, 2003, 13(1): 14−18. JIANG Lixin, LUO Xi, ZHAO Songnian, et al. Experimental study on the squeeze dewatering[J]. Journal of Filtration & Separation, 2003, 13(1): 14−18.

[13] 王雪伟, 张文军, 胡格伟, 等. 煤泥离心过滤和机械压滤的滤饼层粒度分布及其影响[J]. 煤炭学报, 2014, 39(10): 2087−2091. WANG Xuewei, ZHANG Wenjun, HU Gewei, et al. Particle size distribution of fine coal cake in filtering centrifuge and press filter and its influences on specific filtering resistance[J]. Journal of China Coal Society, 2014, 39(10): 2087−2091.

[14] 祝贵兵, 王淑莹, 李探微, 等. 采用污泥过滤进行固液分离的试验研究[J]. 哈尔滨工业大学学报, 2004, 36(6): 739−742, 772. ZHU Guibing, WANG Shuying, LI Tanwei, et al. Separation of solid and liquid by sludge filtration[J]. Journal of Harbin Institute of Technology, 2004, 36(6): 739−742, 772.

(编辑 陈灿华)

Optimization and research of membrane filter press procedure on dehydration of sludge

ZHU Guihua, GAO Mingquan, MA Kai, TANG Xiao, ZHU Tianhong, XU Hongwei

(School of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China)

In order to study filterability of membrane filter press in each work stage, the filter processes were simulated to find the regulation between the filter volume and the work time by software Fluent. And the algorithm was fitted by the least square method. According to the simulation results, a conception named virtual filter volume that can describe the regulation between the filter volume and work time in the stage of inflating membrane was put forward by mathematical method. Then the efficiency formula of filter press was derived. The results show that pressure filter time is the key factor to the efficiency formula of filter press, and the work efficiency of a certain sludge treatment plant is increased by 37.7% using this mathematical method. The optimum work cycle time of filter press is obtained, and its work efficiency is improved greatly.

membrane filter press; the least square method; optimal filtering time; specific filter velocity

10.11817/j.issn.1672−7207.2017.02.003

X703.3

A

1672−7207(2017)02−0289−06

2016−02−10；

2016−04−22

湖南省科技计划重点项目(2014SK2020)(Project(2014SK2020) supported by the Key Project of Science and Technology of Hunan Province)

朱桂华，博士研究生，副教授，硕士生导师，从事环保装备研究；E-mail：zhuguihuaok@163.com