修形圆柱齿轮啮合刚度计算公式

唐进元，蔡卫星，王志伟



修形圆柱齿轮啮合刚度计算公式

唐进元，蔡卫星，王志伟

(中南大学高性能复杂制造国家重点实验室，湖南长沙，410083)

基于CAD/CAE工具与方法，提出一种基于有限元软件定量计算修形齿轮啮合刚度、重合度等性能参数的计算方法，通过数值计算结果阐明修形齿轮修形量与啮合刚度等等定量关联规律。基于有限元准静态分析和齿轮啮合刚度计算原理给出修形齿轮啮合刚度计算公式，解决修形齿轮动力学研究中的刚度计算问题，给出微米级齿轮修形参数对轮齿啮合刚度的影响规律。研究结果表明：利用该计算方法所得结果与FE软件计算结果相吻合，为科学、合理地选择与评价齿轮修形参数提供一种解决方法，为高性能齿轮设计提供参考。

齿轮；修形；有限元；啮合刚度

齿轮修形对改善齿轮传动的啮合性能特别是动力学性能有重要作用[1−5]。其中，IMREK等[6−10]理论和试验角度对直齿轮、斜齿轮等进行了分析，LITVIN等[11]给出了齿轮修行的几何分析方法；吴勇军等[12−14]从理论分析的角度给出了轮齿修形的基本理论以及设计方法。尽管人们对普通渐开线圆柱齿轮的修形进行了大量研究，一些较好的商用齿轮传动设计分析软件中也有相关的分析设计功能，但对齿轮修形的研究还是有必要：1) 修形参数(修形起始点位置与齿顶修形量)与齿轮传动的啮合刚度、重合度等性能参数的定量关联公式对修形齿轮动力学非常重要，目前还没有相应的计算公式；2) 设计手册[1−2]中给出的修形量范围大，针对具体工况的精确设计缺乏理论指导与技术方法；3) 一些国外商用齿轮传动设计分析软件中的分析设计功能定量计算模型是商业秘密，中国作为齿轮大国，很有必要掌握其设计原理。啮合刚度等参数与传动性能密切相关，微米量级的修形量对轮齿的弯曲变形几乎没有影响，而对沿着接触轨迹的时变啮合刚度有较大影响。为此，本文作者基于CAD/CAE工具与方法，提出一种基于有限元软件定量计算修形齿轮啮合刚度、重合度等性能参数的计算方法，通过数值计算结果阐明修形齿轮修形量与修形齿轮传动性能参数的关联规律。

1 修形齿轮啮合刚度有限元计算 方法

1.1 修形齿轮几何模型建模

为得到精确的齿轮有限元分析模型，基于已有齿轮虚拟加工制造研究成果[15]和修形齿轮刀具设计方法[14]，用CATIA软件进行齿轮三维几何建模。齿轮传动参数如下：小轮齿数为25个；大轮齿数为33个；模数为4 mm；压力角为25°；齿顶高系数为1；顶隙系数为0.25；齿宽为28 mm。设齿条刀具无凸台、过渡曲线由刀具圆角部分切出，圆角半径为1.2 mm。根据该齿轮几何参数，通过CATIA软件的二次开发、虚拟加工离散运算对毛坯进行切削处理，然后提取切削的刀痕线并拟合成齿面，从而生成几何模型，如图1所示。

图1 齿轮3D几何模型

1.2 修形齿轮修形参数设置

工程中齿轮修形主要有鼓形修形和齿高修形2种形式，齿高修形如图2所示。齿高修形可以有效降低轮齿的啮入、啮出冲击，有效改善齿轮系统的传动性能，在实际工程中应用广泛。

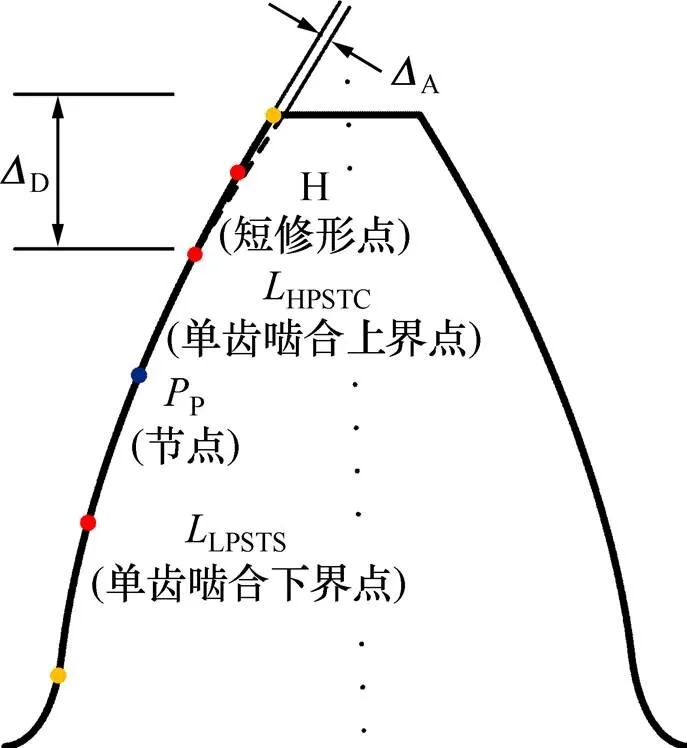
图2 齿轮齿高修形示意图

齿高修形参数主要包含齿顶修形量A、修形起始点位置D(即修形起点到齿顶的径向距离，一般采用修形起始点的滚动角表达)及修形曲线形式3个参数。对于齿顶修形量A，目前依然没有统一的计算公式，各国的计算标准也不同。齿顶修形量的计算方法主要分为2类：1) 按照轮齿受载变形确定齿顶修形量； 2) 按照制造精度来确定齿廓齿顶修形量。在文献[1−2]中，按压力角不同，齿顶修形量推荐取(0.325~0.400)(其中为模数)。基于文献[1−2]，齿顶修形量的取值如表1所示。修形曲线方程通常采用下列表达形式：

其中：A为齿顶修形量；为啮合线方向度量的修形长度；为以啮合线上修形起点为坐标原点在啮合线上任意位置的坐标。当取1时，齿廓修形方式为直线修形。本文中齿轮采用直线修形。为研究不同修形高度对齿轮系统传动性能的影响，选取3个具有代表性的修形起始点位置，分别对应齿轮的短修形点和单齿啮合上界点HPSTC，即齿轮的长修形点和齿轮的单齿啮合下界点LPSTC。

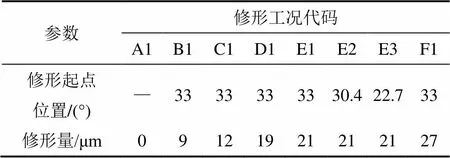
表1 齿轮修形参数

1.3 齿轮啮合刚度及传动误差有限元计算原理

基于作者前期工作[16−18]，可以推广得到修形齿轮啮合刚度与传动误差有限元数值计算方法，其计算原理如下。

在有限元准静态分析中，齿轮副啮合刚度与转矩的关系可表示为[19]

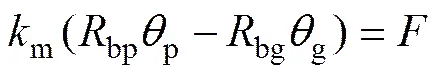
其中：p和g分别为有限单元方法得到的主动轮和被动轮的转动角度；bp和bg分别为主、被动齿轮的基圆半径；为法向啮合力；m为齿轮啮合刚度。

当齿轮不存在误差时，根据式(2)可以得到齿轮啮合刚度。但是面误差或者轮齿修形会改变齿轮的啮合历程，引起无负载传动误差(LTE)。无负载传动误差导致齿轮啮合过程产生刚性位移，在计算轮齿受载变形时必须减去。无负载传动误差(LTE)可以通过在有限元模型中对主动轮添加一微小载荷计算得到主动轮、被动轮转角，通过式(2)得到。因此，受载作用下修形齿轮的传动误差计算公式为[18−19]

则基于有限单元方法的修形齿轮啮合刚度计算式可以表示为

(4)

2 载荷对刚度的影响

根据前面给出的齿轮啮合刚度有限元计算方法，探讨载荷对齿轮啮合刚度的影响。图3所示为不同载荷状况下的齿轮啮合刚度。

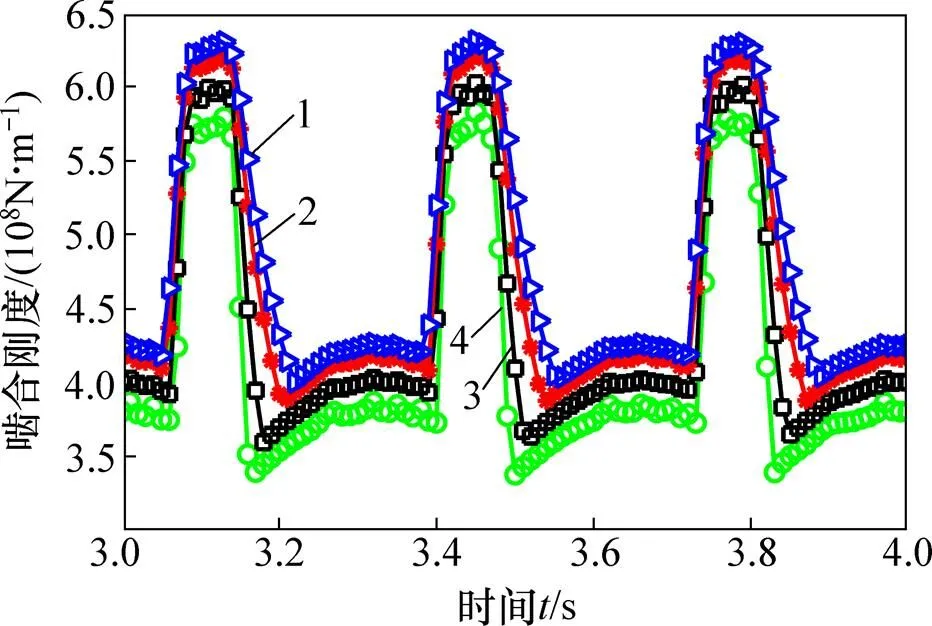
荷载/(N·m)：1—100.0；2—200.0；3—358.7；4—473.8。

从图3可以看出：在不同载荷下，啮合刚度曲线不同，主要表现为载荷增大，啮合刚度相应峰峰值和平均值增大，整条刚度曲线位于小载荷刚度曲线上方。图4所示为不同载荷下齿轮节点处的刚度。

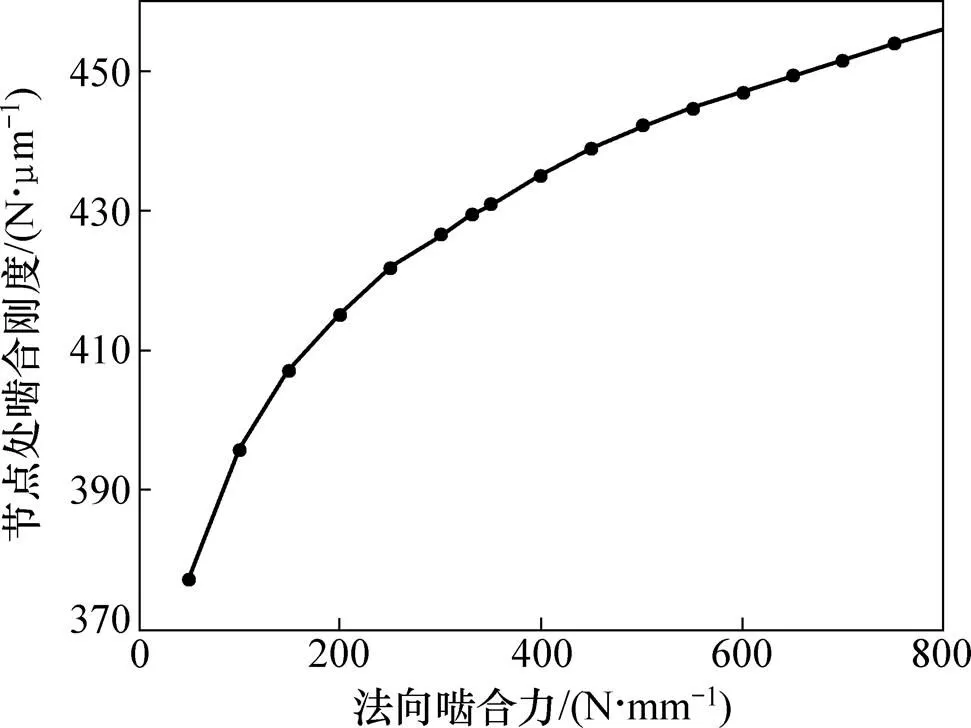
图4 不同载荷下齿轮节点处的啮合刚度

从图4可以看出：节点处的刚度与载荷呈非线性关系。而研究者大多没有考虑载荷对齿轮刚度的影 响[20]。双齿区的一对轮齿承担的载荷远小于单齿区轮齿对承担的载荷，因此，在计算双齿区刚度时，若不考虑这影响显然会造成较大误差。在ISO双齿区刚度计算公式中，双齿区刚度并非单齿区刚度单纯相加，这样，通过对文献[20]中刚度计算公式引入载荷系数()，可以得到更准确的计算结果。

式中：为单位齿宽上法向啮合力，kN/mm。由此可得到单齿啮合刚度计算公式为：

(6)

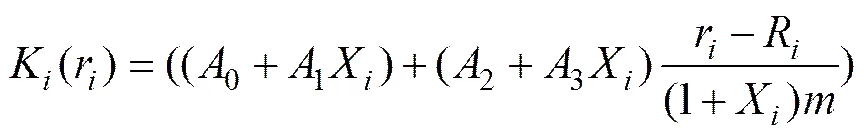
其中：

双齿啮合刚度计算公式为

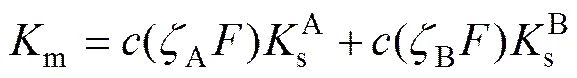
其中：A和B为啮合轮齿载荷分配率，具体为每个轮齿上承担载荷占齿轮所传递总载荷的比值。为了简化，均取0.5；和为2对啮合轮齿的啮合刚度；z和X分别为齿轮的齿数和变位系数。

计算式改进前后的计算结果、有限元计算结果和ISO6336:2006中的结果对比如图5和表2所示。从图5和表2可以看出：本文改进后计算结果显然更接近ISO和有限元计算结果，且双齿区啮合刚度按原公式所得结果明显偏大，这是由于原计算方法没有考虑载荷对啮合刚度的影响而引起的误差。从图5可知：载荷对刚度的影响较明显，不能够忽略载荷对刚度的影响。表2中平均刚度是齿轮1个啮合周期刚度的平均值。

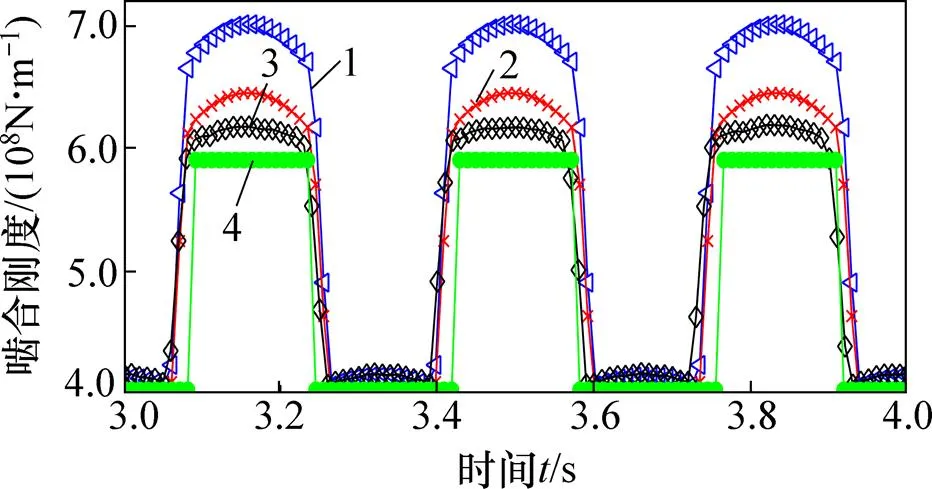
方法：1—原公式；2—改进公式；3—有限元法；4—ISO 6336。

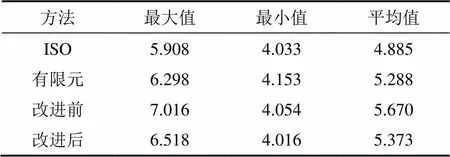
表2 3种刚度计算方法计算结果对比

3 齿廓修形参数对啮合刚度的影响

图6所示为修形齿轮啮出示意图。从图6可知：修形齿轮的基节长度b变小，减少量就是该位置时齿廓的法向修形量；当齿轮副进行啮合传动时，由于主动轮基节变小，参与啮合的2个轮齿是先后进入啮合的，轮齿1先进入啮合；当啮合齿对1在啮合线上发生变形等于轮齿2修形量时，轮齿2进入啮合参与传动。根据上述轮齿啮合过程，可以推导得到修形齿轮啮出时的刚度计算式：

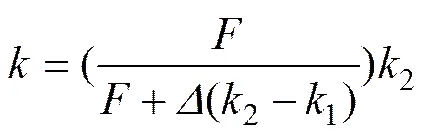
式中：为额定载荷时法向啮合力；1和2分别为啮合位置处齿轮的单、双齿啮合刚度。显然，式(9)是齿廓修形量的递减函数。根据式(9)和采用有限元方法得到的修形齿轮与有限元计算结果对比如图7所示。根据式所得计算结果与有限元计算结果基本一致(见表3)，特别是在修形区域刚度的计算上，两者具有很高的一致性，且两者的计算相对误差都在3%左右，平均啮合刚度的相对误差低于1%，这说明上述计算公式具有较高的准确度。

图6 齿轮啮出示意图

Fig. 6 Illustration of modification gear meshing

方法：1—解析公式；2—有限元法。

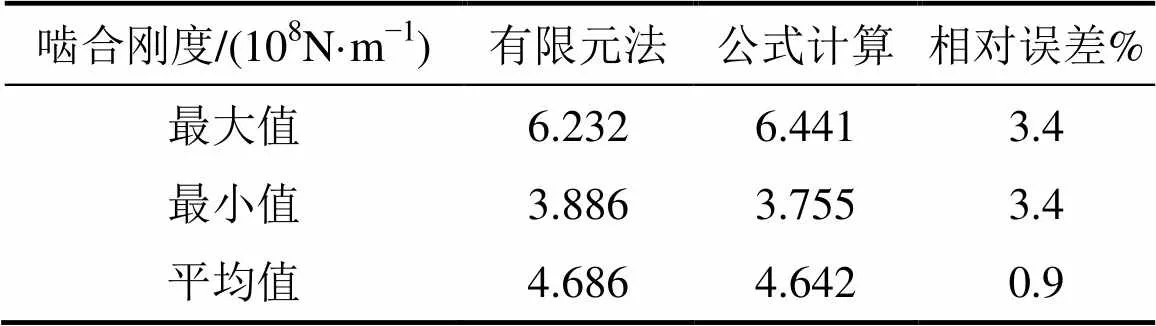
表3 修形计算结果对比

3.1 修形起始点位置对刚度的影响

取齿顶修形量A=21 μm，并在大轮上施加扭矩473.8 N·m，研究修形起始点位置对啮合刚度的影响，计算得到的齿轮啮合刚度如8所示。

从图8可见：无修形时(图8中曲线1)，单双齿交替时齿轮啮合刚度变化较陡峭，重合度为1.647；修形位置在(33°)点时(图8中曲线2)，在单齿啮合区内齿轮啮合刚度变化较小，轮齿啮出时较平稳，齿轮啮出刚度变化也比较平缓，重合度为1.515；当修形起始点位置增加至HPSTC(30.4°)点时(图8中曲线3)，单齿区的长度稍微变大，轮齿啮出时刚度变大，重合度为1.471；当修形位置在LPSTC(22.7°)时(图 8中曲线4)，修形对单齿区及双齿区具有比较大的影响，单齿区增大，在啮入点附近有比较短的双齿啮合区，齿轮啮合刚度变成1个尖峰，平均齿轮啮合刚度降低比较明显，重合度变为1.088。从以上结果可以看出：在一定修形量下，修形起始点位置越大，其相应重合度越小，刚度曲线变化越大，也更复杂。

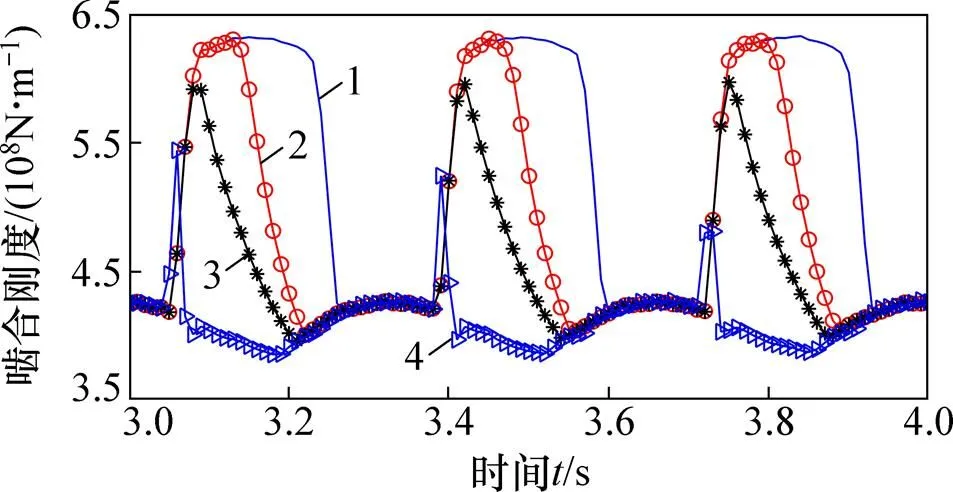
工况：1—A1；2—E1；3—E2；4—E3。

3.2 齿顶修形量对啮合刚度的影响

设修形位置都在(33°)点，在大轮上施加473.8 N·m的扭矩，得到不同齿顶修形量时轮齿的啮合刚度如图9所示。

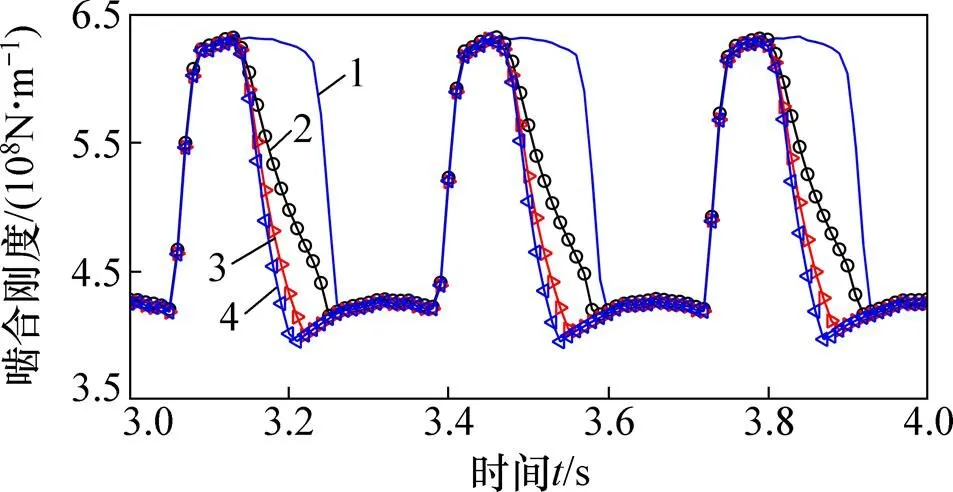
工况：1—A1；2—C1；3—E1；4—F1。

从图9可见：轮齿的啮合刚度的峰值并没有随着齿顶修形量的改变而发生明显变化，并且随着齿顶修形量增大，轮齿啮合刚度在啮入时变化并不明显，但在啮出区域，其刚度的变化越来越大；同时，随着齿顶修形量增大，齿轮的单齿啮合区域变大，双齿啮合区域变小，A1工况时的重合度为1.647，C1工况时的重合度为1.617，E1工况时的重合度为1.515，F1工况时的重合度为1.471，即重合度随着齿顶修形量的增大而减小。因此，齿轮齿顶修形虽然可以降低啮入啮出冲击，但齿顶修形量不宜选取过大，修形量可在单齿啮合最高点的变形量附近选取。过大的修形量会降低齿轮重合度而影响齿轮传动的平稳性，修形量推荐选取为单齿啮合最高点的轮齿啮合变形量。

4 结论

1) 给出修形齿轮啮合刚度有限元计算方法与解析计算公式，解决了修形齿轮啮合刚度、传动误差、重合度等性能参数计算问题，为修形齿轮的科学设计提供了一种技术方法。

2) 在齿轮修形方式中，齿廓修形会较大程度地改变刚度曲线的形状，对峰峰值影响较小，而鼓形修形会引起刚度峰峰值与平均值的改变，但对刚度曲线形状影响不大。

3) 在载荷与修形起始点位置不变的条件下，随着齿顶修形量增大，重合度减少，齿轮的啮合刚度变小，刚度平均值明显降低，但其峰峰值变化不大。齿顶修形量的选择尽量在主动轮单齿啮合最高点即轮齿啮合变形量附近。

4) 当载荷与修形量不变时，随着齿顶修形起始点位置增大，重合度减小，平均值减小，齿顶修形起始点位置不能超过单齿啮合上界点，否则，啮合刚度曲线发生畸变，严重影响传动性能。

5) 当修形起始点位置、齿顶修形量一定时，随着载荷增加，啮合刚度增大，重合度增大。同时，载荷对刚度影响是非线性的，根据单齿刚度计算双齿区刚度时需考虑载荷对刚度的影响。

[1] 齿轮手册编委会.齿轮手册(上册)[M]. 2版. 北京: 机械工业出版社, 2004: 143−150. Handbook of Gear Committee. Handbook of gear(I)[M]. 2nd ed. Beijing: China Machine Press, 2004: 143−150.

[2] STEPHEN P. Radzevich, Dudley’s handbook of practical gear design and manufacture[M]. 2nd ed. CRC Press Inc, 2012.

[3] LIU Jiahung, CHANG Shinnliang. Research on gear plunge shaving for gears with tooth modifications[C]//Proceedings of the International Multiconference of Engineers and Computer Scientists. Hong Kong, China, 2009: 18−20.

[4] HSI LIN H, OSWALD F B, TOWNSEND D P. Dynamic loading of spur gears with linear or parabolic tooth profile modifications[J]. Mechanism and Machine Theory, 1994, 29(8): 1115−1129.

[5] UMEZAWA K. The performance diagrams for the vibration of helical gears[C]//Proceedings of the 1989 International Power Transmission and Gearing Conference. Chicago, 1989: 399−408.

[6] IMREK H, DUZCUKOGLU H. Relation between wear and tooth width modification in spur gears[J]. Wear, 2007, 262(3): 390−394.

[7] LIN H H, TOWNSEND D P, OSWALD F B. Profile modification to minimize spur gear dynamic loading[R]. National Technical Information Service, SPRINGFIELD, VA(USA), 1987.

[8] CAI Y, HAYASHI T. The optimum modification of tooth profile for a pair of spur gears to make its rotational vibration equal zero[C]//Advancing Power Transmission into the 21st Century, 1992: 453−460.

[9] MAATAR M, VELEX P. Quasi-static and dynamic analysis of narrow-faced helical gears with profile and lead modifications[J]. Journal of Mechanical Design, 1997, 119(4): 474−480.

[10] KAHRAMAN A, BLANKENSHIP G. Effect of involute tip relief on dynamic response of spur gear pairs[J]. Transactions-American Society of Mechanical Engineers Journal of Mechanical Design, 1999, 121(7): 313−314.

[11] LITVIN F L, FUENTES A. Gear geometry and applied theory[M]. Cambridge: Cambridge University Press, 2004: 404−440.

[12] 吴勇军, 王建军, 韩勤锴, 等.基于接触有限元分析的斜齿轮齿廓修形与实验[J]. 航空动力学报, 2011, 26(2): 409−415.WU Yongjun, WANG Jianjun, HAN Qinkai, et al. Tooth profile modification of helical gears and experimental study based on finite element contact analysis[J]. Journal of Aerospace Power, 2011, 26(2): 409−415.

[13] 王朝晋, 丁玉成.关于齿廓修形的研究(二)[J]. 齿轮, 1986, 10(3): 8−11. WANG Chaojin, DING Yuchen. The study of profile modification(two)[J]. Gear, 1986, 10(3): 8−11.

[14] 李润方.齿轮传动的刚度分析和修形方法[M]. 重庆: 重庆大学出版社, 1998: 140−286. LI Runfang. The stiffness analysis and modification method of gear transmission system[M]. Chongqing: Chongqing University Press, 1998: 140−286.

[15] 唐进元, 肖利民. 对YM7132A修缘样板设计公式的补充[J]. 制造技术与机床, 1996(4): 19−21. TANG Jinyuan, XIAO Limin. The supplement to the YM7132A formula[J]. Manufacture Technology and Machine Tools, 1996(4): 19−21.

[16] 蒲太平, 唐进元.基于 CATIA V5 的圆柱齿轮虚拟加工研究[J]. 系统仿真学报, 2008, 20(16): 4339−4343. PU Taiping, TANG Jinyuan. Virtual machining process research of spur-gear based on CATIA V5[J]. Journal of System Simulation, 2008, 20(16): 4339−4343.

[17] 唐进元, 王志伟, 伊洪丽, 等. 齿根裂纹与轮齿啮合刚度关联规律研究[J]. 机械传动, 2014, 38(2): 1−4. TANG Jinyuan, WANG Zhiwei, YI Hongli, et al. Study on the association rule of root crack and gear mesh stiffness[J]. Journal of Mechanical Transmission, 2014, 38(2): 1−4.

[18] 唐进元, 王志伟, 雷敦财. 载荷与齿轮啮合刚度、重合度的关系研究[J]. 机械传动, 2014, 38(6): 1−4. TANG Jinyuan, WANG Zhiwei, LEI Duncai. Study on the relationship between load and gear mesh stiffness,contact ratio[J]. Journal of Mechanical Transmission, 2014, 38(6): 1−4.

[19] 雷顿财, 唐进元. 一种面齿轮传动时变啮合刚度数值计算方法[J]. 中国机械工程, 2014, 25(17): 2300−2304. LEI Duncai, TANG Jinyuan. A numerical calculation method of face gear time-varying meshing stiffness[J]. Chinese Journal of Mechanical Engineering, 2014, 25(17): 2300−2304.

[20] VELEX P, AJMI M. On the modelling of excitations in geared systems by transmission errors[J]. Journal of Sound and Vibration, 2006, 290(3): 882−909.

[21] KUANG J, YANG Y. An estimate of mesh stiffness and load sharing ratio of a spur gear pair[J]. Advancing Power Transmission into the 21st Century, 1992, 2(7): 1−9.

(编辑 陈灿华)

Meshing stiffness formula of modification gear

TANG Jinyuan, CAI Weixin, WANG Zhiwei

(State Key Laboratory of High Performance Complex Manufacturing, Central South University, Changsha 410083, China)

The contact ratio and meshing stiffness of the tooth of modification gear were studied. A three-dimensional model of the modification gear was established based on the parameters of the modification including gear addendum amount of modification, modification length and repair-shaped curve. Through the finite element quasi-static analysis principle, the gear meshing stiffness calculation method was proposed based on the finite element numerical calculation. The relationship between the modification parameters (addendum amount, modification length, load) and the mesh stiffness of the modification gear was given. The results show that the calculation results obtained by the proposed method are consistent well with the calculation results obtained by FE software. The gear mesh stiffness calculation method provides a technical way to get the mesh stiffness of gear considering error and the amount of modification.

gear; modification; the finite element; mesh stiffness

10.11817/j.issn.1672−7207.2017.02.010

TH132.41

A

1672−7207(2017)02−0337−06

2016−02−08；

2016−04−09

国家自然科学基金资助项目(51535012，U1604255)；湖南省重点研发计划项目(2016JC2001)(Projects(51535012, U1604255) supported by the National Natural Science Foundation of China; Project(2016JC2001) supported by the Key Research and Development Plan of Hunan Province)

唐进元，教授，从事复杂曲面零件设计与制造研究；E-mail：jytangcsu@163.com