苗盘横向传动机构动力学分析探究
2017-03-16李树峰曹卫彬唐海洋赵宏政刘娇娣
李树峰,曹卫彬,唐海洋,赵宏政,刘娇娣,李 华
(石河子大学 机械电气工程学院,新疆 石河子 832003)
苗盘横向传动机构动力学分析探究
李树峰,曹卫彬,唐海洋,赵宏政,刘娇娣,李 华
(石河子大学 机械电气工程学院,新疆 石河子 832003)
曲柄摇杆与双摇杆齿轮组合机构具有结构简单、工作可靠等特点,可实现苗盘横向的精确传动,在苗盘输送机构中运用较多。但由于曲柄摇杆具有急回特性及机构做反复式运动必然产生振动和惯性力,影响机构运动平稳性,限制了机构工作效率。为此,针对一种应用于旱地移栽机苗盘横向输送传动机构——曲柄摇杆-双摇杆-齿轮传动机构,建立了机构的动力学模型,分析了曲柄、连杆、摇杆及齿轮之间的连接点与啮合点等处的受力随曲柄转角变化的规律。应用ADAMS软件完成了机构的虚拟样机模型建立,分析了机构作业过程中的动力学特征。利用上述方法找到了机构振动的原因,并提出解决减小振动方法,为苗盘传动机构的改进和进一步优化设计提供了理论依据。
移栽机;苗盘输送机构;动力学;ADAMS
0 引言
苗盘输送机构是钵苗自动移栽机的核心工作部件,决定着移栽的效率[1-2]。目前,国内推广使用移栽机为人工投苗的半自动移栽机,靠人工拾取苗盘进行投苗,长时间重复动作导致精神高度紧张、眼睛容易疲劳、劳动强度大,且人工换苗盘时容易出现漏苗、缺苗现象。由于受到人工投苗速度的限制,一般国内移栽机作业效率只相当于人工的5~15倍,而且1台2行移栽机作业需要司机1名、2名人员投苗及1~2名辅助人员跟踪补苗、覆土,增加了移栽成本,因此机械化作业综合效益不明显。为此,本文提出了一种自动送苗装置,只需要1名人员把苗盘放在苗盘架上和收取移栽完的苗盘,降低了劳动强度,减少了人工投入,提高了作业效率,为实现自动移栽机提出了参考。
1 基本结构及工作原理
苗盘横向进给机构三维模型如图1所示。本文所提出的传动装置由曲柄摇杆机构、双摇杆机构及齿轮机构组成。当变速箱通过锥齿轮把动力分配给曲柄,曲柄带动连杆作用于扇形摆块,摆块通过连杆作用于摇杆,摇杆通过齿轮轴驱动大齿轮转动1/4圈,齿轮螺母转动1周;丝杠带动苗盘横向运动30mm,使下一颗苗进入取苗工位。苗盘在横向进给的过程中存在着间歇运动,图2为间歇传动机构的装配三维图。其中,齿轮轴通过花键连接把动力传递给圆柱凸轮,端面加工有圆柱凸轮的齿轮的间歇运动由楔形圆柱凸轮和弹簧来控制。当齿轮轴逆时针旋转时,齿轮轴带动楔形圆柱凸轮沿着相啮合齿轮的楔形圆柱凸轮面从最低点向最高点滑动,由于两个圆柱凸轮楔形面的相互滑动,切断动力的传递,端面加工有圆柱凸轮的齿轮静止。当滑过楔形面的最高点时,楔形圆柱凸轮在弹簧作用力下复位重新啮合。此时,摇杆驱动齿轮轴顺时针旋转,齿轮轴通过花键连接的楔形圆柱凸轮驱动端面加工有圆柱凸轮的齿轮转动1/4圈,与其相啮合的齿轮螺母驱动丝杠横向移动30mm,完成一次横向送苗作业。

1.曲柄 2 长连杆 3.苗盘横向进给丝杠 4.卡槽齿轮 5.卡槽齿轮驱动摇杆 6.短连杆 7.扇形摆块 8.齿轮螺母图1 苗盘横向传动装置Fig.1 Horizontal transmission of the seedling tray
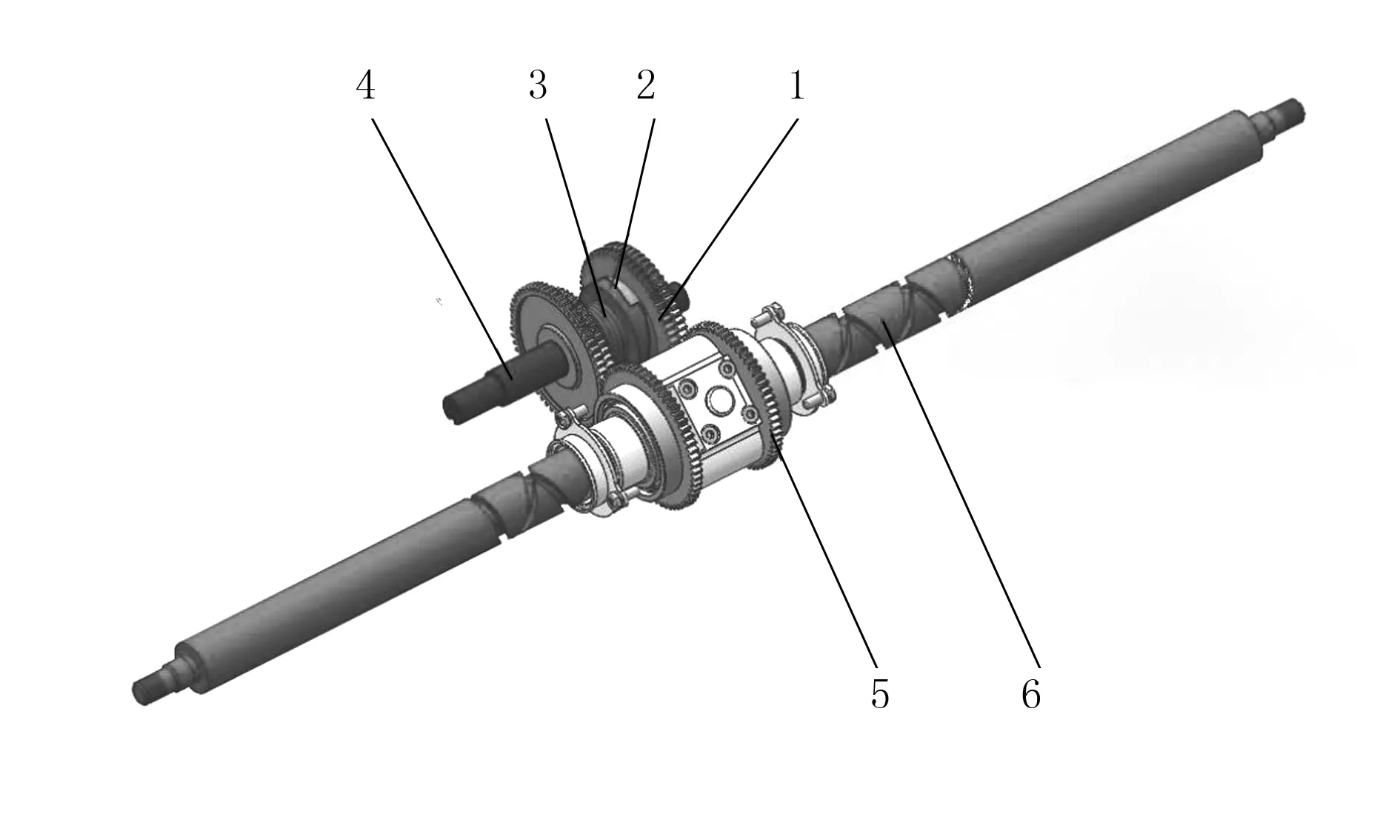
1.卡槽齿轮 2.圆柱凸轮 3.弹簧 4.齿轮轴 5.齿轮螺母 6.苗盘横向进给丝杠图2 间歇机构装配图Fig.2 Assembly drawing of intermittent mechanism
2 苗盘横向输送机构动力学模型
苗盘横向输送机构简化为曲柄摇杆机构、双摇杆机构和齿轮机构,如图3所示。其中,OA为曲柄,AB为连杆,BC为摇杆,DC为摇杆,DE为连杆,EF为摇杆,分别以F、G为圆心相互啮合的齿轮。
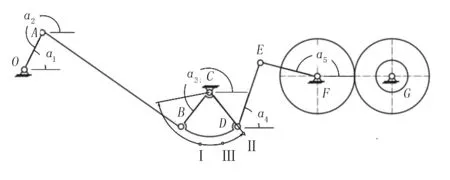
图3 机构示意图Fig.3 diagram of mechanism
2.1 曲柄OA受力分析
曲柄OA受力分析如图4所示。
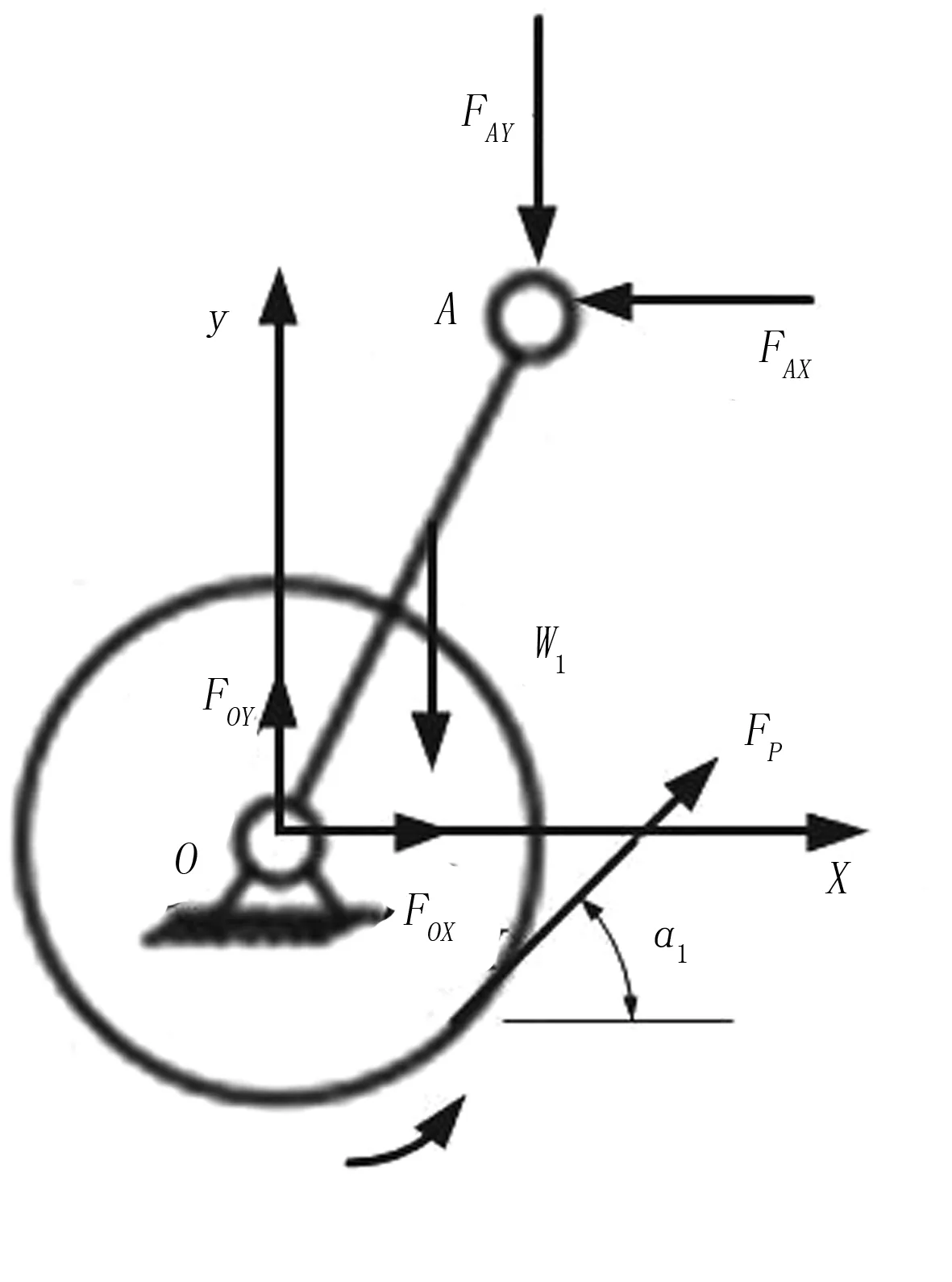
图 4 曲柄OA受力分析Fig.4 Force analysis of crank OA
根据图4分析曲柄OA受力情况,建立动力学平衡方程为
(1)
(2)
∑MO=FPR-FAYxA+FAXyA-W1x1=0
(3)
式中m1—曲柄OA的质量;
Fp—链轮所受拉力;
W1—曲柄OA所受重力;
x1—曲柄OAx轴质心;
y1—曲柄OAy轴质心。
2.2 连杆AB受力分析
连杆AB受力分析如图5所示。

图5 连杆AB受力分析Fig.5 Force analysis of connecting rod AB
根据图5分析连杆AB受力情况,建立动力学平衡方程为
∑Fx=FAX-FBNcos(α3-π)+
(4)
∑Fy=FAY+FBNsin(α3-π)+
(5)
∑MA=-FBNL2sin(α3-α2)-FBTL2cos(α3-α2)-
(6)
式中m2—连杆AB的质量;
W2—连杆AB所受重力;
x2—连杆ABx轴质心;
y2—连杆ABy轴质心。
2.3 扇形摆块受力分析
扇形摆块受力分析如图6所示。根据图6扇形摆块受力情况,建立动力学平衡方程为
(7)

(8)
∑MC=FBTL3sin(α3-α2)+W3(x3-x4)-
(9)
式中m3—扇形摆块的质量;
W3—扇形摆块所受重力;
x3—扇形摆块x轴质心;
y3—连杆ABy轴质心;
φ—扇形摆块的圆心角。
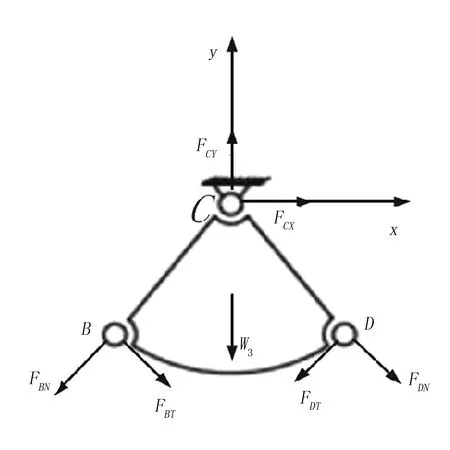
图 6 扇形摆块受力分析Fig.6 Force analysis of Fan-shaped swing block
2.4DE连杆受力分析
DE连杆受力分析如图7所示。
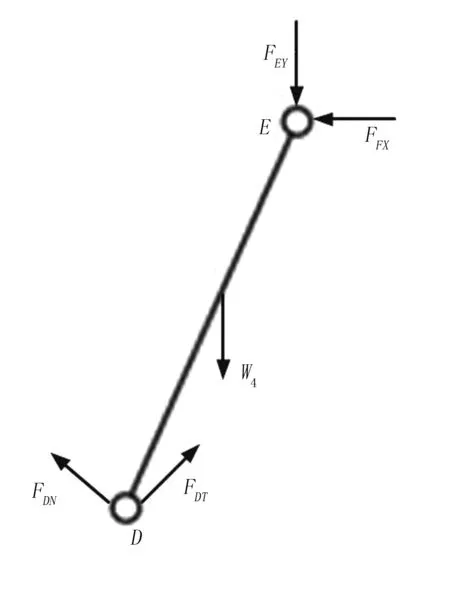
图7 连杆DE受力分析Fig.7 Force analysis of connecting rod DE
根据图7连杆DE的受力情况,建立动力学平衡方程为
FDNcos(α3+φ-π)=0
(10)
FDNsin(α3+φ-π)-W4=0
(11)
(12)
式中m4—连杆DE的质量;
W4—连杆DE所受重力;
x4—连杆DEx轴质心;
y4—连杆DEy轴质心。
2.5EF摇杆受力分析
EF摇杆受力分析如图8所示。
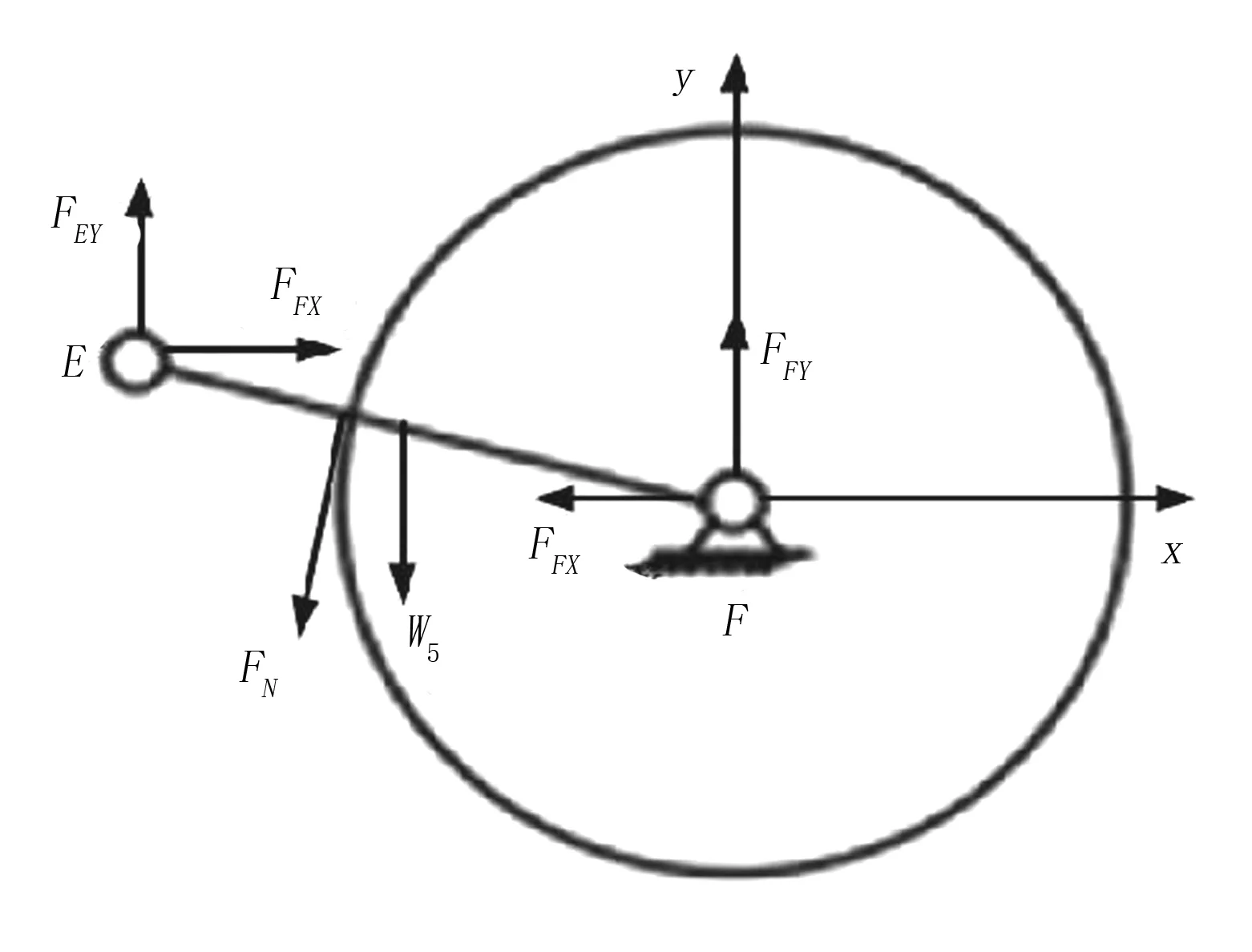
图8 EF摇杆受力分析Fig.8 Force analysis of rocker EF
根据图8摇杆EF的受力情况,建立动力学平衡方程为
(13)
(14)
∑MF=-FEyL5cos(π-α5)-FExL5sin(π-α5)-
(15)
式中m5—摇杆EF的质量;
W5—摇杆EF所受重力;
x5—摇杆EFx轴质心;
y5—摇杆EFy轴质心。
2.6 齿轮受力分析
齿轮受力分析如图9所示。根据图9齿轮受力情况,建立动力学平衡方程为
FfⅡcosβ=0
(16)
FfⅡsinβ-W6=0
(17)
FfⅡsin(π+β)=0
(18)
式中W6—齿轮F所受重力;
R—齿轮半径;
θ—齿轮间压力与x轴间夹角;
β—齿轮间摩擦力与x轴间夹角。
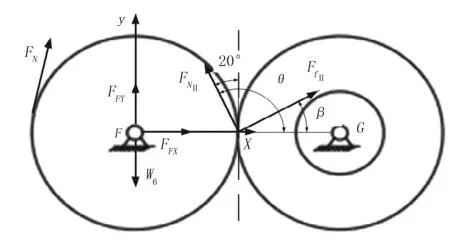
图 9 齿轮受力分析Fig.9 Force analysis of the gear
3 机构动力学仿真分析
通过SolidWorks软件对虚拟样机进行三维数字化建模设计,导入Adams软件里并对机构加入约束。首先对机构进行动力学仿真,本文机械系统采用曲柄定轴转动作为输入,曲柄带动长连杆作用于扇形摆块,扇形摆块通过短连杆作用于摇杆,摇杆通过齿轮轴驱动大齿轮转动1/4圈,齿轮螺母转动1/4圈,丝杠带动苗盘横向运动30mm作为系统输出。此机械系统做间歇运动,摇杆EF顺时针转动90°时,摇杆通过键连接驱动F齿轮转动1/4圈;摇杆EF逆时针转动90°时,齿轮轴带动楔形圆柱凸轮沿着相啮合齿轮的楔形圆柱凸轮面从最低点向最高点滑动。由于两个圆柱凸轮楔形面的相互滑动,切断动力的传递,此时机构间歇。可见,摇杆EF的转动角度对机构准确传动有着很重要的作用。通过软件仿真得出摇杆EF的转角图,如图10所示。
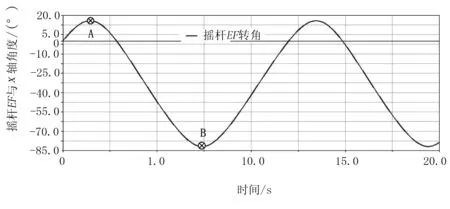
图10 摇杆EF与x轴的夹角Fig.10 The angle between the x-axis and rocker EF
由图10可知:摇杆EF转角曲线上最高点A与最低点B之间的差值大于90°,所以此机构能够实现准确的传动。曲柄摇杆具有急回特性及机构做反复式运动必然产生振动和惯性力,影响机构运动平稳性,限制了机构工作效率。在仿真的过程中,选取了3组曲柄转速,N1=5r/min,N2=10r/min,N3=15r/min。在这3组曲柄转速下,监测了扇形摆块B点的速度和加速度图像如图11所示。

图11 扇形摆块B点速度加速度图像Fig.11 The image of speed -acceleration of the B point on the Fan-shaped swing block
由图 11可以看出:机构的工作转速在N1=5r/min时,扇形摆块B点的速度与加速度变化平稳;当曲柄工作速度N2=10r/min、N3=15r/min时,扇形摆块B点速度与加速度振幅较大,波动显著,机构伴随有强烈的振动,影响机构的正常运行。选取图标中曲柄N3=15r/min时的曲线并结合图 3机构简图来分析曲柄转角与速度加速对应关系,如图11所示。假设在机构简图中水平向右为速度正方向,在图11(a)中a3点和c3点为扇形B点x轴方向速度为零的点,说明曲柄和连杆共线;速度从a3点上升到b3点再下降到c3点,且变化整个过程中速度大于零,说明曲柄转动了1/2圈,即曲柄与连杆的夹角从0°共线变到180°共线。当曲柄与连杆的夹角为90°的时,扇形B点合速度最大,则在水平速度分量也达到最大。同样,在图11(c)中可以分析出图11(a)中相应速度的加速度。根据速度与加速度之间求导关系可知,图11(c)中a3、c3点为图11(a)中a3、c3点的加速度。由此可知:当曲柄与连杆共线时,速度最小,加速度达到最大。图11(c)中,a3为曲柄与连杆夹角为0°时的加速度,c3点为曲柄和连杆夹角为180°时的加速度,且c3点为曲柄和连杆夹角为180°的加速度的惯性力比曲柄与连杆夹角为0°时的惯性力大。图11(c)中b3的加速度为曲柄与连杆夹角为90°时的加速度。通过图11(b)、(d),可以分析出曲柄与连杆之间的对应关系。其中,图11(b)中的a3点为扇形摆块B点在y轴上速度为0,加速度达到最大,曲柄和连杆夹角为0°,意味着B点上升到最高点;图11(b)中的b3点为曲柄和连杆夹角从0°变到180°中的一个角度时所对应扇形块B点的y轴速度分量,此时y轴速度分量最大;从图11(b)中可以看到:速度从c3到g3有一个波动,是因为机构在工作过程中摇杆CB绕定点C转动。在1个工作周期中,扇形摆块B点依次经过Ⅰ-Ⅲ-Ⅱ-Ⅲ-Ⅰ点,且Ⅰ点和Ⅲ点的y坐标点相同,如图3机构简图所示。当曲柄与摇杆之间的夹角为180°时,扇形摆块处于另一个极限位置(即图3中Ⅱ点),y轴速度为0,即图11(b)中e3点、图11(b)中c3点为扇形摆块B点工作弧段中最低点,此时只有x轴速度分量,y轴速度为0。同理,y轴加速度由y轴速度求导可得,对应关系同上。
4 结论
1)对苗盘横向传动机构进行了动力学分析,建立了相应的动力学模型,在对运动学方程求解的基础上,可求各作用力和力矩,并利用计算机进行辅助分析和计算,为得出最优方案提供了理论依据。
2)通过ADAMS软件仿真分析,曲柄的转速对机构的正常运行有着很重要的作用。当曲柄转速分别为N2=10r/min、N3=15r/min时,机构摆块的速度和加速度有明显的波动;当转速调整到N1=5r/min时,机构速度和加速度变化平稳,有利于机构平稳运行。
3)通过仿真图表分析出了扇形摆快速度和加速度和曲柄连杆的位置关系的规律,在曲柄和连杆共线时加速度较大,此时机构惯性力较大,可用曲柄附加平衡块的办法,在到达平衡的同时减少部分惯性力,提高单位时间工作插次,从而提高机构的工作效率。
[1] 王君玲,高玉芝,李成华. 蔬菜移栽生产机械化现状与发展方向[J].农机化研究,2004(2):42-43.
[2] 崔巍,颜华,高希文,等.旱地移栽机械发展现状与趋势[J]. 农业工程,2015(2):15-18.
[3] 左彦军,曹鹏,赵匀,等.B样条非圆齿轮行星轮系水稻钵苗移栽机构的设计与优化[J].农业工程学报,2014,30(15):10-17.
[4] 郭林松,赵匀.平面连杆机构分析解析法的改进及应用设计与研究[J].机械设计与研究, 1995(2):104-110.
[5] 左彦军,曹鹏,赵匀,等.B样条非圆齿轮行星轮系水稻钵苗移栽机构的设计与优化[J].农业工程报,2014(15):10-17.
[6] 李德威,徐凤英.高速曲柄摇杆式分插机构的弹性动力综合设计[J].华南农业大学学报,2001,22(4):81-83.
[7] 郭林松,赵匀.平面连杆机构分析解析法的改进及应用设计与研究[J].机械设计与研究,1995(2):104-110.
[8] 崔巍,方宪法,赵亮,等. 齿轮-五杆取 苗装置机构优化与试验验证[J].农业机械学报,2013(8):74-77.
[9] 赵匀.农机机械分析与综合[M].北京:机械工业出版社,2009.
[10] 李革,应孔月,郑峰君,等. 基于无函数表达节曲线的非圆齿轮分插机构设计与试验[J]. 农业工程学报,2014(23):10-16.
Abstract ID:1003-188X(2017)12-00015-EA
A Study on Dynamic of Transmission Mechanism of Seedling Tray
Li Shufeng, Cao Weibin, Tang Haiyang, Zhao Hongzheng, Liu Jiaodi, Li Hua
(School of Mechanical Electrical Engineering of Shihezi university, Shihezi 832003, China)
Combination of the mechanism among the Crank - rocker ,double - rocker and the gear mechanism, which has a simple structure and reliable operation can achieve precise horizontal transmission of the seedling tray. It is usually used for transporting of the seedling tray. But owing to characteristics of the Quick - return motion and repeated motion ,which have made inevitable vibration and inertial force for the mechanism, It has made a great influence on the effect of smooth motion and working efficiency. Therefore, this article have brought forward a kind of combination of the mechanism among the Crank - rocker double rocker and the gear mechanism for the low upland transplanting seedlings and established the dynamic model of the mechanism. Based on the the dynamic model, the force among the crank, connecting rods, rocker , connection point has been analyzed. A virtual model of transmission machine of the seedling tray was built with ADAMS,which has analyzed the dynamic characteristics in the process of working Using the above method, we can find the cause of vibration, Additional counterweight adding up to the crank is beneficial to reduce some inertial force and to run smoothly, The dynamic analysis on the seedling tray would make a contribute to provide theoretical basis for further optimization design.
transplanting mechanism ;transmission of the seedling tray ;dynamics ; ADAMS
2016-10-09
国家自然科学基金项目(51565048)
李树峰(1972-) ,男,沈阳人,硕士研究生,(E-mail)lilshufeng1029@qq.com。
曹卫彬(1959-),男,湖北襄阳人,教授,博士生导师,(E-mail)wbc828@163.com。
S223.92;S220.3
A
1003-188X(2017)12-0015-05
