背景分析透灵感自然来

☉重庆大渡口区教师进修学校 廖帝学

背景分析透灵感自然来

☉重庆大渡口区教师进修学校 廖帝学

一、原题呈现

下面这道题来自2016年4月重庆市巴南区中考适应性考试试题.

如图1，在矩形ABCD中，点E、F分别在边BC、CD上，且∠EAF=∠CEF=45°.若AD=9，DC=8，则EF的长为____________.

图1

二、问题“背景”分析及解法展示

1.对题目的初步研判.

原题所给条件简洁，数据简单，图形清新，其中的“半角模型”给人以似曾相识之感.高中数学有“两角和的正切公式”，我们知道：若α、β均为锐角则α+β=45°.此题我们不妨可以看作这一背景知识在初中的应用.稍加思考，我们会发现当BE=4、DF= 3时即可满足要求，此时CE=CF=5，EF的长为

但是，这是教师以“高观点”分析问题“背景”从而快速地得出了题目的答案.从这里我们也可以看出，解题思路的形成、解题方法的获得与解题者的知识储备、解题经验的积累关系很大.一般的初中生是断然不会用这种方法解决此题的.

命题者怎样命制此题的呢？命题者期望的解法是什么呢？下面让我们一起来看一道中考试题.

（2015·福建三明市中考题）在正方形ABCD中，点E、F分别在边BC、CD上，且∠EAF=∠CEF=45°.

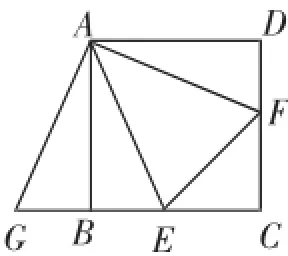
图2

图3

（1）将△ADF绕着点A顺时针旋转90°，得到△ABG（如图2），求证：△AEG≌△AEF；

（2）若直线EF与AB、AD的延长线分别交于点M、N（如图3），求证：EF2=ME2+NF2；

（3）将正方形改为长与宽不相等的矩形，若其余条件不变（如图4），请你直接写出线段EF、BE、DF之间的数量关系.

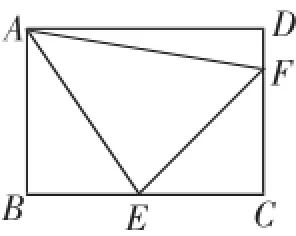
图4

图5

相信我们能够看出来，将这道中考题的第（3）问提取出来就是我们前面呈现的“原题”.由于有第（1）（2）两问的铺垫，将图4按图3的方式补成图5，易得EF2=2BE2+ 2DF2.当AD=9，DC=8时，设CE=CF=x，则BE=9-x，DF=8-x，则2x2=2（8-x）2+2（9-x）2，解得x1=5，x2=29（舍去），故EF的长为

事实上，我们还知道，EF2=ME2+NF2这个结论的得来，既可以通过旋转，也可以通过翻折得到，如图6、图7所示.

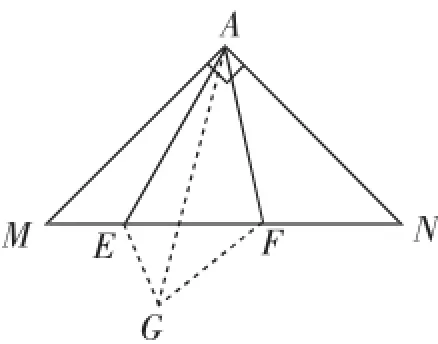
图6

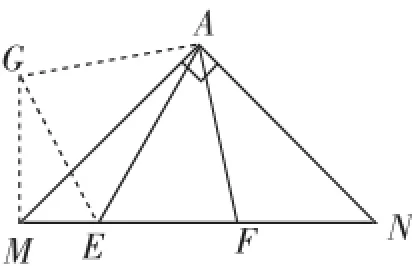
图7

的确，如果解题者能够迅速发现原题的这些“背景”，解答此题应该较轻松.但是，毕竟原题并没有为我们作太多铺垫.面对此题，不是每一个人都会这样思考，就算按这样的思路思考也不一定能发现此题的本源.从“在矩形ABCD中，点E、F分别在边BC、CD上，且∠EAF=∠CEF=45°”这些简单“背景”出发，解题者会从哪些方向思考呢？下面来看原题的其他解法.

2.原题的其他解法展示.

原题中，结合大家都熟识的“半角模型”，若AB=AD，“旋转”就有可能.但题目中AB和AD偏偏不相等.是否可以旋转呢？

解法1：如图8，将△AFD绕点A旋转90°后，点F的对应点为点G.连接GE.易得△AGE≌△AFE.设CE=CF=x，在Rt△EGH中，由勾股定理，可得（，解得符合条件的x的值为5.

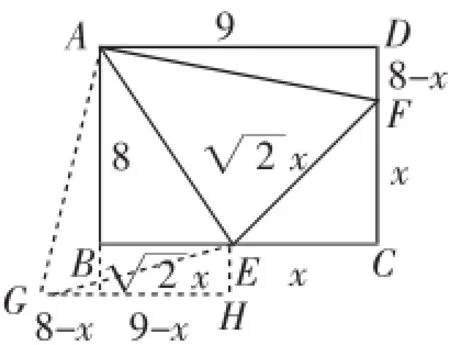
图8

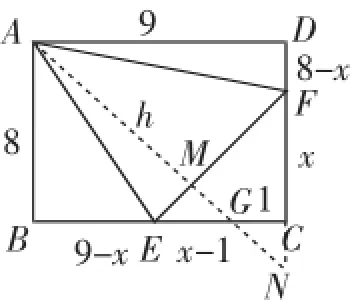
图9

当然，条件中的“∠EAF=∠CEF=45°”给人很大的想象空间，围绕着它我们还可以得到下面几种解法.

解法2：如图9，作∠BAD的平分线分别交EF、BC、DC的延长线于M、G、N.易得△AEM∽△AFD，△ABE∽△AMF.设CE=CF=x，则，整理得x2-34x+145=0，解得x1=5，x2=29（舍去），故

解法3：如图10，作BE=BG，DH=DF，易证△EGA∽△AHF.所以，解得符合条件的x的值为5.

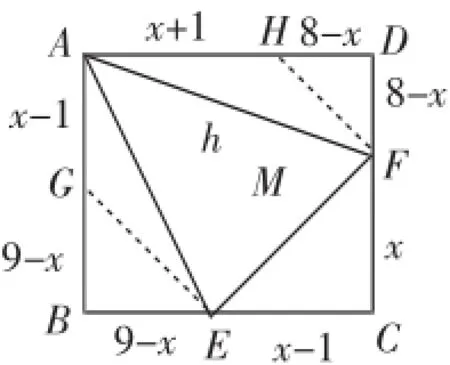
图10

解法4：如图11，过点E作EH⊥AF于H.易知∠1=∠2，所以△ABE∽△EHF.设CE=x，EH=y，由又因为在Rt△ABE中，由勾股定理，得，同样可得符合条件的x的值为5.

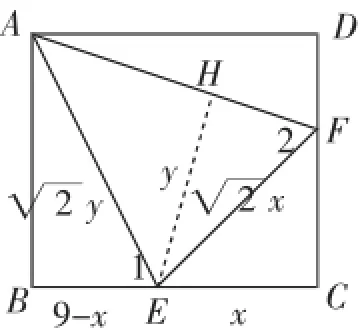
图11

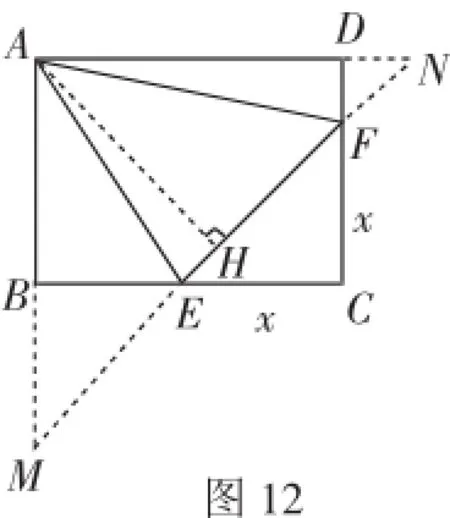
图12

解法5：如图12，EF所在直线与AB、AD的延长线分别交于M、N.过A作AH⊥EF于H.易证△AHE∽△ADF，△ABE∽△AHF，则所以则AH.设CE=x，则AM=AN= 17-x.由

三、“背景”分析透，“灵感”自然来

一道看似不甚起眼的“小题”有多种不同的解法，类似的现象在数学学习过程中并不鲜见.“你为什么要这么解呢？”“你是怎么想到这种解法的呢？”面对每一种解法，我们总喜欢这样去询问解答者.而解答者的回答中，最爱说的就是：灵感.

什么是灵感？在数学教育家中对它的论述较多的当推波利亚.散见于他的著作中的许多片断表明，他相信并重视灵感.他的《怎样解题》一书的中心思想就是谈解题过程中如何诱发灵感.他说，在解题活动中我们要设法“预测到解，或解的某些特征，或某一条通向它的路.如果这种预见突然闪现在我们的面前，我们就把它称为有启发性的想法或灵感.”

对于“灵感”，我们爱用“蹦出”“闪出”“闯进”“一闪念”等来描述它，的确，“灵感”有它的自发性和随机性.但是，事实上，“灵感”的得来绝对不是无缘无故.

波利亚在“怎样解题表”中曾这样提出：

你知道一个与此相关的问题吗？

试想出一个具有相同或相似未知数的熟悉的问题.

你见过相同的题目或形式稍有不同的问题吗？

……

前述题目的每一种解法的得来或许都有灵感，但更多的仍是对题目条件、背景的深入分析之后的结果.从“45°”“矩形”等条件出发，从图形的简洁、美观出发，有的人联想到了平时的“半角模型”，有的人想方设法构造等腰直角三角形，有的人努力寻找相似三角形……这其实就是在“诱发灵感”.这个过程就是不断变更问题的探索过程.事实上，只要将题目的“条件”“背景”不断变更、不断探索，一旦分析透彻、到位了，“灵感”自然也就来了.可见，“背景”是灵感的诱因，而要获得灵感，唯有正向的“探索”才是真正的捷径.

1.李静静.利用网格构造图形求解三角函数值［J］.中小学数学（中），2016（5）.

2.胡书军等.解题思路的生成才是解题教学的重中之重［J］.中学数学教学参考（上），2016（5）.

3.詹高晟，苏德杰.一道中考试题的命制与感悟［J］.中学数学（下），2015（11）.