去括号的本质与教学思考

☉江苏第二师范学院章飞

去括号的本质与教学思考

☉江苏第二师范学院章飞

在国培等活动中与一线教师交流时，大家对去括号及其依据有些争议，为此，笔者有了下面的思考，与大家共研.

一、括号的作用（为什么先算括号里的？）

括号，本就是用来规定运算次序的符号.我们看几个算式：3×5-4+6，3×（5-4）+6，3×（5-4+6）.没有括号时，运算顺序是自然的“×、-、+”.为了保证先进行某些运算，数学上引进了括号，将括号内看成一个整体，自然括号内优先运算了，如后面两者的运算顺序变成了“-、×、+”和“-、+、×”.

实际上，算式左边有n个数，最终结果是1个数，中间过程中需要进行n-1次运算，这n-1次运算本身应该有先后的，为了体现这样的运算顺序，需要依次通过“（）”加以体现，这样，就应该有n-2个“（）”.例如，上面的“3×5-4+6”，严格地讲，应该是“［（3×5）-4］+ 6”.显然，这样表示容易使人“眼花缭乱”，为了求简，应尽可能减少“（）”，因此，就得有其他补充规定：没有括号的先算乘除，再算加减；同一级的运算，按照从左往右的顺序进行.

二、去括号的本质（为什么要去括号？）

根据上面所说“括号的作用”，不难知道，增补括号的目的是改变运算的顺序，因此，去除括号的目的还是改变运算的顺序.增补或者去除括号都不能减少运算个数，只是改变顺序.

那么又为什么要通过去括号来改变顺序呢？实际上，这是为了将式子转化成各项的代数和形式，然后进行同类项的合并.

我们先看一个例子：

图1

按图1的方式搭n个这样的正方形需要几根火柴？你是怎样得出来的？

学生从不同的角度得出不同的算式：4+3×（x-1），1+ 3×x，2×x+（x+1），4×x-（x-1），显然这几者应是相同的，如何说明它们相同呢？看来需要化简为较简单的形式1+3× x，这就需要首先将括号去掉，转化为只有x和常数的项，然后合并.也就是说，去掉括号后，可以更好地看出所谓的同类项，然后才能合并同类项.

去掉括号后，就自然可以合并了吗？全部转化为一些项的和或差的形式，这时，从初中数学中代数和的角度加以理解，都是若干项的和，因此，根据加法运算的交换律和结合律，这些加数可以随意组合，这样就可能简便运算了.我们看下面的例子：

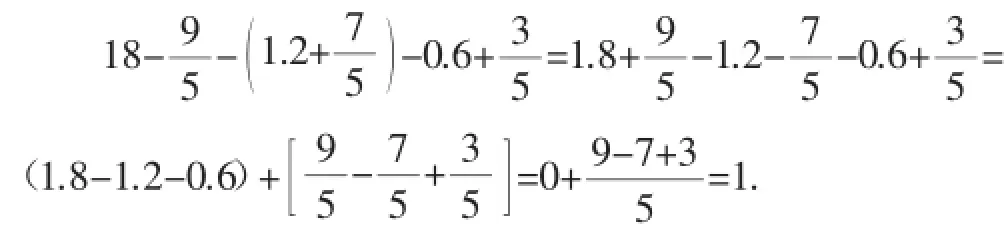
三、去括号的法则（怎么去括号？）

怎么去括号？自然遵循去括号的法则：

括号前是“+”的，把括号和它前面的“+”去掉后，原括号里各项的符号都不改变；

括号前是“-”的，把括号和它前面的“-”去掉后，原括号里各项的符号都要改变.

那么，“2（x-1）=2x-2”属于去括号吗？从形式上看，也去掉了括号，但感觉和去括号的法则不一致，另外这里左边是3个数，两个运算，右边只有两个数，1个运算，也就是这个过程中已经完成了一个运算，即已经完成了2与（x-1）的乘法，所以，这个不是我们一般意义上的去括号，而是乘法运算.

我们不妨再看一个复杂的.

7p2-1-2（p2-p），因为有括号，运算顺序是：p2-p、2（p2-p）、7p2-1、7p2-1-2（p2-p），四次运算.如果直接化成“7p2-1-2p2+2p”的形式，运算顺序是：7p2-1、7p2-1-2p2，7p2-1-2p2+2p，可见，这样不仅改变了运算顺序，而且少了一步.也就是说，这里实际上完成了两个任务，去括号（改变运算顺序）的同时完成了“×2”这一动作，因此，这不是一般意义上的去括号.这也是一些潜能生容易发生错误的原因.按照去括号的步骤，应该是：

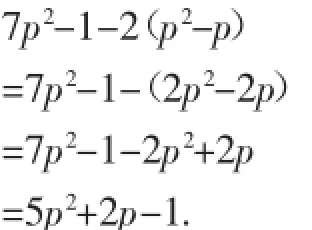
其中，第一个等号是进行乘法运算，依据是分配律，第二个等号才是去括号.

四、去括号的依据（为什么可以这样去括号？）

根据上面的分析，下面等号左边变为右边的过程叫去括号.

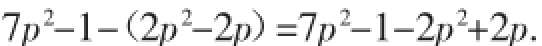
对于小学生而言，其依据是加减法的运算规律（单调性）：

两数相减，如果被减数不变，减数加（或减）一个数，差反而减（或加）这个数.

将减数（2p2-2p）看成2p2，多减了2p，结果少了2p，得加上来.

对于初中生而言，其依据之一是相反数的意义：减去一个数，等于加上这个数的相反数.

7p2-1-（2p2-2p）=7p2-1+（-2p2+2p），实际上，这里还有括号（即先算-2p2+2p）.根据加法运算的结合律与交换律，可以改变各项的运算顺序为7p2-1-2p2+2p（相当于［（7p2-1）-2p2］+2p）.即在由7p2-1+（-2p2+2p）变为7p2-1-2p2+2p的去括号过程中，依据是加法的交换律和结合律.

所以，去括号的依据是加减法的意义和加法的交换律和结合律.

五、去括号法则的教学（去括号怎么教？）

去括号法则的教学中，应注意引领学生依次完成下面几项工作：通过情境感受去括号的必要性，自主探究并归纳总结去括号的法则，在运用中巩固去括号的法则.部分学生具有将括号前面的系数融合到去括号过程中的能力基础，因此，可以在运用巩固去括号法则的过程中通过师生的交流引出这样的“简便”做法，从而使得部分学生可以灵活运用法则.具体地，可以有类似下面的教学设计.

（一）情境引入.

还记得前面学习的一个案例（参见图1）吗？相信大家在探索过程中一定得到了多种结果：4+3×（x-1），1+3× x，2×x+（x+1），4×x-（x-1）.同一个问题，竟然有多种不同的表示方式，我们自然需要思考：这些式子既然表示同一个事物，它们肯定是相等的，那么怎么相互转化呢？这些式子中哪个式子较为简捷？其他式子与这个式子的差别在哪里？怎么消去这个差别？从而引出需要去括号（点明课题）.

（二）探究法则.

1.根据上面的情境，2x+（x+1）=3x+1，4x-（x-1）=3x+ 1，你能从代数运算的角度说明其中的道理吗？

2.反思交流.

相信大家不难发现：2x+（x+1）=2x+x+1=3x+1；4x-（x-1）=4x-x+1=3x+1.每个式子中第一个等号将括号去掉了，这就是去括号.请借助上面的经验去掉下面各式中的括号，并借助具体数据验证你的结论（提供4个括号前面仅有正负号的式子，略）.

3.归纳法则.

根据上面的经验，不难归纳出去括号的法则：

括号前是“+”的，把括号和它前面的“+”去掉后，原括号里各项的符号都不改变；

括号前是“-”的，把括号和它前面的“-”去掉后，原括号里各项的符号都要改变.

（三）运用法则（去括号，括号前面仅有“+”“-”，略）.

（四）变式发展.

1.情境再现.

（1）如何说明4+3（x-1）=3x+1呢？

（2）一般地，括号前面还有不是1的系数，怎么将括号前面的系数去掉呢？

引导学生先将括号前面的系数乘进括号里再去括号.

2.运用巩固（提供几个括号前面有系数的式子，进行去括号的强化训练，略）.

3.反思交流.

在巡视中发现有学生是这样去括号的：4+3（x-1）= 4+3x-3=3x+1，你能说说这样做的道理吗？在讨论的基础上明晰：这样做，实际上是将其中一步4+（3x-3）省去了，简洁了一些，但跳步可能增加出错的风险哟.将来，如果确信自己不会出错的情况下，可以省去这一步，如果没有把握，当然还是老实点儿不要跳步了.

这样设计，既保证了算理清晰，没有争议，又给了学生选择的空间，可以按照自己的学力水平灵活选择适切的方式.多数学生能够按照算理步步为营，正确地得到结果，潜能生也能跟得上，又允许了学优生直接跳步.

1.章飞，凌晓牧.初中数学研究与教学指引［M］.北京：北京师范大学出版社，2012.