“探究四点共圆”课例的课堂实施

☉江苏苏州市高新区实验初级中学葛存燕

“探究四点共圆”课例的课堂实施

☉江苏苏州市高新区实验初级中学葛存燕

近年来，《中学数学》（下）刊发了大量预设精妙的教学课例，引领一线教师聚焦课堂教学设计，追求高质量的备课设计.笔者受到文1的影响，通过自己的理解，制作出对应的PPT，执教了一节研讨课，取得了较好的教学效果.本文梳理该课的教学流程，侧重于截图展示笔者的PPT流程，并跟进变式检测，供研讨.

一、教学流程

教学环节（一）作三角形的外接圆，引入新课.

PPT截图，如图1：

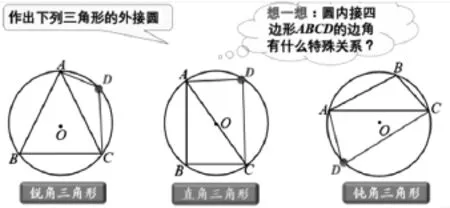
图1

解读：先呈现三种不同形状的三角形（锐角三角形、直角三角形、钝角三角形），再画出外接圆，并增加一个点D，出现圆的内接四边形.

在此基础上，引导学生思考问题.

教学环节（二）探究并证“四点共圆”.

PPT截图，如图2：

图2

PPT截图，如图3：

图3

解读：由于在初中阶段对反证法的要求是了解，故这里只是以PPT呈现证明思路，不要求所有学生独立证明.

教学环节（三）发现“四点共圆”.

PPT截图，如图4：

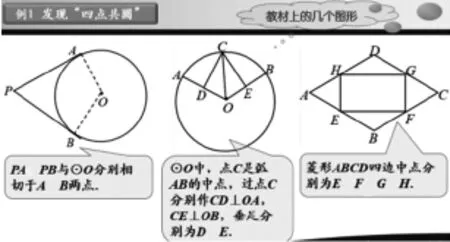
图4

解读：所选的几个图形都是教材上的一些经典图形，安排学生从四点共圆的角度再次研究、关注，也是一种“高观点”视角.

PPT截图，如图5：

图5

解读：例2所配发的3个图形中四边形并不需要都画出外接圆，引导学生体会圆在脑中，享受思考的乐趣.

PPT截图，如图6：

图6

解读：这是八年级一道经典试题，引导学生站在九年级四点共圆的高度重新反思和理解这道题的不同解法，体会数学解题的殊途同归.教材上关于正方形的经典问题很多，比如还有另一道，见PPT截图，如图7：

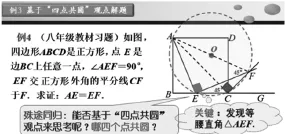
图7

解读：对于该题，在八年级时需构造全等证明，而站在四点共圆的角度，可以获得问题的结构认识.

教学环节（四）课堂小结，听课检测.

启发学生思考：如何证明多点共圆的方法，以下是一些可能的思考念头，比如：

1.从圆的定义出发，证各点都与某一定点的距离相等；

2.如果是证四点共圆，也可以先任意选出三点作一圆，然后证另一点也在该圆上；

3.如果各点都在某两点所在直线的同侧，且各点对这两点的“张角”（其实是同弧所对的圆周角相等逆向使用）相等，那么这些点共圆；

4.若能证明其对角互补或证明其一外角等于其邻补角的内对角，即可肯定这四点共圆；

5.证明五个或五个以上的点共圆，可以分别证各四点共圆，且四点中有三点相同.

附1：听课检测题：

1.如图8，在四边形ABCD中，∠ABC＝∠ADC＝90°.

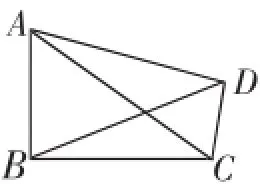
图8

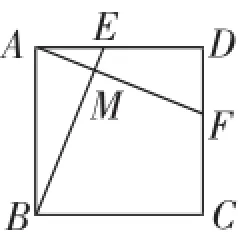
图9

（1）A、B、C、D四个点_______在同一个圆上；（填“能”或“不能”）

（2）当∠ABD＝70°时，∠CAD的度数是_______.

2.如图9，点E、F分别在正方形ABCD的边AD、CD上，且AE＝DF，连接BE、AF交于M点.

（1）小南经过思考发现点E、M、F、D在同一个圆上！请判断小南的发现是否正确.如果正确，在图中作出该圆的直径；如果不正确，说明理由.

（2）连接CM、BF，若∠FBC＝35°，求∠FMC的度数.

※挑战：（3）延长AF、BC交于点N，若点B、M、D、N在同一个圆上，求证：E为AD的中点.

二、教学思考

1.研习专业期刊，积极实践跟进.

我们知道，研习专业期刊是青年教师追求专业精进的重要途径，然而如果只是阅读、欣赏而缺少必要的实践跟进，往往入宝山而空返.基于此，我们提倡面对优秀课例的教研文章，作为读者的我们要细心捕捉文章中课例设计的精巧与经营之功，并积极在自己的教学实践中开展教学，这样往往会对优秀课例的理解更加深刻和独到.比如，在上文中我们跟进实践之后就知道了哪些教学环节还需要深入构思、预设互动，哪些环节学生在见到问题之后就可以一带而过，无需充分展开.

2.丰富教学设计，预设对话追问.

在决定使用本文课例进行教学实践之前，我们针对教学设计制作了PPT，上文侧重展示了各张PPT及解读.我们发现制作PPT的过程，仍然是加深对四点共圆理解的过程，如何让四点共圆问题提出得更加自然，思考得更加合理，让证明的念头更容易获得；所选配的例题、习题怎样引导学生基于四点共圆的视角进行求证，当学生思维受阻时，如何预设一些标注语启发学生自主获得思路贯通，等等，都是值得我们深入构思之处.

3.加强教学反馈，注重听课检测.

我们在课堂最后增设了听课检测，通过改编课堂中的例题及拓展讲评的例题，设计出2个大题5个小问的模式，这样既便于检测学生，又可以启发思考，感受经典问题解法的多样性、思路解法的殊途同归.

本文中一些草根实践，才刚起步，抛砖引玉，期待更多同行的实践跟进.

1.%王友峰.专业自主增设内容，回看陈题洞察结构——九年级“探究四点共圆”教学设计与解读［J］.中学数学（下），2016（12）.

2.周红娟.开放与放开：概念生成与例题变式的教学追求——从“三角形内角和”教学说起［J］.中学数学（下），2016（8）.

3.郑毓信.善于举例［J］.人民教育，2008（18）.

4.郑毓信.善于提问［J］.人民教育，2008（19）.

5.郑毓信.善于优化［J］.人民教育，2008（20）.