重构教材，让学生的思维自然生长——“线段、射线、直线（第1课时）”的教学创新设计与思考

☉江苏南京市中华中学上新河初级中学黄玉华

重构教材，让学生的思维自然生长
——“线段、射线、直线（第1课时）”的教学创新设计与思考

☉江苏南京市中华中学上新河初级中学黄玉华

2013年11月在江苏省第四届“心桥杯”六校教改联盟（黄桥）——“推开问题的大门”课堂教学研讨活动中，笔者执教的苏科版数学七年级上册第六章第一节“线段、射线、直线（第1课时）”，以培养学生“四能”为立意，赢得了与会教师的高度评价，并撰写文章《培养问题意识，推开问题大门》发表于《中学数学》（下）2014年第3期.2016年11月，在南京市初小数学衔接教学研讨活动中，笔者又重温此课，重新设计，以发展学生思维为立意，收到了与会老师的好评，在此撰文与各位同行分享交流.

一、教学实录

1.操作探究，唤醒学生思维.

师：小学里我们已经认识了线段、射线和直线，请同学们各画出一条线段、射线和直线，说说它们的区别.

生：线段有两个端点，射线只有一个端点，直线没有端点.

生：线段不能延伸，射线只能向一个方向延伸，直线可以向两个方向延伸，线段有长度，射线和直线没有长度.

师：请你过一点画直线，你能画几条？过两点画直线，你能画几条？

生：过一点可以画无数条直线，过两点只能画一条直线.

师：通过实践发现，过两点能画一条直线并且只能画一条直线，这个基本事实，我们可以概括为“两点确定一条直线”，这里的“确定”如何理解？

生：“有且只有”的意思.

师：对，这里的“确定”一词有两层含义，一是经过两点有一条直线，表示存在；另一层含义是经过两点的直线只有一条，表示唯一.这就是数学语言的简洁美！今后我们可以把这个结论作为说理的依据.下面，我们来看一个应用，每年的3月12日是植树节，你用什么方法可以使植的树在一条直线上？

生：只要定出两个树坑的位置就能确定同一行树所在的直线.

设计意图：这里主要安排了两个活动.活动1让学生画线段、射线和直线，从形上直观感知它们的区别，起到唤醒学生的思维的作用.活动2则通过操作体验得到了基本事实“两点确定一条直线”，这是“用两个点表示一条直线”的理论基础，为下面的“线段、射线、直线”的符号表示奠基.另外应用这个基本事实解决了如何使“植的树在一条直线上”的实际问题，能使学生感悟到数学来源于实际又服务于实际，培养学生理论联系实际的思想.

2.问题探究，引领学生思维.

师：如何区别黑板上两条不同的线段、射线、直线呢？下面我们就一起来探究它们的表示.请同学们结合下面的几个问题进行思考.

问题：（1）怎样用符号表示线段、射线和直线？表示的字母有什么注意点？有几种表示方法？

（2）怎样由一条线段得到射线和直线？你能用准确的语言描述吗？

（5分钟后）

师：请同学们将学习过程中的问题提出来，小组内进行交流.

（3分钟后）

师：刚才同学们学得很认真，交流也很激烈，下面来看看大家掌握得怎么样.线段怎样表示？

生：线段可以用表示端点的两个大写字母表示，也可以用一个小写字母表示，如甲同学画的线段可以记作线段AB、线段BA或线段a.

师：对，所以表示线段的两个字母没有顺序！乙同学画的这条线段如何表示？

生：两个端点字母可以用大写字母C、D表示，记为线段CD或线段DC，也可以用一个小写字母b表示，记为线段b.

师：请同学们看屏幕，你能用语言描述怎样由一条线段得到一条射线吗？（屏幕上展示的是将线段AB由A向B方向延长时得到一条射线的动画）

生：延长线段AB.

师：描述很准确，这里延长线段AB是指按从点A到点B的方向延长.这条射线如何表示呢？

生：射线A.

师：这样表示准确吗？（见学生未有反应，教师以点A为端点画另一条射线，如图1所示）

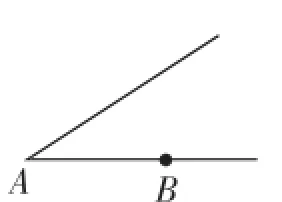
图1

生：不准确，还要再在射线上找一点，表示射线的延伸方向，即表示成射线AB.

师：这里的A表示端点，B表示射线延伸方向上的任一点，表示射线的端点的字母必须写在另一个字母的前面.

师：请同学们看屏幕，你能用语言描述这条射线怎样得来的吗？（屏幕上展示的是将线段AB由B向A方向延长时得到一条射线的动画）

生：延长线段BA.

师：还可以怎样描述？

生：反向延长线段AB.

师：对，反向延长线段AB是指按从点A到点B的方向的反方向即从点B到点A的方向延长.这条射线，如何表示？

生（齐）：射线BA.

师：那么乙同学画的这条射线如何表示？

生：端点字母设为M，在这条射线上另取一点记为N，表示为射线MN.

师：很好！如果再在这条射线取一个点E，怎样表示？再取一点F呢？

生（齐）：射线ME、射线MF.

师：表示同一条射线有多少种不同的表示方法呢？

生：有无数种，用射线的端点和它延伸方向上任一个点就可以表示.

师：能用一个小写字母来表示一条射线吗？

生：不能，因为射线的特征是有一个端点和一延伸方向，如果用一个小写字母表示就不知道端点和延伸方向了.

师：对，分析得很到位，因此，表示射线时不能像表示线段那样用一个小写字母来表示.请同学们看屏幕，你能用语言描述这条直线怎样得来的吗？（屏幕上展示的是将射线AB反向延长时得到一条直线的动画）

生：延长线段BA.

生：反向延长射线AB.

师：同学们的描述都非常正确，那直线怎样表示？

生：在直线上任取两个点A、B，记为直线AB或直线BA，也可以用一个小写字母m表示，记为直线m.

师：为什么在直线上任取两个点就可以表示一条直线呢？

生：两点确定一条直线！

师：对，有理有据，所以表示直线与表示线段类似，表示直线的两个字母也没有顺序！

设计意图：设计问题串引导学生进行自主探究，不仅可以提高学生自主学习的效果，而且可以让学生在思考问题的过程中，不断地发展思维、完善思维、引领思维，把学生的思维不断推向深入——线段、射线、直线之间有什么联系与区别？如何用运动的观点理解这种联系与区别？如何表示？突出了数学的本质，为下面应用它们解决有关问题奠定了基础.

3.练习巩固，优化学生思维.

（学生口答，教师追问）

（1）如图2：

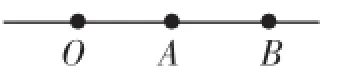
图2

①射线OA与射线OB是同一条射线吗？

②射线OB与射线AB是同一条射线吗？

③射线OA与射线AO是同一条射线吗？%

（2）请你判断下列表示方法是否正确：

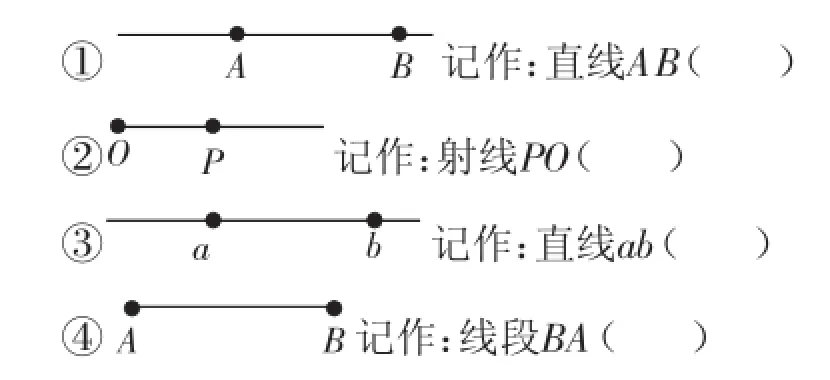
（3）如图3，在直线m上有3个点A、B、C，图中以A为端点的线段有哪几条？

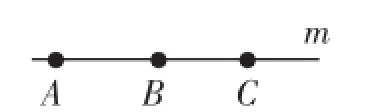
图3

师：你能提出什么问题考考其他同学们吗？

生：图中以B为端点的线段有哪几条？

生：有线段BA、线段BC.

生：图中共有多少条线段？

生：共有3条，线段AB、线段AC、线段BC.

生：图中以A为端点的射线有哪几条？

师：这个问题提得很好，我们不仅学习了线段，还有射线和直线！谁来解决一下？

生：两条，从点A向右的射线可记为射线AB或射线AC，但向左的……（犹豫不决）

师：从点A向左的是一条射线，但要表示它还需要再在点A左侧的射线上另取一点，才可表示，直线上的一个点将直线分成几条射线呢？

生：两条.

师：还能提出什么问题吗？

生：图中以B为端点的射线有哪几条？

生：图中以C为端点的射线有哪几条？

生：图中共有多少条射线？

生：图中共有多少条直线？

……

（教室里沸腾起来了）

师：同学们提出的问题真不少！如果在直线l上有n（n≥2）个点，那么图中共有多少条线段？多少条射线？请同学们课后去研究.

设计意图：对数学概念的认识，必须从正、反两个方面进行强化，这里设计了一组问答题和判断题，有效地从正、反两个方面帮助学生强化对线段、射线、直线概念的理解，特别是对同一条射线必须满足两同（端点相同，从端点射出去的方向相同）的认识；在这个基础上，利用图3，在教师先示范性地提出一个问题的基础上，让学生尝试着提出不同的问题，着力培养学生的问题意识；由学生自己提出问题，思维具有一定的开放性，教师在此基础上，进行归纳，提出一个一般性的问题，并将问题的探索延伸至课外.

4.回归生活，活化学生思维.

活动1：

师：如图4，从甲地到乙地有3条路，走哪条路较近？

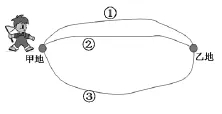
图4

生（齐）：路线2.

师：从甲地到乙地能否修一条最短的路？如果能，你认为这条路应该怎样修？请在图中画出这条路.

生：从甲地到乙地修一条线段.

师：结合生活经验，同学们能概括出一个结论吗？

生（齐）：两点之间线段最短.%

师：今后我们可以将这个结论作为说理的依据，下面我们来看一个应用.2005年之前，我们台湾同胞要从高雄机场赶到北京机场需要绕道香港机场，全程约为2654km，同学们觉得应该怎样设计航线使得行程最短呢？为什么？

生：从台湾直达北京，两点之间线段最短.

师：对！经多方努力协商，2005年开通了台湾与北京的直航，全程约为2098km，不仅缩短了海峡两岸的距离，更拉近了同胞们的心灵的距离.你认为用哪一个数据来刻画北京与高雄两地的距离更为合理？

生：2098km.

师：对，我们把连接两点所得线段的长度，叫作这两点之间的距离，所以北京与高雄两地的距离就约为2098km，要注意两点之间的距离是连接两点的线段的长度，是一个数量，它与线段是不同的.

设计意图：这里设计了一个活动，让学生根据生活经验来感受基本事实“两点之间线段最短”，然后应用这个基本事实来解决实际问题，进而得出了两点之间距离的概念，使得结论的发现、概念的由来、思维的发展水到渠成、一气呵成.

5.综合拓展，深化学生思维.

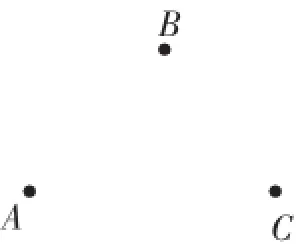
图5

出示三道练习题：

（1）做一做：如图5，已知点A、B、C.

①画线段BC（连接BC）；

②画直线AB、AC；

③在线段BC上取一点D，画射线AD.

（2）如图6，看图说话（用几何符号语言描述图6中两个图形）

图6

（3）赛一赛：看图、说图、画图.

图7

比赛规则：

同桌两名同学，一人面向屏幕，另一个人反向.其中一名同学看着屏幕上提供的图7所示的图形说给另一名同学听，另一名同学在纸上画出大致的图形，比哪一组完成得既对又快.然后两人互换角色.

（赛一赛，教室里再次沸腾）

设计意图：这里，第（1）题是读句画图，训练学生由符号语言转化为图形语言的能力；第（2）题是看图说话，训练学生由图形语言转化为符号语言的能力；第（3）题是综合运用题，考查学生三种语言相互转化的能力.

6.小结交流，升华学生思维.

学生自主小结线段、射线、直线的区别、符号表示、两个结论，学习过程中获得的经验和方法，在回顾和感悟中提升知识的运用能力.

师：本节课的内容可提炼成“3332”，即学习了3种图形、3种概念、3个语言和2条结论，同学们还有什么问题吗？

生：过一个点可以画无数条直线，过两个点可以画一条直线，那么过3个点、4个点、…，可以画多少条直线呢？

师：你提的问题真好！请大家课后思考一下.本节课同学们不仅能解决老师提出的问题，而且能积极主动观察、思考、发现问题，还提出很多有价值的问题，推开了问题的大门.希望同学们认真学好数学知识，领会数学思想，培养问题意识，勇于创新，争取取得优异的成绩！下课.

设计意图：以问题单的形式引导学生进行总结反思，在学生自主小结的基础上，抓住线段、射线、直线的异同，教师及时进行提炼，帮助学生形成两类结构即知识结构和方法结构；利用学生谈收获和体会的契机，帮助学生积累基本活动经验；要求学生提出新的问题，有利于进一步培养学生的问题意识，也为下一节课的教学打下了基础.

二、教学思考

《标准》指出：“教材内容的选择应符合课程标准要求，体现学生的身心发展特点，有利于引导学生利用已有的知识与经验，主动探索知识的发生与发展，同时也有利于教师创造性进行教学.”数学教材为师生开展数学学习活动提供了主题、线索和结构，是实现数学课程目标、实施数学教学的重要资源.应该说教材的编写，凝聚着很多专家和教师的心血与智慧，但教师不仅是教材的使用者，同时也是教材的开发者.叶圣陶先生也说过：“课本只是一个例子”.教师只有准确把握《标准》，深刻理解教材，深入钻研学情，才有可能根据课本这个例子，创造性地使用教材，为“思维而教”.

1.了解学情，让思维的衔接平滑、自然.

研究学生，了解学生，掌握思维的起点，是让学生思维自然生长的前提之一，是为“思维而教”的基础.因此，教师应当对学生已有的知识、方法、经验作出更为深入和具体的分析，为教师的备课及课堂教学的实施打下坚实的基础.关于“线段、射线、直线”，学生在小学里已经具备的知识和生活经验主要有：（1）通过具体情境认识了线段、射线、直线的相关概念；（2）知道直线是向两个方向无限延伸的，射线是直线上一点和它一旁的部分，线段是直线上两点和它之间的部分，直线上一点把直线分成两条射线，直线上两点把直线分成一条线段和两条射线，射线上一点把射线分成一条线段和一条射线；（3）线段、射线、直线的主要区别是端点个数不同，线段有两个端点，射线有一个端点，直线没有端点；（4）掌握度量线段的长度、画指定长度的线段的技能.由于执教的是一所城乡结合的初中的学生，学生不善于发表独立见解，发现和提出问题的能力、分析和解决问题的能力都比较弱，但他们具有很强的好奇心，对小学里关于“线段、射线、直线”的知识掌握较好，对线段、射线、直线这些图形的生活原型很熟悉，所以教者在教学中以画出线段、射线、直线模型为抓手，抓住前后知识的联系，充分利用学生的知识最近发展区，引导学生拾级而上，不断地发现和提出问题，并帮助他们学会有条理地分析和解决问题，积累初步的数学活动经验，达到思维无缝衔接的效果.

2.重构教材，让思维的产生符合逻辑.

课堂教学离不开教材，任何一个版本的教材，都是专家精心编写而成的，但教材仅是一例子，我们应该在理解课标、理解教材、理解学情的基础上，科学、合理地使用教材，用教材教，而不是教教材.本节课教材编写的顺序是：通过问题情境和观察、操作，探究得到基本事实“两点之间线段最短”，同时介绍两点之间的距离这一概念；接着探究用符号表示线段、射线、直线，并以“议一议”的活动强化对线段的认识；然后通过问题情境和观察、操作，探究得到基本事实“两点确定一条直线”；最后设计了读句画图的活动，巩固三种语言的互译.本节课的重点是线段、射线和直线的符号表示，能用两个点表示一条直线是本节课的逻辑基础，因此，本节课的思维发生的逻辑顺序应该是先探究基本事实“两点确定一条直线”，再探究用符号表示线段、射线、直线，最后探究其应用.基于上述思考，在这次市级教研活动中，笔者大胆创新，依据思维的发生、发展的逻辑顺序对教材进行加工和重组，从课堂反应来看，学生的认识清晰、理解深刻，思维发展更加自然.

3.创设情境，让思维的发展更加深刻.

思维发展是数学课堂教学的灵魂，它蕴含在知识的形成、发展过程中，离不开特定的问题情境.创设好的问题情境是思维发展的前提，它能起到思维的定向、激发作用.什么是好的问题情境？裴光亚先生作出了精辟的论述：愤、悱是对“问题情境”的恰当描述.愤，就是想求明白而感到困难；悱，就是想说出又说不明白.它不只是“问题”，在问题的背后，还有一种内在需求，一种学生主动探究的愿望.好的数学情境应具有三个特征：（1）应该是学生熟悉的；（2）应该是简明的；（3）应必然引向数学的本质.本节课注重对问题情境的精心设计，开始阶段让学生画出“线段、射线和直线”，化抽象为具体；接着请学生操作、探究，积累基本活动经验，感悟基本事实“两点确定一条直线”，感受数学与生活及其他学科的联系，体验数学思想；其次，以数线段为问题情境，探究数射线和直线的方法，渗透化繁为简、由特殊到一般、归纳类比的思想方法；最后以问题情境进行小结，让学生辨析概念的异同，谈收获与体会，让思维有了载体，方法有了灵魂.

4.开发习题，让思维的形成更加深刻.

著名的数学教育家波利亚指出，拿一个有意义而又不复杂的题目帮助学生挖掘问题的各个方面，使得通过这道题就好像通过一道门户，把学生引入一个完整的领域.教材中的一些例题或习题往往具有这样的功能，需要教师对这些题目加以深入思考与研究，发挥题目的真正价值.如本节教材中“议一议”的目的在于引导学生掌握认识图形的一种技能——从较复杂的图形中分解出基本图形，培养学生的读图能力，该习题的编制目标比较单一、内容没有梯度，考虑到数学学习的目的，不仅是巩固知识，应用知识，更重要的是让学生自主探究，培养学生的问题意识，发展学生发现问题、提出问题、分析问题和解决问题的能力，因此，笔者对该习题进行了创新设计，设计成以数线段为问题情境，在学生给出数以A为端点的线段方案的基础上，让学生尝试提出问题，通过新问题的分析与解决，得到数射线和直线的方法、经验和结论，学生经历类比、归纳、猜想，最终提炼出一些本质规律方面的新知，达到进一步完善解题经验的效果，从而提升学生的解题能力.在平时教学中，要结合学情进行适当变式、扩充、拓展与延伸，从一个问题到一类问题，逐步寻求发现解题的内在规律，培养、锻炼学生科学的思维方法，获得举一反三、触类旁通的本领，提升学生的数学综合素养.

应该说，这节课努力以生为本，以问题为主线，以发展学生思维能力为目标，遵循知识螺旋上升的原则，大胆创新教学设计，通过创设丰富多彩的情境，激发学生思维；通过开展数学探究活动，调动学生思维；通过对课本习题的开发，深化学生思维.整节课，学生的思维发展更加自然、丰盈和深刻，真正达到了“年年岁岁课相似，岁岁年年课不同”的效果.

1.中华人民共和国教育部制订.义务教育数学课程标准（2011年版）［S］.北京：北京师范大学出版社，2012.

2.杨裕前，董林伟.义务教育课程标准实验教科书数学（七年级上册）［M］.江苏：江苏科技出版社.

3.黄玉华，陈德前.培养问题意识推开问题大门——“线段、射线、直线（第1课时）”的教学实录及其点评［J］.中学数学（下），2014（3）.