一道中考数学模拟试题的证明与拓展
2017-03-10北京教育学院朝阳分院白雪峰
☉北京教育学院朝阳分院 白雪峰
一道中考数学模拟试题的证明与拓展
☉北京教育学院朝阳分院 白雪峰
(北京市东城区2015—2016学年第二学期统一练习(一),初三数学第28题)如图1,等边△ABC,其边长为1,D是BC的中点,点E、F分别位于边AB、AC上,且∠EDF= 120°.

图1
(1)直接写出DE与DF的数量关系.
(2)若BE、DE、CF能围成一个三角形,求出这个三角形的最大内角(要求:写出思路,画出图形,直接给出结果即可).
(3)思考:AE+AF的长是否为定值?如果是,请求出该值;如果不是,请说明理由.
说明:名曰统一练习,其实就是初三数学第一次模拟考试.本题是一道平面几何压轴题,具有一定的开放度和探究性,通过本题不仅可以检测学生几何学习的基础知识、基本技能,特别是对几何基本图形变换的理解和掌握程度,对基本思想和基本活动经验的感悟和认知水平,同时,也考查了学生在几何学习过程中的直观想象素养和学习探究能力.本文将对每一个问都给出详细求解过程,以展示数学思维过程的严密性.
一、模拟试题的求解
(1)解:猜想DE=DF.
证法1:如图2,连接AD,则AD为∠BAC的平分线.
过点D作DH⊥AC于H,DG⊥AB于G.
由∠EDF=120°,得∠FDC+∠EDB=180°-120°=60°.∠HFD=∠FCD+∠FDC=60°+∠FDC,①
∠GED=∠BED=180°-∠B-∠EDB=120°-∠EDB.②①-②得:∠HFD-∠GED=-60°+(∠FDC+∠EDB)= 60°-60°=0.
所以∠HFD=∠GED.
则Rt△DGE≌Rt△DHF.
则DE=DF.
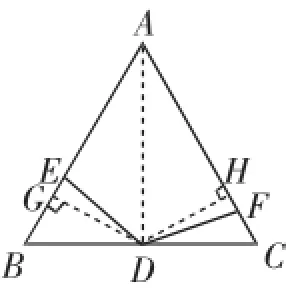
图2
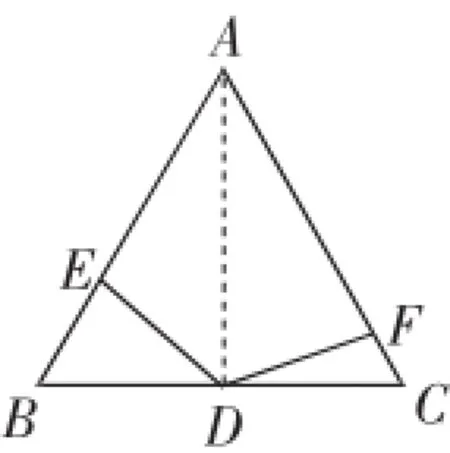
图3
证法2:如图3,连接AD.
∠EAF+∠EDF=60°+120°=180°.
所以A、E、D、F四点共圆.
AD为∠BAC的平分线.
则∠EAD=∠FAD.
则DE=DF.
说明:证法1利用构造全等三角形的方法证明线段相等,过程冗长、繁杂;证法2利用四点共圆的知识证明圆中的弦DE=DF,过程直观、简洁.在第(2)和(3)问中,我们将直接应用A、E、D、F四点共圆及∠FDC+∠EDB= 60°这两个结论解决问题.
(2)解:如图4,延长FD到点K,使DK=DF,连接BK、EK.
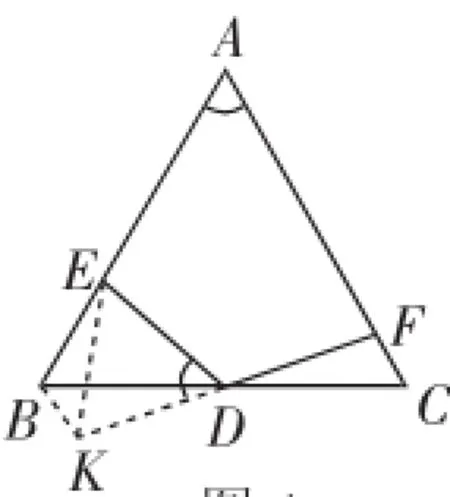
图4
由∠BDK=∠CDF,D为BC的中点,得△BDK≌△CDF.
则BK=CF,∠KBD=∠FCD.
∠EDK=∠EDB+∠BDK=∠EDB+∠FDC=60°.又ED= DF=DK,则△DEK为等边三角形,则EK=DE.
由BE、CF、DE为边围成的△EKB中,∠EBK最大,
此时,∠EBK=∠EBD+∠KBD=60°+60°=120°.
说明:如图4,四边形EBKD中,∠EDK=60°,∠EBK= 120°,∠EDK+∠EBK=180°,E、B、K、D四点共圆,即四边形EBKD为圆内接四边形,与四边形EDFA有相同的特殊性,∠EDK=∠EAF=60°,∠EBK=∠EDF=120°,DE=DK,DE=DF.如果将等边△ABC推广到一般的等腰三角形(△ABC中,AB=AC),上述这些特征依然成立,所以它们都是图形运动变化过程中的不变量,也是此题的本质特征.而求出由BE、DE、CF能围出的三角形的最大内角,只是在等边三角形中成立的特殊性情况,在一般等腰三角形中不存在这种情况.因此,笔者在拓展问题中,把由线段BE、CF、DE、DF能否围成有一组邻边相等的四边形,且相等邻边所夹的角等于原等腰三角形的顶角作为拓展问题.
(3)解法1:如图5,在CA上截取FM=BE.

图5
由A、E、D、F四点共圆,得∠BED=∠MFD.又DE=DF,则△BED≌△MFD.则∠FMD=∠EBD=60°,
则∠A=∠FMD.则DM∥AB.
AE+AF=AB-BE+AC-CF=2AB-(BE+CF)=
解法2:如图2,由(1)证法1证得:Rt△DGE≌Rt△DHF,GE=HF.
二、模拟试题的拓展
等边三角形是一种特殊的等腰三角形,类比于其他特殊的等腰三角形,又会产生怎样的结论呢?首先我们来看等腰直角三角形.
拓展1:把等边三角形变化为等腰直角三角形.
如图6,已知在△ABC中,∠BAC=90°,AB=AC,点D是BC的中点,点E、F分别在边AB、AC上,且∠EDF=90°.求证:

图6
(1)DE=DF;
(2)线段BE、DE、DF和CF能围成一组邻边相等且相等邻边所夹的角等于90°的圆内接四边形;
证明:(1)∠EAF+∠EDF=90°+90°=180°,所以A、E、D、F四点共圆.
连接AD,则AD为∠BAC的平分线,即∠BAD=∠CAD=45°.
则DE=DF.
(2)如图7,延长FD到K,使DK=DF,连接BK.
由∠FDC=∠BDK,DC=DB,DF=DK,得△FDC≌△BDK.
所以∠FCD=∠KBD=45°,FC=BK.
由∠EDF=90°,得∠EDB+∠FDC=90°,则∠EDB+∠KDB=90°,即∠EDK=90°.
则E、B、K、D四点共圆,且DE=DK=DF,∠EDK=∠BAC=90°.

图7
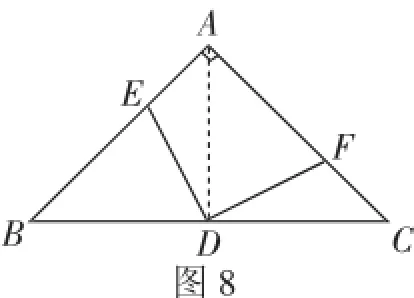
图8
(3)如图8,连接AD.
由(1)知∠BAD=45°.
所以AD=DC=BD.
因为A、E、D、F四点共圆,注意到DE=DF,则△AED≌△CFD.
则CF=AE.
拓展2:把等边三角形变化为一般的等腰三角形.
如图9,在等腰△ABC中,AB=AC,∠BAC=α,D是BC的中点,点E、F分别在边AB、AC上,且∠EDF=180°-α.求证:
(1)DE=DF;
(2)线段BE、DE、DF和CF能围成一组邻边相等且相等邻边所夹的角等于α的圆内接四边形;
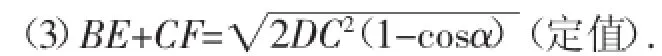
证明:(1)证明方法与原题和拓展1相同,略.
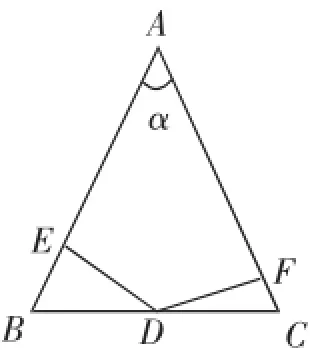
图9

图10
(2)如图10,延长FD到点K,使DK=DF,连接BK.
由∠FDC=∠KDB,DB=DC,DK=DF,得△BDK≌△CDF.
所以BK=CF,∠DBK=∠DCF.则∠EBK=∠EBD+∠DBK=∠EBD+∠DCF=180°-∠BAC.
因为∠EDF=180°-∠BAC,所以∠EDB+∠FDC=∠BAC.
则∠EDB+∠BDK=∠BAC.
所以∠EDK=∠BAC.
所以E、B、K、D四点共圆.
所以由线段BE、DE、DF和CF围成的四边形是圆内接四边形,且DE=DK,∠EDK=∠BAC=α.
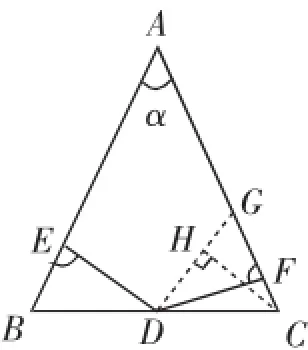
图11
(3)如图11,在AF上截取FG= BE,连接DG,过点C作CH⊥DG于H.
因为A、E、D、F四点共圆,所以∠BED=∠GFD.又DE=DF,BE=GF,则△BED≌△GFD.
所以BD=DG=DC,∠BDE=∠GDF.
∠CDG=∠CDF+∠FDG=∠CDF+∠BDE=180°-∠EDF=α.
在Rt△DHC中,DH=DC·cosα.
则HG=DG-DH=DC-DC·cosα.
CG2-HG2=DC2-DH2,即CG2-DC2(1-cosα)2=DC2-DC2·cos2α.
所以CG2=DC2·cos2α+DC2-2DC2·cosα+DC2-DC2· cos2α=2DC2(1-cosα).
